Теорема Лагранжа: следствия

1. Условие постоянства функции на отрезке

Пусть функция f (x) непрерывна на отрезке [a, b] и дифференцируема в каждой точке интервала (a, b).

Теорема Лагранжа: следствия

2. Условие равенства производных функций

Пусть функции f (x) и g (x) непрерывны на отрезке [a, b] и дифференцируемы в каждой точке интервала (a, b),

Теорема Лагранжа: следствия

3. Условие монотонности функции

Пусть функция f (x) непрерывна на отрезке [a, b] и дифференцируема в каждой точке интервала (a, b).

Тогда если на этом интервале f (x) 0, то функция f (x) строго монотонно возрастает на интервале (a, b),

убывает на интервале

Выпуклость и вогнутость (графика) функции

Определение 1:

Если п производных функции f (x) являются непрерывными функциями, то функцию f (x) называют п раз непрерывно дифференцируемой функцией.

Выпуклость и вогнутость (графика) функции

Определение 2:

Непрерывно дифференцируемая функция f (x) называется

лежат не выше касательной, проведённой к нему в любой точке c [a,b].

Выпуклость и вогнутость (графика) функции

Определение 3:

Непрерывно дифференцируемая функция f (x) называется вогнутой (или выпуклой вниз) на интервале (a, b), если

лежат не ниже касательной, проведённой к нему в любой точке c [a,b].

Выпуклость и вогнутость (графика) функции

Теорема (достаточное условие выпуклости):

Пусть функция f (x) – дважды непрерывно дифференцируемая на интервале (a,b). Если для x (a,b) выполнено

Точки перегиба (графика) функции

Определение:

Точка x0 называется точкой перегиба функции f (x), если

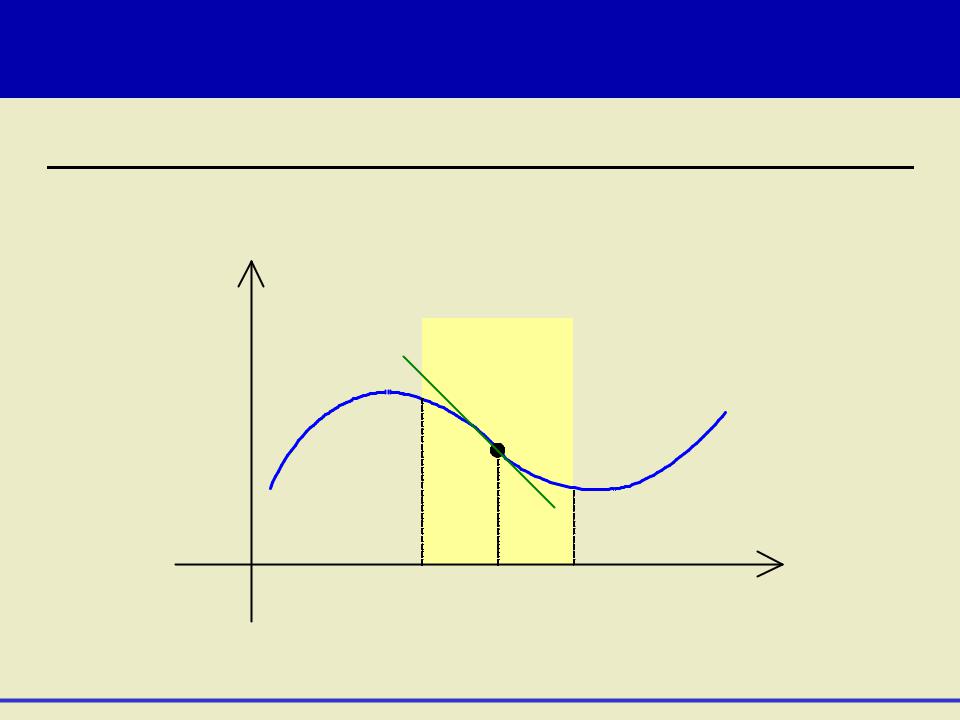
Точки перегиба (графика) функции

Пример: