
- •1.Що таке статистика
- •Статистичні
- •За глибиною
- •За атрибутивною ознакою
- •1. Абсолютні і відносні величини
- •Загальні умови правильного використання абсолютних і відносних величин
- •2. Середні величини
- •1.Середня варіаційних рядів
- •2. Структурні середні
- •3. Показники варіації
- •4. Середня та дисперсія альтернативної ознаки
- •2. Методика проведення дисперсійного аналізу
- •3. Кореляційно-регресійний метод
- •4. Непараметричні методи вивчення
- •5. Рангова кореляція
- •Динаміка реалізації овочів на ринках міста *
- •Динаміка чисельності учнів
- •2. Характеристика
- •3. Показники аналізу рядів динаміки
- •4. Порівняльний аналіз рядів динаміки
- •5. Методи виявлення основної тенденції
- •Динаміка обсягу вантажних перевезень
- •Допоміжна розрахункова таблиця
- •Індекси
- •4. Середні індекси
- •5. Індекси середніх величин
3. Показники аналізу рядів динаміки
Найважливішим завданням динамічних рядів є дослідження розвитку явищ. Ось чому при аналізі таких рядів важливо простежити за напрямком і розміром змін рівнів ряду у часі. З цією метою для динамічних рядів розраховують показники абсолютної і відносної зміни їх рівнів. У залежності від вибору бази порівняння ці показники можуть бути обчислені як ланцюгові та як базисні.
За ланцюговою
схемою
ведеться зіставлення кожного рівня
ряду динаміки –
![]() з рівнем попереднього періоду (або
моменту) часу –
з рівнем попереднього періоду (або
моменту) часу –
![]() .
.
За базисною
схемою кожний
рівень ряду динаміки (![]() )
зіставляють з одним рівнем, який приймають
за базу порівняння. Частіше за все це
буває перший (початковий) рівень ряду
–
)
зіставляють з одним рівнем, який приймають
за базу порівняння. Частіше за все це
буває перший (початковий) рівень ряду
–![]() ,
але може бути і рівень будь-якого іншого
попереднього періоду (або моменту) часу,
що знаходиться поза рядом –
,
але може бути і рівень будь-якого іншого
попереднього періоду (або моменту) часу,
що знаходиться поза рядом –
![]() 69.
69.
Між ланцюговими і базисними показниками існує безпосередній зв’язок, що дає змогу при необхідності переходити від одних до других, тобто від ланцюгових показників до базисних і навпаки. Цей взаємозв’язок забезпечує можливість відшукувати невідомі показники, урізноманітнює методи розрахунку середніх значень показників аналізу ряду динаміки.
Аналіз динамічного ряду починають зі статистичного показника, який характеризує абсолютну зміну рівнів ряду – абсолютного приросту.
Абсолютний приріст (Δ) показує, на скільки одиниць один рівень ряду більше (+) або менше (-) другого. Отже, для його розрахунку необхідно знайти різницю між порівнюваними рівнями ряду динаміки:
- ланцюговий
абсолютний
приріст:
![]() ;
(68)
;
(68)
- базисний
абсолютний приріст:
![]() .
(69)
.
(69)
Важливо знати, розуміти і широко використовувати у розрахунках взаємозв’язок між ланцюговими і базисними абсолютними приростами. Цей взаємозв’язок полягає у тому, що сума ланцюгових приростів дорівнює базисному за той же відрізок часу:
![]() (70-а)
(70-а)
або різниця сусідніх базисних дає відповідний ланцюговий:
(
![]() -
-
![]() )
=
)
=
![]() (70-б)
(70-б)
Покажемо цей взаємозв’язок у загальному
вигляді на прикладі розрахункових
формул перших двох абсолютних приростів.
Так, перший ланцюговий абсолютний
приріст знаходиться як різниця другого
і першого рівнів ряду динаміки:
![]() =
=
![]() ,
а другий ланцюговий абсолютний приріст
дорівнює різниці третього і другого
рівнів ряду:
,
а другий ланцюговий абсолютний приріст
дорівнює різниці третього і другого
рівнів ряду:
![]() =
=![]() ;
їх сума дає вираження: (
;
їх сума дає вираження: (![]() )
+ (
)
+ (![]() )
=
)
=
![]() ,
а це і є другий базисний абсолютний
приріст (
,
а це і є другий базисний абсолютний
приріст (![]() ).
І навпаки, якщо перший базисний абсолютний
приріст дорівнює:
).
І навпаки, якщо перший базисний абсолютний
приріст дорівнює:
![]() =
=
![]() ,
а другий базисний знаходиться як:
,
а другий базисний знаходиться як:
![]() =
=
![]() ,
то різниця між ними (другим і першим)
дає можливість отримати вираження: (
,
то різниця між ними (другим і першим)
дає можливість отримати вираження: (![]() )
- (
)
- (![]() )
=
)
=
![]() ,
яке й виступає засобом розрахунку
другого ланцюгового абсолютного приросту
(
,
яке й виступає засобом розрахунку
другого ланцюгового абсолютного приросту
(![]() ).
).
Важливішим відносним показником аналізу ряду динаміки є коефіцієнт (темп) росту.
Коефіцієнт (темп)
росту (![]() )
показує, у
скільки разів один рівень ряду динаміки
більше або менше за другий.
Отже, для його розрахунку необхідно
знайти відношення двох рівнів ряду
динаміки:
)
показує, у
скільки разів один рівень ряду динаміки
більше або менше за другий.
Отже, для його розрахунку необхідно
знайти відношення двох рівнів ряду
динаміки:
- ланцюговий
коефіцієнт
росту:
![]()
![]() ;
(71)
;
(71)
- базисний
коефіцієнт росту:
![]()
![]() .
(72)
.
(72)
Через множення цих коефіцієнтів на 100% отримують відповідні темпи росту:
- ланцюговий
темп росту:
![]() =
(
=
(
![]() )
· 100; (73)
)
· 100; (73)
- базисний
темп росту:
![]() =
(
=
(
![]() )
· 100. (74)
)
· 100. (74)
Між ланцюговими і базисними коефіцієнтами (темпами) росту також існує взаємозв’язок, а саме: добуток послідовних ланцюгових відносних показників динаміки дорівнює заключному базисному або частка від ділення двох сусідніх базисних дає відповідний ланцюговий коефіцієнт (темп) росту:
![]() (75-а)
(75-а)
або
![]() .
(75-б)
.
(75-б)
Проілюструємо зазначений у наведених
формулах взаємозв’язок у загальному
виді на прикладі перших двох коефіцієнтів
росту. Перший ланцюговий коефіцієнт
росту дорівнює:
![]() ,
а другий –
,
а другий –
![]() .
Через добуток цих двох ланцюгових
коефіцієнтів росту отримують другий
базисний коефіцієнт росту:
.
Через добуток цих двох ланцюгових
коефіцієнтів росту отримують другий
базисний коефіцієнт росту:
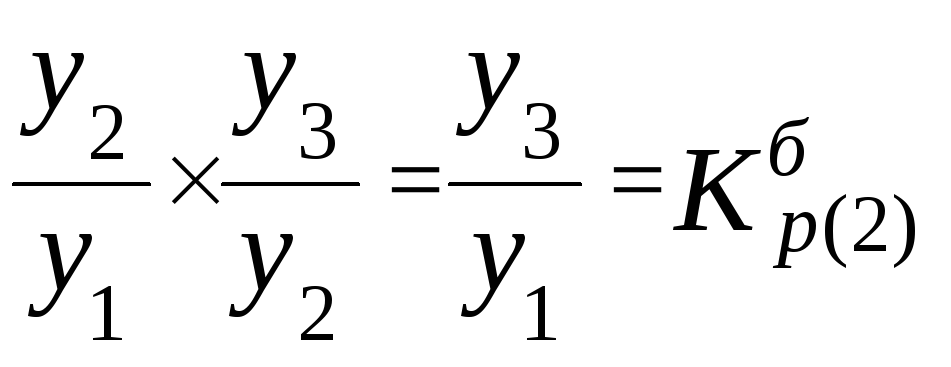 .
Якщо ж два перших базисних коефіцієнта
росту співвіднести між собою (розділити
другий на перший), то утворюється другий
ланцюговий коефіцієнт росту:
.
Якщо ж два перших базисних коефіцієнта
росту співвіднести між собою (розділити
другий на перший), то утворюється другий
ланцюговий коефіцієнт росту:
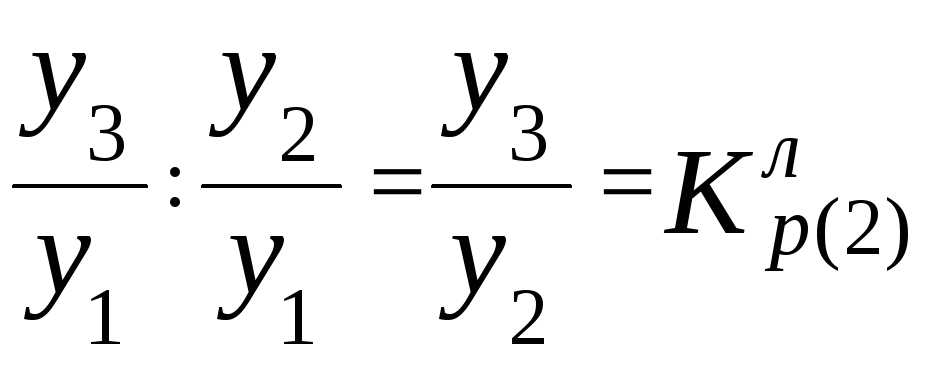 .
.
Розрахунок і аналіз темпів росту обов’язково припускає встановлення темпів приросту.
Темп приросту
(![]() )
показує, на
скільки % один рівень ряду динаміки
більше (+) або менше (-) за другий.
Оскільки базу порівняння при розрахунку
темпів росту завжди приймають за 100%, то
для розрахунку темпу приросту достатньо
із темпу росту відняти 100%:
)
показує, на
скільки % один рівень ряду динаміки
більше (+) або менше (-) за другий.
Оскільки базу порівняння при розрахунку
темпів росту завжди приймають за 100%, то
для розрахунку темпу приросту достатньо
із темпу росту відняти 100%:
![]() =
=
![]() – 100%. (76)
– 100%. (76)
Темп приросту, відповідно, як і темп росту, може бути обчислений за ланцюговою та базисною схемою. Підстановка у формулу (76) розрахункових формул темпів росту (ланцюгового або базисного) і наступні перетворення дають змогу отримати прямі формули розрахунку темпів приросту:
-
ланцюговий
темп приросту:
![]() =
=
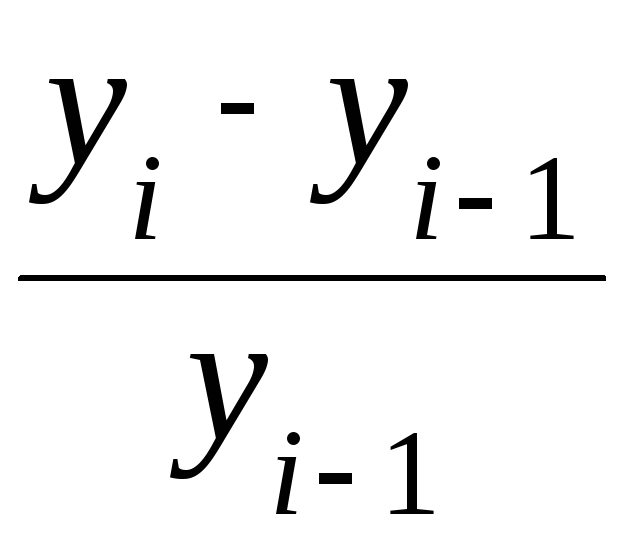 . 100; (77)
. 100; (77)
-
базисний
темп приросту:
![]() =
=
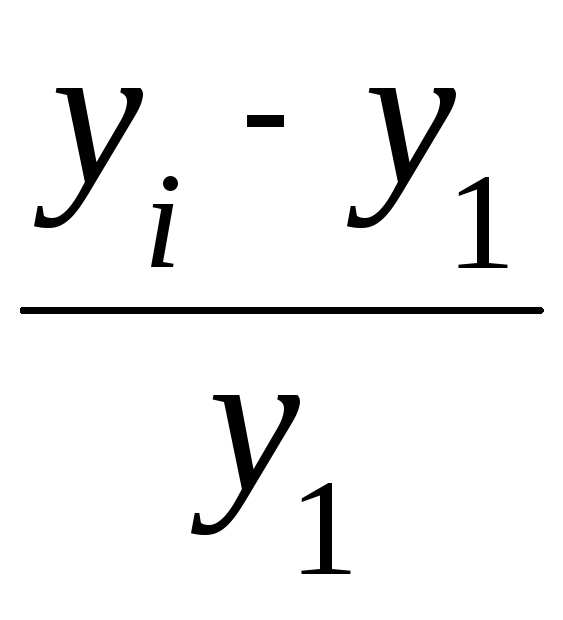 . 100. (78)
. 100. (78)
Як бачимо, прямі формули розрахунку темпів приросту (ланцюгового або базисного) – це відношення відповідного абсолютного приросту (ланцюгового чи базисного) до рівня ряду динаміки (попереднього або першого), у порівнянні з яким обчислено кожний абсолютний приріст.
На відміну від
вище розглянутих показників (абсолютних
приростів і темпів росту) ланцюгові і
базисні темпи приросту безпосередньо
не взаємопов’язані. Але поєднання
окремих елементів розрахункових формул
ланцюгового та базисного темпів приросту
дає новий, цікавий в аналітичному плані,
показник. Він зветься “темп
нарощування
–
![]() ”
і розраховується як відношення ланцюгового
абсолютного приросту (
”
і розраховується як відношення ланцюгового
абсолютного приросту (![]() )
до базисного (звичайно першого) рівня
ряду динаміки (
)
до базисного (звичайно першого) рівня
ряду динаміки (![]() ):
):
![]() =
(
=
(![]() :
:
![]() )
· 100 . (79)
)
· 100 . (79)
Іноді темпи росту і темпи приросту самі по собі не дають повної уяви про дійсний розвиток явища. Так, за однаковими темпами приросту двох показників можуть ховатися надто відмінні один від одного абсолютні значення цих приростів. Це може мати місце у випадку, коли відносні показники динаміки обчислені у порівнянні з різними абсолютними базовими значеннями. Так, наприклад, якщо мова йде про підвищення пенсії за віком на 10%, то абсолютний приріст загальних трудових пенсій, які складають 142 грн., буде дорівнювати 14,2 грн. У той же час таке ж саме 10-відсоткове підвищення пенсії за віком наукових працівників, яка, наприклад, може складати 500 грн., призведе до її збільшення на 50 грн.
Раніше вже розглядалась і обгрунтовувалась необхідність тісного взаємозв’язку при аналізі абсолютних і відносних величин70. У дослідженні динамічних рядів, як бачимо, це особливо доцільно. Ось чому аналіз рядів динаміки доповнюють ще одним показником, який установлює такий взаємозв’язок.
Абсолютне значення
1% приросту
(![]() )
вказує на
абсолютну величину показника, що
припадає на кожний відсоток приросту.
Виражають показник у тих же одиницях,
що і рівні ряду динаміки і розраховують
як співвідношення абсолютного приросту
і темпу приросту:
)
вказує на
абсолютну величину показника, що
припадає на кожний відсоток приросту.
Виражають показник у тих же одиницях,
що і рівні ряду динаміки і розраховують
як співвідношення абсолютного приросту
і темпу приросту:
![]() =
=
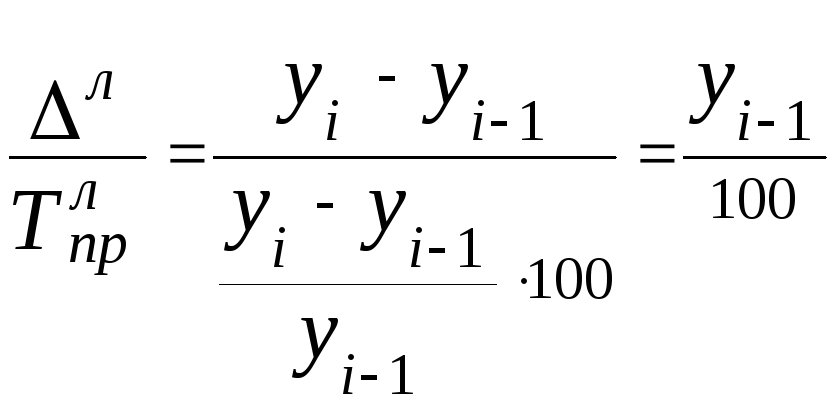 = 0,01
= 0,01![]() .
(80)
.
(80)
Цей показник має
економічний сенс тільки за ланцюговою
системою, оскільки усі базисні його
значення однакові між собою – для
будь-якого року
![]() буде
дорівнювати 0,01 у1,
тобто одній сотій першого рівня ряду
динаміки.
буде
дорівнювати 0,01 у1,
тобто одній сотій першого рівня ряду
динаміки.
СЕРЕДНІ ПОКАЗНИКИ АНАЛІЗУ РЯДІВ ДИНАМІКИ
Для отримання узагальнених характеристик часових рядів обчислюють середні значення розглянутих показників аналізу ряду.
Середній абсолютний приріст показує, на скільки у середньому приростав за одиницю часового відрізку показник, що розглядається у динаміці. Його обчислюють за формулою середньої арифметичної простої із ланцюгових абсолютних приростів:
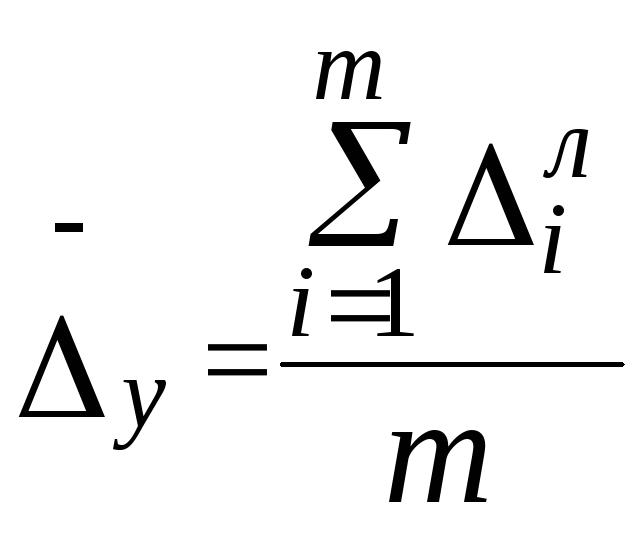 ,
(81)
,
(81)
де
![]() – ланцюгові абсолютні прирости;
– ланцюгові абсолютні прирости;
m – число ланцюгових абсолютних приростів (нагадаємо, що воно на одиницю менше числа рівнів (n) у ряду динаміки, тобто m = n - 1).
Беручи до уваги взаємозв’язок ланцюгових і базисних абсолютних приростів71, формула (81) може бути записана таким чином:
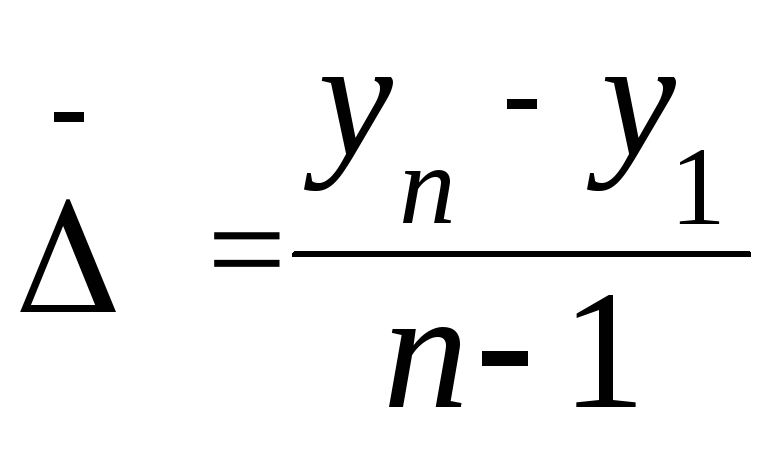 ,
(82)
,
(82)
де
(![]() )
– базисний абсолютний приріст за весь
період;
)
– базисний абсолютний приріст за весь
період;
(n – 1) – число проміжків між датами у ряду динаміки з „n” рівнями.
Обчислимо величину середньорічного абсолютного приросту за даними табл. 8.1., використовуючи кожну з розглянутих формул:
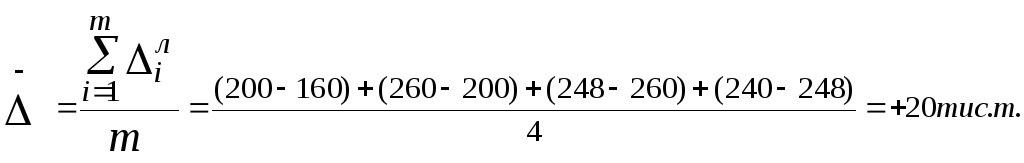
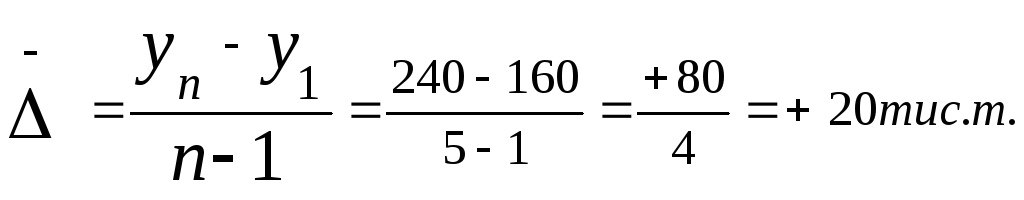
Таким чином, реалізація овочів на ринках міста протягом останніх п’яти років щорічно приростала в середньому на 20 тис. т.
Середній коефіцієнт (темп) росту показує, у скільки разів у середньому змінювався рівень ряду динаміки за одиницю часового відрізку. Його розраховують із ланцюгових коефіцієнтів росту за формулою середньої геометричної:
![]() =
=
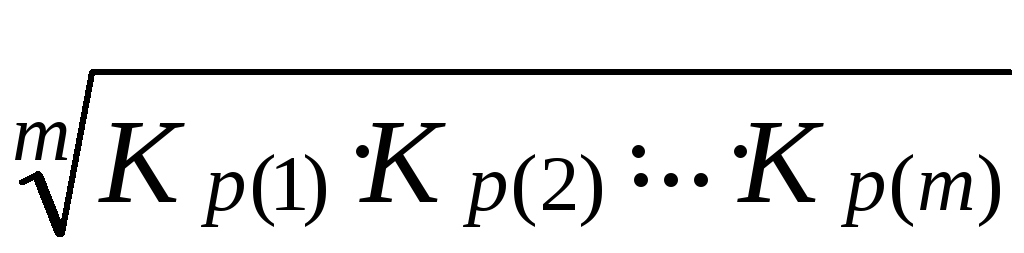 , (83)
, (83)
де m – число ланцюгових коефіцієнтів росту, яке дорівнює числу проміжків між “n” датами (m = n – 1).
Якщо взяти до уваги взаємозв’язок ланцюгових і базисних коефіцієнтів (темпів) росту72, то розрахунок середнього коефіцієнта (темпу) росту можна провести за формулою:
![]() =
=
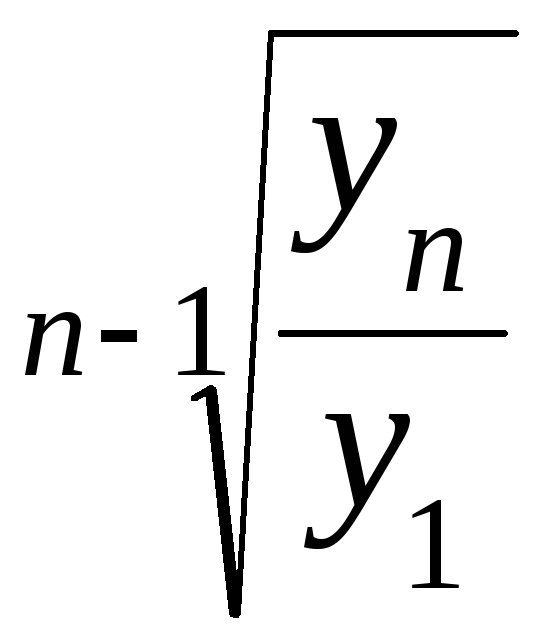 ,
(84) де
,
(84) де
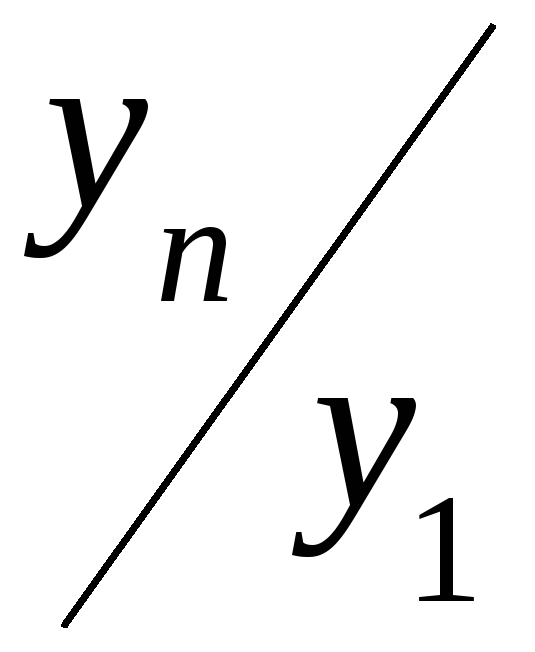 – базисний коефіцієнт росту за весь
період;
– базисний коефіцієнт росту за весь
період;
n – число рівнів ряду (число дат);
n -1 – число проміжків між датами.
Проілюструємо використання наведених формул на тому ж прикладі (табл.8.1):
![]() =
=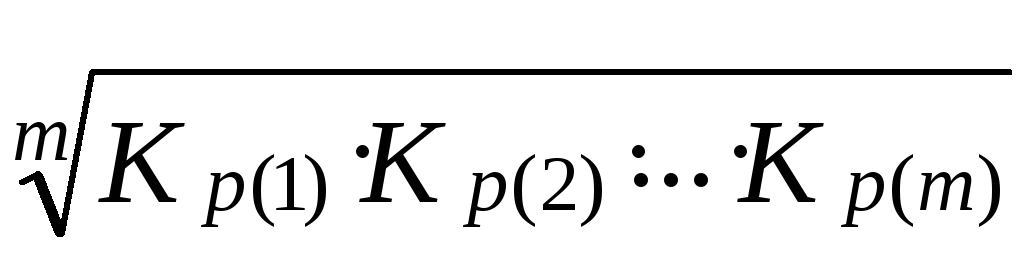 =
=![]() =
=![]() =
=
=
=![]() = 1,107 або 110,7%, тобто протягом 1998-2002 років
реалізація овочів на ринках міста
щорічно збільшувалась у середньому в
1,107 разів або на 10,7% (110,7 - 100). Такий же
результат буде отримано, якщо розрахунок
шуканої величини провести за формулою
(84):
= 1,107 або 110,7%, тобто протягом 1998-2002 років
реалізація овочів на ринках міста
щорічно збільшувалась у середньому в
1,107 разів або на 10,7% (110,7 - 100). Такий же
результат буде отримано, якщо розрахунок
шуканої величини провести за формулою
(84):
![]() =
=
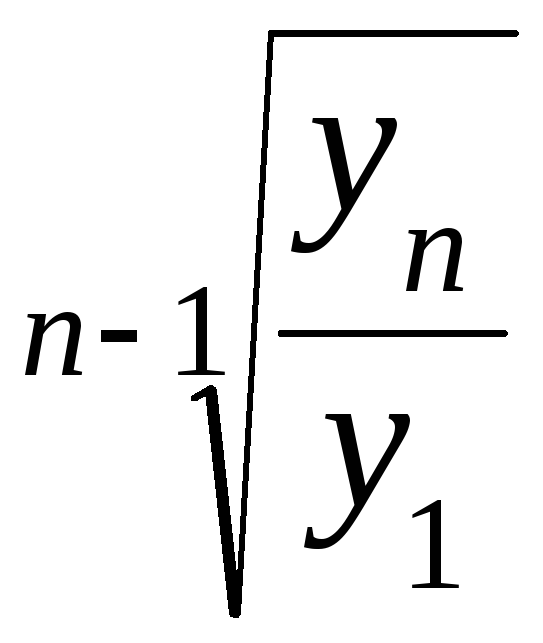 =
=
![]() =
=
![]() = 1,107 або 110,7%.
= 1,107 або 110,7%.
Середній коефіцієнт (темп) приросту показує, на скільки відсотків (%) у середньому приростав за одиницю часового відрізку показник, що розглядався у динаміці. Він знаходиться єдиним способом: як різниця середнього коефіцієнта (темпу) росту і одиниці (100%):
![]() =
=
![]() -
1, (85)
-
1, (85)
або
![]() =
=
![]() -
100 . (86)
-
100 . (86)
Обчислимо середній темп приросту за даними табл. 8.2. Як випливає із наведених формул, перш за все треба визначити середній коефіцієнт росту:
![]() =
=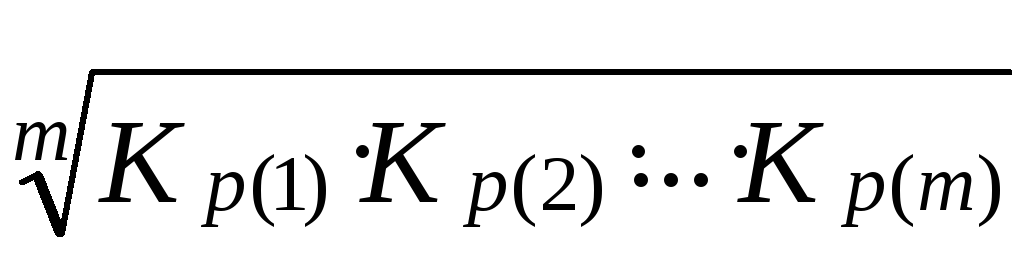 =
=![]() =
=![]() =
=
=
=![]() = 0,964 або 96,4%.
= 0,964 або 96,4%.
Тоді шуканий показник становитиме:
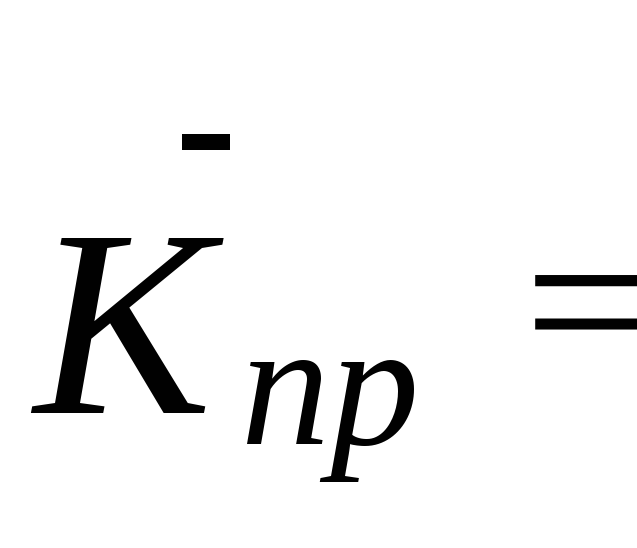
![]() -
1= 0,964 -1= - 0,036 або
-
1= 0,964 -1= - 0,036 або
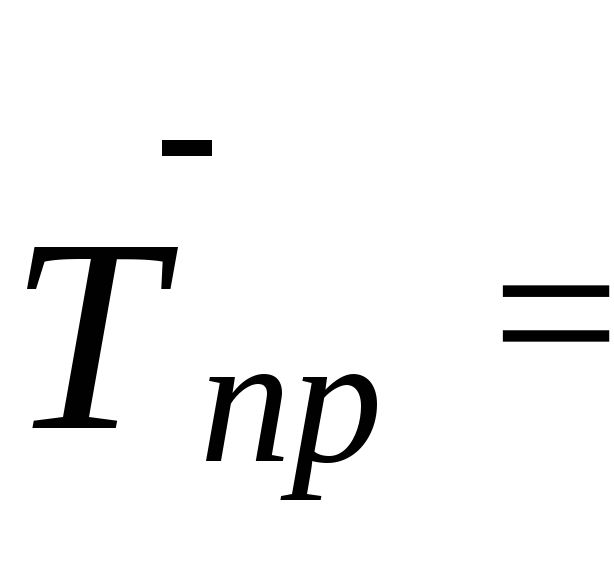
![]() -100=96,4-100=
- 3,6%, тобто за розглянутий період щорічно
чисельність учнів у загальноосвітніх
школах регіону знижувалась у середньому
на 3,6%.
-100=96,4-100=
- 3,6%, тобто за розглянутий період щорічно
чисельність учнів у загальноосвітніх
школах регіону знижувалась у середньому
на 3,6%.
Середнє абсолютне значення 1% приросту установлює середню абсолютну величину показника, що припадає на кожний відсоток приросту в межах періоду, що аналізують. Розрахунок здійснюють за формулою середньої арифметичної простої:
![]() =
=
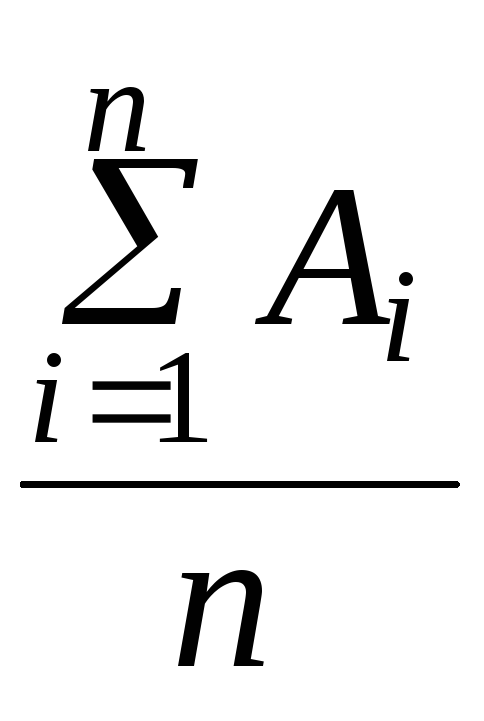
![]() , (87)
, (87)
де
![]() -
ланцюгові показники абсолютного змісту
1% приросту;
-
ланцюгові показники абсолютного змісту
1% приросту;
n - число усереднених показників.
Розрахуємо даний показник на прикладі табл. 8.1:

Таким чином, кожний відсоток приросту реалізації овочів на ринках міста був у середньому рівнозначний приросту реалізації на 2,17 тис. т.
