Динамика твердого тела

Динамика твердого тела. Поступательное и вращательное движения твердого тела. Момент сил. Момент инерции. Моменты инерции тел правильной геометрической формы. Уравнение движения твердого тела. Кинетическая энергия твердого тела, которое вращается вокруг оси. Центр масс, центр инерции, центр тяжести. Основной закон движения вращательного движения. Момент импульса. Закон сохранения момента импульса

До сих пор мы рассматривали движения тел, которые можно было представить как материальные точки. Теперь перейдем к изучению движения таких тел, которые имеют существенную протяженность. Твердое тело – это неизменяемая система материальных точек, при любых движениях которой взаимные расстояния между частями системы остаются неизменными. Таким образом, твердое тело является абсолютно твердым, то есть недеформируемым.

Виды движения твердого тела.

Различают пять видов движения твердого тела:

1. поступательное – движение, при котором любая прямая, связанная с движущимся телом, будет перемещаться параллельно самой себе;

2. вращательное вокруг неподвижной оси – движение, при котором траектории материальных точек тела представляют собой окружности, центры которых лежат на одной и той же прямой, называемой осью вращения;

3. плоское движение;

4. движение вокруг неподвижной точки;

5. свободное движение.

Первые два вида движения являются основными. Остальные виды движения твердого тела можно представить как совокупность поступательного движения и вращательного движения вокруг неподвижной оси.

При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела для того, чтобы охарактеризовать полностью движение всего тела.

Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени. Кинематику вращательно движения мы уже изучили. Для динамического описания вращательного движения твердого тела необходимо ввести новые понятия: момент силы, момент импульса, момент инерции и получить закон вращательного движения.

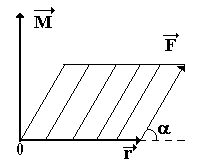
Моментом силы , относительно точки О называется векторное

произведение радиуса-вектора точки приложения силы относительно точки О на силу(см.рис):

(7.1)

Точка, относительно которой рассматривается момент, называется полюсом или началом. Из определения момента, на основании свойства векторного произведения, для суммы сил можно написать

(7.2)

Точку приложения силы можно переносить вдоль линии ее действия, момент силы при этом меняться не будет.

Если некоторая материальная точка имеет импульс и ее положение относительно точки О задано радиус-вектором,то моментом импульса называют векторное произведение радиус-вектораотносительно точки О на импульс материальной точки:

(7.3)

Найдем связь между введенными величинами. Продифференцируем по времени момент импульса:

(7.4)

Так как , а, то (7.4) можно переписать в виде

(7.5)

Первое слагаемое в правой части равно нулю, т.к. параллельно,а второе слагаемое представляет собой момент силы. Тогда

(7.6)

Это уравнение называется уравнением моментов (закон вращательного движения), согласно которому производная по времени момента импульса материальной точки относительно неподвижного начала равна моменту силы, действующей на это тело относительно того же начала.

Сравнивая с основным законом динамики материальной точки:

видим, что в динамике твердого тела аналогом силы является момент силы, а аналогом импульса является момент импульса.

Обобщим полученное соотношение (7.6) на случай произвольной системы материальных точек.

Моментом импульса системы материальных точек относительно некоторого начала называется векторная сумма импульсов материальных точек, входящих в систему, относительно того же начала:

Аналогично для моментов сил:

Под в этом соотношении следует понимать момент всех сил как внутренних, так и внешних. Однако, используя третий закон Ньютона можно показать, что моменты внутренних сил попарно компенсируются. Таким образом, для системы материальных точек, будем иметь:

(7.7)

то есть производная по времени от момента импульса системы материальных точек относительно неподвижного начала равна геометрической сумме моментов всех внешних сил относительно того же начала.

Из уравнения (7.7) видно, что если , то . Если момент внешних сил относительно неподвижного начала О равен нулю, то момент импульса системы относительно того же начала остается постоянным во времени.Это утверждение называется законом сохранения момента импульса.

Это может быть в трех случаях:

(система замкнута)

коллинеарный (плечо силы равно нулю)

(радиус-вектор точки приложения силы равен нулю).

В отличие от закона сохранения импульса, закон сохранения момента импульса может выполняться и в некоторых незамкнутых системах тел.

Уравнение моментов при вращении тела вокруг неподвижной оси

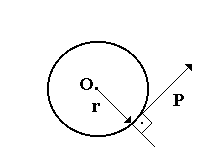
Рассмотрим вращательное движение твердого тела вокруг неподвижной оси (см.рис.). Пусть материальная точка вращается по окружности, тогда момент импульса относительно оси вращения и следовательно.

Выразим линейную скорость через угловую и подставим в выражение для момента импульса:

Если вокруг оси О вращается система материальных точек с одной и той же угловой скоростью, то суммарный момент импульса будет иметь вид:

(7.8)

где .

Величина, равная сумме произведений элементарных масс материальных точек на квадраты расстояний их до оси вращения называется моментом инерции системы относительно этой оси.

В случае сплошного тела, момент инерции относительно заданной оси равен интегралу по всей массе тела от произведения элементарной массы на квадрат ее расстояния до оси вращения:

Подставим в (7.8), получим, что момент импульса относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость вращения тела:

(7.9)

Сравнивая с определением импульса тела , видим, что в динамике твердого тела аналогом массы является момент инерции. При вращательном движении момент инерции характеризует инертные свойства тела.

Подставим (7.9) в уравнение моментов в проекции на ось и получим основное уравнение вращательного движения вокруг неподвижной оси:

(7.10)

М – момент внешних сил относительно оси вращения. Если рассматривается вращение твердого тела или системы материальных точек с неизменной конфигурацией вокруг неподвижной оси, момент инерции I остается неизменным и уравнение (7.10) принимает вид:

Учитывая, что угловое ускорение, запишем:

(7.11)

Произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.

Уравнение (7.11) представляет собой уравнение моментов при вращении твердого тела вокруг неподвижной оси. Оно является аналогом второго закона Ньютона в классической механике:

Если момент сил относительно оси вращения равен нулю, тогда согласно ,Отсюда(7.12)

Равенство (7.12) представляет собой закон сохранения момента импульса при вращении тела вокруг неподвижной оси: произведение момента инерции тела относительно оси вращения на угловую скорость вращения постоянно, если момент сил относительно оси вращения равен нулю. Это выражение аналогично закону сохранения импульса при поступательном движении тела: .