
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ КАФЕДРА ОБЩЕЙ ФИЗИКИ И ДИДАКТИКИ ФИЗИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для проведения лабораторных работ
по физике для студентов биологического факультета (механика и молекулярная физика)
Донецк 2015
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ КАФЕДРА ОБЩЕЙ ФИЗИКИ И ДИДАКТИКИ ФИЗИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ для проведения лабораторных работ
по физике для студентов биологического факультета (механика и молекулярная физика)
Рекомендовано к изданию решением Ученого совета физико-технического факультета ДонНУ (протокол № 1 от 21.09.14)
Донецк 2015
3
УДК 378. 147:52
Методические указания для проведения лабораторных работ по физике для студентов биологического факультета (механика и молекулярная физика) / Б.И. Бешевли, О.Б. Демина, Н.А. Куликова, А.Н. Семко / Под ред. А.Н. Семко – Донецк: ДонНУ, 2015. – 64 с.
Вметодических указаниях описаны лабораторные работы по механике и молекулярной физике в рамках рабочей программы курса физики для студентов биологического факультета университета. Инструкции к лабораторным работам содержат: цель работы, описание экспериментальной установки, порядок проведения эксперимента, правила записи и обработки результатов экспериментов, формулы для расчета погрешностей, вопросы для допуска и для сдачи лабораторных работ, теоретическую часть с выводом основных соотношений, приведенных в приложении. Вопросы для сдачи лабораторных работ ориентированы не только на конкретную лабораторную работу, а на тему, к которой относится данная лабораторная работа, и требуют знания фундаментальных законов физики.
Вметодических указаниях приведены правила выполнения и обработки результатов измерений, методы расчета погрешностей прямых и косвенных измерений, правила записи результатов измерений. Описаны приемы работы с основными измерительными инструментами и оценке приборной погрешности измерений. Дан график организации лабораторных занятий в рамках кредитномодульной системы.
Предназначены для студентов биологического факультета университета.
Ответственный за выпуск: доцент, к.ф.-м.н., А. Е. Зюбанов
Составители:
Б.И. Бешевли, О.Б. Демина, Н.А. Куликова, А.Н. Семко
Рецензент: д.ф.-м.н., профессор В. М. Юрченко
4
СОДЕРЖАНИЕ
1. Погрешности физических измерений............................................... |
5 |
1.1. Измерения и их погрешности...................................................... |
5 |
1.2. Приборная погрешность.............................................................. |
5 |
1.3. Погрешности прямых измерений................................................ |
6 |
1.4. Погрешности косвенных измерений........................................... |
7 |
1.5. Статистический метод учета погрешностей .............................. |
8 |
1.6. Метод границ.............................................................................. |
10 |
1.7. Обработка и запись результатов измерений........................... |
11 |
2. Измерительный практикум............................................................... |
13 |
2.1. Измерительные приборы........................................................... |
13 |
2.2. Определение объема и плотности тела правильной |
|
геометрической формы............................................................. |
17 |
2.3. Определение ускорения свободного падения при помощи |
|
математического маятника ....................................................... |
18 |
3. Механика.............................................................................................. |
21 |
3.1. Лабораторная работа № 1 «Изучение законов кинематики и |
|
динамики поступательного движения» .................................... |
21 |
3.2. Лабораторная работа № 2 «Проверка закона сохранения |
|
момента импульса»................................................................... |
28 |
3.3. Лабораторная работа № 3 «Проверка теоремы Гюйгенса – |
|
Штейнера».................................................................................. |
34 |
4. Молекулярная физика и термодинамика....................................... |
42 |
4.1. Лабораторная работа № 4 «Определение универсальной |
|
газовой постоянной».................................................................. |
42 |
4.2. Лабораторная работа № 5 «Определение показателя |
|
адиабаты воздуха».................................................................... |
48 |
4.3.Лабораторная работа № 6. «Определение коэффициента вязкости воздуха методом Пуазейля» (для получения
дополнительных баллов) .......................................................... |
54 |
5. Организация лабораторных работ.................................................. |
62 |
5.1. Правила выполнения и сдачи лабораторной работы ............. |
62 |
5.2. График проведения лабораторных работ................................ |
63 |
5
1. ПОГРЕШНОСТИ ФИЗИЧЕСКИХ ИЗМЕРЕНИЙ
1.1. Измерения и их погрешности
Измерением величины называется операция, в результате которой находится значение физической величины с помощью специальных технических средств измерения. Измерить физическую величину - это значит сравнить ее с величиной, принятой за единицу.
Различают прямые и косвенные измерения. Прямыми называют измерения, полученные непосредственно сравнением измеряемой величины с эталоном или отсчитанные по шкале прибора.
Косвенные измерения получают в результате расчета по формулам, в которые входят величины, определенные в результате прямых измерений.
При измерении величины всегда присутствует ошибка (погрешность), которую необходимо оценить. Ошибки, возникающие при измерении, делятся на: случайные, систематические и промахи.
Систематические ошибки сохраняют величину и знак при повторении опыта. Например, при измерении длины при помощи линейки с неправильной шкалой.
Промахи - это грубые ошибки, сделанные вследствие неверной записи показаний прибора, неправильно сделанного вычисления и т.д. Как правило, они существенно отличаются от средних значений измеряемой величины, поэтому они удаляются из таблицы измерений.
Случайные ошибки не повторяются от опыта к опыту, они могут быть вызваны дефектами аппаратуры, неточностью, допущенной экспериментатором. Для уменьшения случайных ошибок необходимо соблюдать такие правила:
а) при снятии показаний луч зрения должен быть перпендикулярен шкале измерительного прибора;
б) показания приборов необходимо округлять до значения, соответствующего ближайшему делению шкалы;
в) производить многократное повторение опыта.
Случайные погрешности непредсказуемым образом изменяют свою величину и знак от опыта к опыту. Учет этих погрешностей требует специальной методики, которая рассмотрена ниже.
1.2. Приборная погрешность
Приборная погрешность определяется классом точности измерительного прибора и существенно зависит от его назначения. Для простых измерительных приборов (линейка, секундомер, микрометр, весы и т.д.) приборная погрешность ∆np принимается равной половине цены деления измерительного
прибора.
Цена деления измерительного прибора (С) – это значение измеряемой величины, которое приходится на одно деление шкалы прибора. Например, для миллиметровой линейки цена деления С = 1 мм, а приборная погрешность

6
∆np = 0,5 мм. Если цена деления штангенциркуля С = 0,1 мм, то приборная погрешность ∆np = 0,05 мм.
Для сложных измерительных приборов (например, амперметров и вольтметров) приборная погрешность определяется классом точности γ измерительного прибора, который указывается на его шкале и задается в паспорте. Класс точности γ измерительного прибора определяет в процентах относительную погрешность измерений прибора при предельном значении Апр измеряемой величины. Приборная погрешность в этом случае определяется по формуле:
∆Anp = γ Anp 100% . |
(1) |
Например, амперметр имеет класс точности γ = 2,5 %, а измерения проводятся на пределе Inp = 0,1 А. Тогда приборная погрешность измерений будет:
∆Inp = γ Inp 100% = 0,0025А. |
(2) |
1.3. Погрешности прямых измерений
Пусть некоторая величина А непосредственно измерена n раз. Средним значением величины А называется среднее арифметическое всех измерений
|
|
1 |
n |
|
Acp = A |
= |
∑Ai , |
(3) |
|
|
|
n i=1 |
|
|
где Ai - значение А в i -ом измерении (i = 1, 2,..., n). Среднее значение наиболее
близко соответствует истинному значению измеряемой величины. Абсолютной погрешностью i - го измерения называется величина, которая
определяется выражением
∆Ai = |
Ai − Acp |
. |
(4) |
Абсолютной погрешностью измерения называется величина |
|
||
|
n |
|
|
∆A = 1 ∑∆Ai , |
(5) |
||
|
n i=1 |
|
|
равная среднему арифметическому абсолютных погрешностей всех измерений.
Отношение абсолютной погрешности к среднему значению |
|
|||
δA = |
∆A |
|
(6) |
|
A |
||||
|
|
|||
называется относительной погрешностью измерения величины А. Относительная погрешность характеризует точность измерения. Чем
меньше относительная погрешность, тем точнее измерение.
Для оценки погрешности прямых измерений абсолютная погрешность измерений ∆A′ сравнивается с приборной погрешностью ∆Anp и выбирается
большая погрешность ∆A = max(∆A′,∆Anp ), которая и является погрешностью
прямых измерений. По формуле (6) определяется относительная погрешность измерений. Окончательный результат измерений записывается в виде
A = A ± ∆A. |
(7) |

7
Например, длина сторон a, b и с прямоугольного параллелепипеда, измеренная миллиметровой линейкой, равна: a = 80 мм, b = 50 мм и c = 20 мм. Абсолютная погрешность этих измерений ∆a = ∆b= ∆c = 0,5 мм. Относительная погрешность измерений будет
δa = ∆a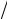 a = 0,006, δb = ∆b
a = 0,006, δb = ∆b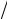 b= 0,01, δc = ∆c
b= 0,01, δc = ∆c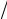 c = 0,025.
c = 0,025.
Отсюда видно, что наибольшую ошибку дает измерение стороны с параллелепипеда – около 2,5 %. Окончательный результат измерений записывается в виде
а = (80 ± 0,5) мм, b = (50 ± 0,5) мм, с = (20 ± 0,5) мм.
1.4. Погрешности косвенных измерений
На практике, как правило, искомую величину непосредственно измерить не удается или очень затруднительно. Очень часто искомая величина является функцией одной или нескольких непосредственно измеряемых величин. Такие измерения называют косвенными и погрешности этих измерений рассчитываются специальным образом.
Рассмотрим вначале на конкретных примерах погрешности измерений для функции одной переменной. Пусть некоторая величина f является функцией
измеряемой величины х, которая измерена с погрешностью ∆x . Тогда абсолютная погрешность этой величины определяется выражением
∆f = |
|
f (x + ∆x)− f (x) |
|
= df |
∆x . |
(8) |
|
|
|||||
|
|
|
|
dx |
|
|
|
|
|
|
|
Это выражение получено при разложении функции f (x + ∆x) в ряд Тейлора до
линейного члена ряда и последующего упрощения. Знак модуля поставлен потому, что нас интересует только абсолютное значение погрешности.
Относительная погрешность величины f определяется выражением
δf = |
|
∆f |
|
= |
|
1 df |
|
∆x . |
(9) |
|
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
f |
|
f dx |
|||||||
|
|
|
|
|
|
|
|
|||
Абсолютные и относительные погрешности косвенных измерений для некоторых элементарных функций приведены в табл. 1
Таблица 1. Абсолютные погрешности для функций одной переменной
№ |
функция |
абсолютная |
относительная |
||||||||||
погрешность |
погрешность |
||||||||||||
|
|
|
|
||||||||||
1 |
f (x)= xn |
∆f = nxn−1∆x |
δf = nδx |
||||||||||
2 |
f (x)= |
|
|
∆f = |
∆x |
δf = |
1 δx |
||||||
x |
|||||||||||||
|
|
|
|
|
|||||||||
|
2 x |
||||||||||||
|
|
|
|
|
|
2 |
|
||||||
3 |
f (x)= ln x |
∆ = ∆x |
δ = |
δx |
|
||||||||
|
|||||||||||||
|
|
|
f |
x |
f |
|
ln x |
||||||
|
|
|
|
|
|
|
|||||||
8
|
4 |
f (x)=sin x |
∆f = |
|
|
|
cos x |
|
∆x |
δf |
= |
|
ctg x |
|
δx |
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
5 |
f (x)= cos x |
∆f |
= |
|
|
sin x |
|
∆x |
|
δf |
= |
|
tg x |
|
δx |
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
6 |
f (x) |
= |
tg x |
∆ |
= |
|
|
∆x |
δf |
= |
|
|
|
|
|
|
δx |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
f |
|
|
|
|
|
|
cos2 x |
|
|
|
|
sin x cos x |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
7 |
f (x)= ctg x |
∆f |
= |
|
|
∆x |
|
δf |
= |
|
|
|
|
|
|
δx |
|
|
|||||||||||||||
|
|
|
sin2 x |
|
|
sin x cos x |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть некоторая величина f определяется через независимые величины x, y |
||||||||||||||||||||||||||||||||||
и z, измеряемые непосредственно, т.е. |
f |
= f (x, y, z). Так как величины x, y и z |
||||||||||||||||||||||||||||||||
измеряются с погрешностью, то и значение f будет найдено приближенно. Абсолютной предельной погрешностью величины f называется выражение
∆f = ∆fx + ∆f y + ∆fz , |
(10) |
где ∆fx , ∆f y и ∆fz погрешности измерений величины f, обусловленные каждой из измеряемых величин в отдельности, которые определяются по формулам (8)
∆fx = |
|
∂f |
|
∆x , |
∆f y = |
|
∂f |
|
∆y , |
∆fz = |
|
∂f |
|
∆z . |
(11) |
|
|
|
|
|
|
||||||||||
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В табл. 2 приведены абсолютные и относительные погрешности для некоторых простых функций двух переменных.
Таблица 2. Абсолютные погрешности для функций двух переменных
№ |
функция |
абсолютная |
относительная |
||||||
погрешность |
погрешность |
||||||||
|
|
|
|
||||||
1 |
f = x + y |
∆f = ∆x + ∆y |
δf = |
∆x + ∆y |
|||||
|
|
|
|
|
|
|
|
x + y |
|
2 |
f = x − y |
∆f = ∆x + ∆y |
δf = |
∆x + ∆y |
|||||
|
|
|
|
|
|
|
|
x − y |
|
3 |
f = x y |
∆f = y∆x + x∆y |
δf = δx + δy |
||||||
|
|
|
|
|
|
|
|
||
4 |
f = |
x |
|
∆f = |
y∆x + x∆y |
|
δf = δx + δy |
||
y |
y2 |
||||||||
|
|
|
|
|
|||||
1.5. Статистический метод учета погрешностей
В этом методе ошибки рассматриваются как случайные величины, которые обрабатываются методами теории вероятностей и подчиняются нормальному закону распределения Гаусса, который для случайной величины х имеет вид

9
|
|
1 |
|
|
e− |
(x |
− x )2 |
|
|
f (x)= |
|
|
|
|
2σ2 , |
(12) |
|||
|
|
|
|
|
|
||||
σ |
|
2π |
|
||||||
|
|
|
|
|
|
||||
где x - среднее значение величины х, |
σ - |
средняя квадратическая погреш- |
|||||||
ность, которая используется для оценки точности измерений.
Типичный вид кривой распределения Гаусса для примера, который рас-
смотрен ниже, приведен на рис. 1.1. |
f |
|
|
|
|
|
В статистической теории ошибок точ- |
|
|
|
|
|
|
ность измерений принято характеризовать |
0,8 |
|
|
|
|
|
одной из следующих величин: средней ошиб- |
|
|
|
|
|
|
кой (или абсолютная погрешностью) |
0,6 |
|
|
|
|
|
измерений ∆ и средней квадратической |
|
|
|
|
|
|
ошибкой измерений σ. Средняя квадратиче- |
0,4 |
a |
|
|
|
|
ская ошибка на рис. 1.1 соответствует |
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
абсциссам, которые проходят через точки пе- |
|
|
|
|
|
|
региба функции распределения. Она |
0 73 |
|
|
|
|
|
указывает на то, что истинное значение из- |
74 75 |
-σ 76 +σ |
77 |
a |
||
меренной величины с вероятностью Р = 0,683 |
|
|
|
Рис. 1 |
|
|
лежит в интервале 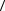 a
a − σ ≤ a ≤
− σ ≤ a ≤  a
a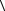 + σ. Такой
+ σ. Такой
интервал и вероятность называют доверительным интервалом и доверительной вероятностью.
Средняя ошибка (или абсолютная погрешность) для n измерений определяется по формуле
|
1 |
n |
|
||||
∆x = |
∑ |
|
xi − x |
|
. |
(13) |
|
|
|
||||||
|
n i=1 |
|
|
|
|
|
|
Средняя квадратическая ошибка для n измерений рассчитывается по формуле
σx = |
|
1 |
∑n (xi − x )2 |
. |
(14) |
|
|||||
|
|
n −1i=1 |
|
||
Средняя квадратическая ошибка среднего арифметического  x
x для n измерений рассчитывается по формуле
для n измерений рассчитывается по формуле
σ x = |
|
1 |
∑n (xi − x )2 |
= |
σ |
x |
|
. |
(15) |
|
|
|
|
||||||
|
|
||||||||
|
|
n(n −1)i=1 |
|
n |
|
||||
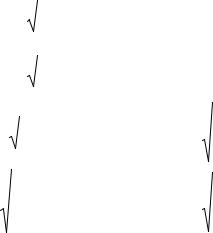
Если искомая величина f является функцией нескольких независимо измеряемых величин x, y, z и т.д. f = f (x, y, z,...), каждая из которых измерена со
средней квадратической погрешностью σx , σy , σz и т.д., то средняя квадратическая погрешность величины f определяется по формуле:
σ |
|
= |
∂f |
σ |
|
2 |
|
∂f |
σ |
2 |
∂f |
σ |
|
2 |
(16) |
|
f |
|
x |
|
+ |
|
|
+ |
z |
|
+... |
||||||
|
|
∂x |
|
|
|
∂y |
|
y |
∂z |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10
В табл. 3. приведены средние квадратические и относительные погрешности для некоторых простых функций одной и двух переменных.
Таблица 3. Средние квадратические и относительные погрешности для некоторых простых функций
№ |
функция |
средняя квадратическая |
|
относительная |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
погрешность |
|
|
|
|
|
погрешность |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σf |
|
|
|
|
|
|
|
|
1 |
f = x + y |
|
σf = σ2x +σ2y |
|
|
|
δf |
= |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x + y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σf |
|
|
|
|
|
|
|
|
2 |
f = x − y |
|
σf = σ2x +σ2y |
|
|
|
δf |
= |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x − y |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ2 |
|
σ2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
f = x y |
σf = y2σ2x + x2σ2y |
|
δf = |
|
|
|
x |
+ |
|
|
|
|
y |
|
||||||||||||||||||
|
|
|
|
y2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
σ2 |
||||||||||
4 |
f = |
|
|
|
σf |
= |
|
σx |
|
x |
|
2 |
|
δf = |
|
σx |
+ |
|
|
|
|
y |
|||||||||||
y |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
y |
2 + |
|
|
2 |
|
|
σy |
|
|
x |
2 |
|
y |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
σf = nx |
n−1 |
|
|
|
|
|
δf |
= |
|
nσx |
|
|
|
|
|
|
|
|||||||||||
5 |
f = x |
|
|
|
|
|
σx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.6. Метод границ
Для оценки погрешностей измерений можно воспользоваться методом границ, который достаточно прост в реализации. Метод основан на неравенствах и может применяться тогда, когда трудно получить простую формулу для расчета абсолютной или среднеквадратической погрешности. При методе границ определяют два значения физической величины: одно заведомо меньше истинного, называемое нижней границей величины (НГ), другое заведомо большее, называемое верхней границей (ВГ). Истинное значение искомой величины находится между верхней и нижней границами.
x = |
ÂÃ + ÍÃ |
, |
|
(17) |
|
|
|
||||
2 |
|
|
|
||
а величину погрешности определяют полуразностью этих границ |
|
||||
∆x = |
ÂÃ − ÍÃ |
. |
(18) |
||
|
|||||
2 |
|
|
|
||
Результат измерений записывают в виде |
|
||||
x = x ± ∆x . |
(19) |
||||
В этом разделе мы рассмотрели три метода оценки погрешностей измерений: метод максимальной абсолютной погрешности, метод средней квадратической погрешности и метод границ. Все они могут быть использованы при обработке результатов измерений. Наиболее строгим, но и трудоемким

11
является метод средней квадратической погрешности, который широко используется в научно-исследовательской работе. Очень неплохие результаты дает метод максимальной абсолютной погрешности. Для предварительной оценки результатов можно использовать метод границ.
В теории погрешностей доказывается, что оценка погрешностей разными методами дает результат, который различается в пределах погрешностей. Поэтому не имеет особого значения метод, которым рассчитываются погрешности. Однако, среднеквадратическая погрешность дает больше информации о погрешности измерений, т.к. кроме погрешности дает и вероятность этой погрешности, которая указывается в доверительном интервале. Эта дополнительная информация требует более сложных и трудоемких расчетов.
1.7. Обработка и запись результатов измерений
Порядок обработки результатов прямых измерений
1.Определяем среднее значение 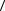 A
A измеряемой величины по формуле (3).
измеряемой величины по формуле (3).
2.По формулам (4) и (5) находим абсолютную погрешность каждого измерения и среднюю абсолютную погрешность измерений величины А. Сравниваем эту погрешность с приборной и выбираем максимальную погрешность ∆Amax .
3.По формуле (6) вычисляем относительную погрешность измерений.
4.Записываем окончательный результат измерений с учетом погрешности:
A = A ± ∆A. |
(20) |
Например, запишем измерение длины нити математического маятника. Измерения проводили линейкой с ценой деления 1 мм. Получили результаты:
l1 =30,6 см, |
l2 =30,4 см, l3 =30,5 см; вычисляем среднее значение l =30,5 см, |
абсолютную |
и относительную погрешности измерения ∆A = 0,1 см, |
δA = 0,0032. |
Сравниваем абсолютную погрешность измерения и приборную |
погрешность линейки ∆Aïð = 0,05 см, т. к. приборная погрешность меньше абсолютной, то окончательный результат записываем в виде l = (30,5 ± 0,1) см.
Порядок обработки результатов косвенных измерений
1.По изложенной выше методике находим средние значения и абсолютные
погрешности x, y, z прямых измерений величин x, y, z, которые содержаться в формуле для вычисления величины f (x, y, z).
2. По средним значениям прямых измерений величин x, y, z рассчитываем среднее значение величины f косвенных измерений
f = f ( x , y , z ). |
(21) |
3.Находим абсолютную предельную погрешность величины f по формуле
∆f = |
|
∂f |
|
∆x + |
|
∂f |
|
∆y + |
|
∂f |
|
∆z . |
(22) |
|
|
|
|
|
|
||||||||
|
|
∂x |
|
|
|
∂y |
|
|
|
∂z |
|
|
|
4. Относительную погрешность величины f |
|
определяем по формуле |
|
||||||||||
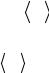
12 |
|
||
δf = |
∆f |
(23) |
|
f |
|||
|
|
||
5.Результат опыта записываем в виде
f = f ± ∆f . |
(24) |
При обработке результатов измерений нужно придерживаться следующих правил:
1.При записи погрешности следует округлить ее величину до двух значащих цифр, если первая из них меньше 3 и до одной значащей цифры в остальных случаях (значащими цифрами называют цифры в числе, начиная с первой отличной от нуля).
2.В записи результата измерений следует указывать все известные цифры (даже если они нули) вплоть до последнего разряда, имеющегося в значении погрешности этого результата. Например, полученное нами значение плотно-
сти тела (п. |
2.2) |
ρ = 2,7389 |
г/см3, абсолютная погрешность измерения |
||||
∆ρ = 0,2543 |
г/см3, |
тогда |
результат |
следует |
записать |
в |
виде |
ρ= (2,74 ± 0,25) г/см3.
3.В промежуточных расчетах можно сохранять лишние цифры, которые
взаписи окончательного результата будут отброшены при округлении.
4.Обязательно нужно в выводе к лабораторной работе записать полученный результат с учетом погрешности.
Приведем пример записи результатов измерений по расчету ускорения
свободного падения (п. 2.3). На основании произведенных измерений определено среднее значение измеряемой величины g =982,5 см/с2 и абсолютная
погрешность измерений ∆g = 2 см/с2. Очевидно, что вычислять результат с
точностью до сотых долей бесполезно, так как ошибка содержится уже в целых единицах ( ∆g = 2 см/с2) и все дальнейшие знаки являются излишними. В дан-
ном случае среднее значение измеряемой величины следует записать так: g =982 см/с2. Результат измерений согласно формуле (24) запишем в виде:
g = (982 ± 2) см/с2.
Литература
1. Физический практикум. Механика и молекулярная физика / Под ред В. И. Ивероновой. - М.: Наука, 1967. - С. 11-39.
