Работа и энергия

Работа. Энергия. Кинетическая и потенциальная энергии. Полная механическая энергия. Закон сохранения энергии в механике. Работа переменных сил.

Работа переменной силы

П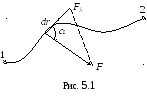усть частица под действием силыосуществляет перемещение по некоторой траекторией 1 -2 (рис. 5.1). Действие силына перемещениихарактеризуетсявеличиной, которая равняется скалярному произведению, которое называют элементарной работой силы на перемещении . По определению элементарной работы, имеем:

(5.1)

где  - угол между векторами силы и перемещения. Если угол острый - работа позитивная и кинетическая энергия системы растет. Если угол  тупой - работа отрицательная и кинетическая энергия системы уменьшается. Если  = /2 работа внешних сил равняется нулю.

Действительно, общая работа научастке r₁ - r₂ запишется в виде:

. (5.3)

Если на частицу в процессе движения действует несколько сил, результирующая которых равняется , тогда нетрудно показать, что работа результирующей силына некотором перемещении равняется алгебраической сумме работ, которую осуществила каждая из сил отдельно на том же перемещении. Действительно

,

Работа измеряется в единицах – Джоуль (Дж). Это производная единица. Она связана с основными единицами системы СИ соотношением:

1 Дж =1 Н 1 м.

3.2. Мощность

Работа, совершаемая в единицу времени, называют мощностью

. (5.4)

Мощность измеряется в единицах, которые зовутся Ватт (Вт):

1 Вт = 1 Дж /1 с.

С (5.4) выплывает очень важное в практическом плане соотношение:

(5.5)

или, мощность определяется скалярным произведением силы на скорость.

Кинетическая энергия

Учитывая второй закон Ньютона, определение (5.1) можно записать в виде:

где - скорость тела, - приращение импульса тела при перемещении. В нерелятивистском случае. Можно показать, что при изменении величины скорости отV до V+dV совершается работа:

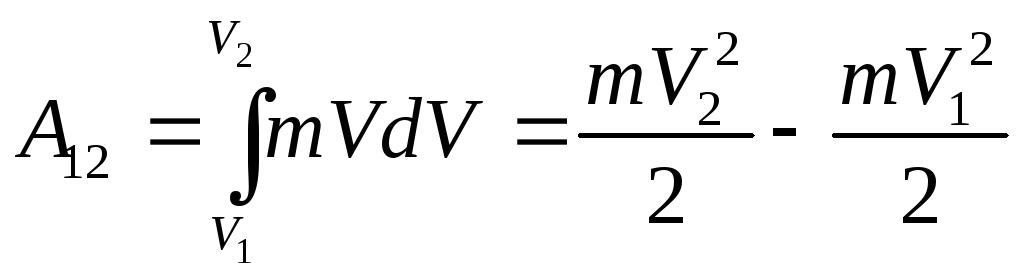(5.6)

Величину называют кинетической энергией тела -.

Тогда (5.6) можно переписать в виде:

Т.е., работа силы, действующей на тело, идет на приращение его кинетической энергии. Это утверждение называют теоремой об изменении кинетической энергии.

Кинетической энергией системы называется сумма кинетических энергий частиц, составляющих эту систему. Тогда приращение кинетической энергии системы равно суммарной работе всех сил, действующих на систему материальных точек.

Если во всех точках поля силы, действующие на частицу, одинаковы по величине и направлению, поле называется однородным. Поле, изменяющееся со временем, называется нестационарным. Поле, остающееся постоянным во времени, называют стационарным. Для стационарного поля может оказаться, что работа, совершаемая над частицей силами поля, зависит лишь от начального и конечного положений частицы, и не зависит от пути, по которому двигалась частица. Такие поля и силы называют потенциальными или консервативными.

Силы, работа которых не зависит от пути перехода, называют консервативными, а такие силовые поля – потенциальными или консервативными. Работа потенциальной силы вдоль замкнутой траектории равна нулю. Математически такое свойство силового поля записывается в виде:

(5.6)

то есть, работа сил притяжения по замкнутому кругу всегда равняется нулю. Свойством (5.6) владеют не все силы. Например, сила трения таким свойством не владеет: работа этой силы зависит не только от положения начальной и конечной точки, но и от формы пути между ними. Такие силы называют диссипативными.

Потенциальная энергия тела в однородном поле тяжести. Пусть тело массы m под действием силы тяжести перемещается из точки 1 в точку 2 (см.рис). Сила тяжести совершает работу:

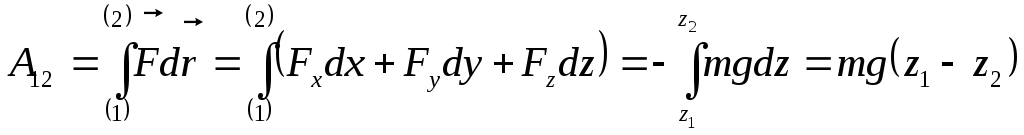. (5.7)

Работа силы тяжести не зависит от формы траектории, а зависит лишь от значений начальной z₁ и конечной z₂ координаты. Если в качестве нулевого положения тела принять его положение в точке с координатой z₂ и обозначить высоту точки 1 над нулевым уровнем через h, то потенциальная энергия тела массы m в точке 1

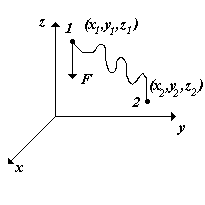
Потенциальная энергия растянутой пружины. Если пружина растянута

вдоль оси Ох на величину х, то величина силы упругости . Примем в качестве нулевого положения, положение, когда пружина не растянута (х=0). Тогда потенциальная энергия растянутой пружины

Работа сил потенциального поля равна убыли потенциальной энергии