1.2. Ряды Фурье

Базисные функции в рядах Фурье являются гармоническими сигналами и, гдеn и k целочисленные индексы а ₁ – круговая частота первой гармоники ₁=2Т.

Докажем ортогональность этих функций основываясь на (4).

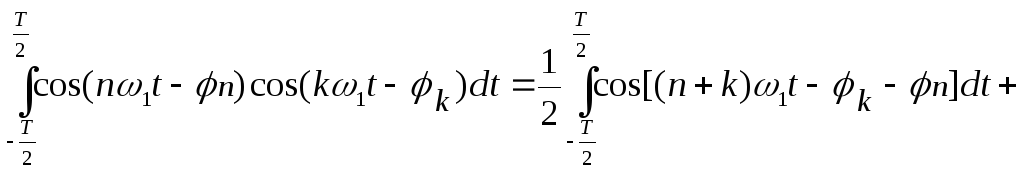
. (8)

Рассмотрим первый случай, когда n  k. Тогда (n + k) и (n – k) целые числа. Если же вычисляется интеграл от них, то получается следующее. Так как подынтегральная функция знакопеременная, а интегрирование идет в пределах кратных Т, результат будет равен нулю. На рис. 6 показаны подынтегральные функции при n + k = 1 и n + k = 2.

t

t

T t

Рис.6 Гармонические базисные функции

Таким образом, если n  k, то оба этих интегралов всегда дадут нам нулевое значение, что и требуется при ортогональности.

Теперь предположим, что n=k. Первый интеграл в (8) будет равен нулю по причине изложенной выше. Второй интеграл в (8) имеет следующее решение (учтите, что _n=_k ):

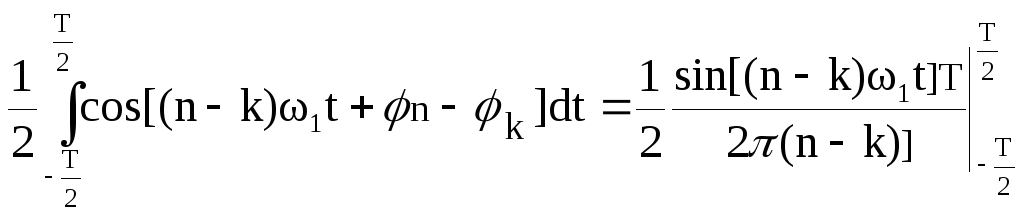. (9)

При подстановке пределов с учетом, что , получается выражение известного пределаи решение будетT/2. Таким образом свойство

ортогональности функций доказано. Следовательно, будет и ортогональным ряд на их основе. Имеется несколько форм ряда Фурье.

Первая форма ряда имеет следующий вид:

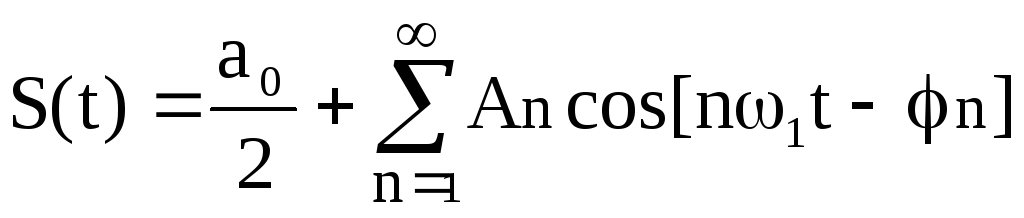. (10)

Каждый член ряда называется гармоникой. У каждой гармоники есть своя амплитуда и фаза.

Здесь An – коэффициенты ряда, которые получили названия амплитуд гармоник, они всегда положительные; n – начальные фазы гармоник.₁– частота первой гармоники, где T – период сигнала . Текущая частота определяется как=₁n. Слагаемое в правой части получило название постоянной составляющей сигнала.

Вторая форма ряда записывается как

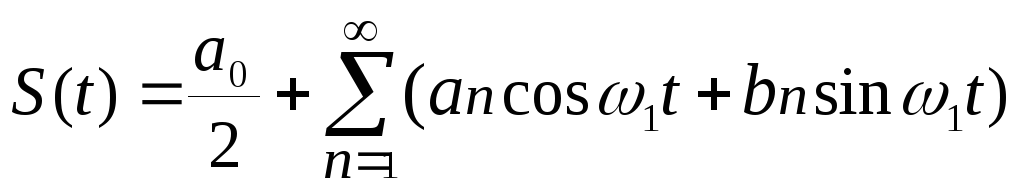. (11)

- коэффициенты ряда, которые могут принимать любые значения в том числе и по знаку. a_ncos1t и b_nsin1t косинусные и составляющие ряда. Амплитуда , фаза . Коэффициенты ряда определяются по общему для ортогональных рядов принципу:

; (12)

- коэффициент при косинусной составляющей

; (13)

- коэффициент при синусной составляющей

. (14)

Существует также и комплексная форма ряда Фурье, в которых суммируются гармоники с комплексными амплитудами An`:

. (15)

Здесь - комплексная гармоническая базисная функция

Появление отрицательных частот в (15) при отрицательных n есть следствие применения комплексного исчисления. Легко доказать, что отрицательных частот нет. Разберём 2 члена ряда n = 1 и n = -1. По свойствам комплексного переменного модуль комплексной амплитуды чётная функция индекса (А_n = A_-n), фаза комплексной амплитуды – нечётная функция индекса (-_n = _-n). Тогда сложив два члена ряда получим

. (16)

В результате получилась обычная вещественная гармоника, что и требовалось доказать.