ТПС / Лекции / Лекция 12

Лекция 12

Методы обработки сигналов в приемнике

Ранее нами было установлено, что основным звеном обработки в оптимальном приемнике является коррелятор. Результат на его выходе можно записать так:

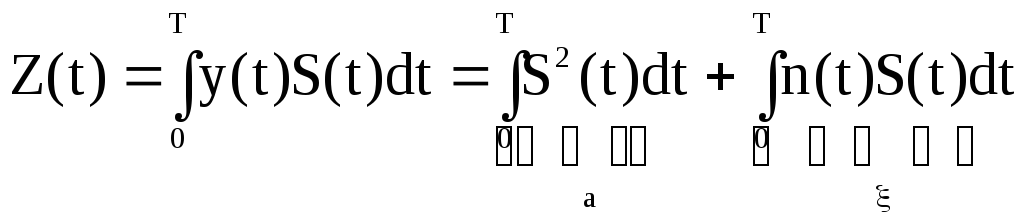. (1)

Первый интеграл, детерминированное слагаемое - энергия, зависящее только от сигнала.

Второй интеграл отражает взаимную корреляцию сигнала и помехи, характеризует статистическую связь.

По своей природе помеха никак не связана с сигналом, поэтому корреляции между ними нет. Следовательно, второй интеграл при определенных условиях стремится к нулю, в то время как первый к величине энергии полезного сигнала. Таким образом коррелятор повышает отношение сигнал/помеха. Представляет интерес рассмотреть другие устройства с таким же эффектом. Они могут применяться в качестве устройства оптимальной обработки.

При линейном способе обработки представим результат в следующем виде:

, (2)

φ(t) – временной функционал определяемый методом обработки . можно ввести следующую градацию методов.

1. Корреляционный приемник , .

2. Синхронный детектор, .

3. Интегральный приемник, .

4. Автокорреляционная обработка, .

5. Метод оптимальной фильтрации, – характеристика фильтра согласованного с сигналом.

Выше мы уже провели анализ работы синхронного детектора и теперь рассмотрим другие методы.

Интегральный метод приема

Метод может быть применен при непрерывной и дискретной обработке для некоторых видов сигналов (см. рис. 1)

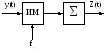
а) б)

Рис. 1. Интегральный метод приема,

а) непрерывная обработка, б) дискретная обработка.

Сигнал на выходе при дискретной обработки будет представлен так:

, (3)

где S_h и n_h – отсчеты сигнала и помехи.

Найдем отношение мощностей сигнала и помехи на выходе. Мощности наиболее объективно отражают их характеристики так как дают представление о величине сигнала и время его существования. Тогда мгновенная мощность сигнала в момент его окончания будет

. (4)

Если , то есть сигнал постоянен во времени, то .

Найдем мощность случайной помехи, его дисперсию. Для этого воспользуемся формулами статистики известными из теории сигналов.

Если помеха имеет на входе и выходе нулевое математическое ожидание, то 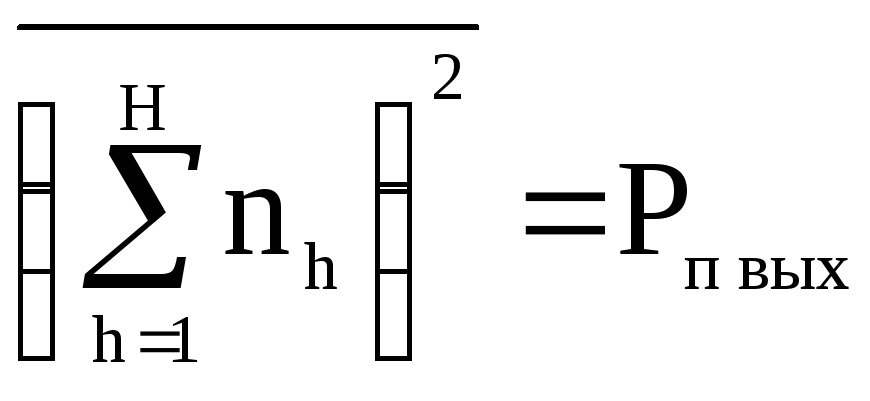(черта сверху означает усреднение). Квадрат суммы можно представить следующим образом:

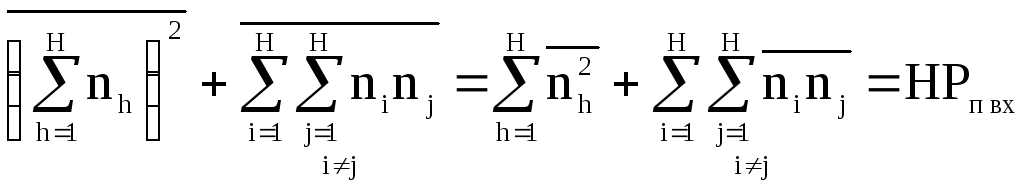, (5)

где .

Двойная сумма по смыслу взаимная корреляция между двумя отсчетами сигнала. Если интервал корреляции помехи  меньше временного шага дискретизации t статистическая связь отсутствует и данная величина равна нулю. Таким образом, отношение мощности сигнала к мощности помехи будет

. (6)

Чем больше Н, тем больше выходное соотношение сигнал/помеха.

Таким образом, интегральный метод увеличивает соотношение сигнал/помеха. На рис. 2 показано как интегрируется сигнал, постепенно наращивая значения . Помеха же имея знакопеременный характер на выходе интегратора приближается к нулю (при условии ).

Рис. 2. Интегрирование сигнала и помехи.

Метод оптимальной фильтрации

Метод реализован на полосовом фильтре (рис. 2) с характеристикой передачи согласованной с характеристикой сигнала (частотной и временной). При таком согласовании в момент времени t₀>=T получается максимальное отношение пиковой мощности сигнала к помехе.

Рис. 2. Оптимальный фильтр

Как и прежде будем считать что помеха представляет собой белый шум, то есть ее спектральная плотность постоянна, . Поставим цель определить характеристики фильтра, и будем решать задачу в частотной области. Характеристика его передачи . Напомним, что спектральная плотность помехи G() характеризует распределение по спектру ее мощности и имеет размерность Вт/Гц. Коэффициент K() дает представление о том как напряжение (Вольты) проходят на выход фильтра. Поэтому K²() характеризует передачу мощности и спектральная плотность мощности помехи на выходе фильтра будет

. (7)

Функция автокорреляции помехи может быть найдена преобразованием Виннера-Хинчина по спектру (7):

. (8)

Одно из свойств найденной функции заключается в том, что при =0 она принимает максимальное значение равное мощности помехи, . Таким образом, находим выражение для мощности помехи:

,

. (9)

Далее найдем мгновенную мощность сигнала в определенный момент времени t₀. Задачу будем решать также спектральным методом. На входе фильтра имеем временной сигнал, которому соответствует спектральная плотность определяемая посредством преобразования Фурье, . Пользуясь характеристикой передачи фильтра, найдем спектр сигнала на выходе и далее временную функцию:

. (10)

Мгновенное значение сигнала при t=t₀ будет:

. (11)

Квадрат модуля S(t₀) – мгновенная мощность сигнала. Таким образом, отношение мощностей сигнала и помехи будет равно:

. (12)

Воспользуемся приближенной оценкой интеграла в числителе (12), которая известна как неравенство Буняковского-Шварца. В общем случае для интеграла от произведения двух любых функций оно позволяет установить неравенство :

. (13)

Тогда отношение (12) подчиняется следующему неравенству:

(14)

Правая часть неравенства (14) – максимальное отношение сигнал/помеха q_мах:

. (15)

Остается выяснить, при какой характеристики передачи в частотной области K(j) неравенство (14) обращается в равенство. Примем, что фазовая характеристика фильтра равна сумме с обратным знаком фазовой характеристики сигнала _s() и величине t₀, . Модуль же характеристики передачи равен , то есть с точностью до постоянного множителя «с» повторяет модуль спектральной плотности сигнала. На рис. 3, 4 показаны характеристики сигнала и согласованного с ним фильтра.

Рис. 3. Модули спектральной плотности и

коэффициента передачи

Рис.4. Фазовые характеристики сигнала и фильтра.

Далее разберем ,что дает фильтр с такими характеристиками. Для этого обратимся к левой части неравенства (14) и вместо K(j) подставим в него принятую нами характеристику фильтра cS()exp(-_s()-t₀):

. (16)

Учитывая, что произведение экспонент с показателями равными по величине но разными по знаку, равно 1, получим в правой части (16) q_мах , что и требовалось доказать. Таким образом, действительно, фильтр имеющий характеристики передачи

,

, (17)

максимизирует отношение сигнал/помеха в момент времени t₀. В момент t₀ произойдет согласованное сложение всех составляющих сигнала, мы получим пик сигнала.

Импульсная характеристика оптимального фильтра.

Синтезировать оптимальный фильтр можно либо в частотной области, либо во временной. В последнем случае требуется знать его импульсную характеристику, то есть реакцию на короткий импульс – дельта функцию (рис. 5).

Рис.5. Импульсная реакция фильтра.

Спектральная плотность дельта-функции не зависит от частоты, , поэтому на выходе оптимального фильтра . По спектру найдем импульсную реакцию (обратное преобразование Фурье):

. (18)

Введем новую переменную ₁=- и так как модуль спектральной плотности четная функция частоты а фаза – нечетная выражение (18) будет записано так:

. (19)

Согласно свойствам преобразования Фурье, права часть выражения (19) представляет зеркальное отображение сигнала S(t), которое записывается так: сS(t₀-t), то есть . Мы установили интересное свойство импульсной характеристики оптимального фильтра, которое позволит осуществить его синтез. На рис. 6 показан сигнал S(t) и его зеркальное отображение сS(t₀-t). Для реализации фильтра необходимо выполнить два условия. Во- первых сигнал должен быть конечен во времени, во-вторых t₀≥T. Несоблюдение этого приводит к тому, что импульсная реакция на короткий импульс должна начаться до его прихода на вход фильтра, что в принципе невозможно.

Рис. 6. Сигнал и импульсная реакция фильтра.

Рассмотрим оптимальный фильтр для простейшего сигнала, прямоугольного длительностью Т. Потребуем максимума отношения сигнал/помеха в момент времени t₀=T. Тогда зеркальное отображения сигнала будет сам сигнал. Таким образом мы определили требования к фильтру; при подаче на вход короткого импульса на выходе должен быть прямоугольный сигнал. Его структура показана на рис.7 и состоит из интегратора, линии задержки и вычитателя, а на рис. 8 эпюры поясняющие его работу.

Рис. 7. Структура оптимального фильтра.

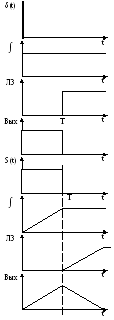
Рис.8. Работа оптимального фильтра.

В момент времени Т произойдет суммирование знакопеременного значения помехи, что в итоге даст близкое к нулю значение. В этот же момент все спектральные составляющие сигнала будут иметь одинаковую фазу и сложатся согласно, что даст пик сигнала.

По такому же принципу можно составить оптимальный фильтр для радиоимпульса (модулированный сигнал); на рис. 9 показана его структура.

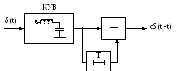
Рис. 9. Оптимальный фильтр для радиоимпульса,

КУВ – контур ударного возбуждения.

Реализация оптимального фильтра для любого сигнала выполняется с помощью трансферсального фильтра. Это конструкция состоящая из линии задержки с отводами (ЛЗ) масштабирующих звеньев передачи (Ki), сумматора и сглаживающего фильтра ФНЧ (Рис. 10).

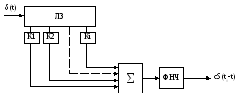
Рис. 10. Трансферсальный фильтр

Подбирая коэффициенты масштабирующих звеньев можно получить на выходе сумматора выборку зеркального отражения (Рис. 11). С помощью ФНЧ она восстанавливается.

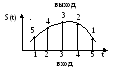
Рис. 11. Зеркальное отображение выборки.

В заключении отметим следующее. Обычный полосовой фильтр, рассчитанный на пропускания спектра частот сигнала дает на выходе проигрыш в отношении сигнал-помеха на 20…30%. Таким образом выигрыш, получаемый с помощью оптимального фильтра, в некоторых случаях не велик и он может быть заменен обычным полосовым фильтром.

Автокорреляционный метод приема

Здесь м в качестве опорного сигнала используется принимаемый задержанный на определенное время. Таким образом производится вычисление функции автокорреляции входного сигнала (Рис. 12).

Рис. 12. Автокорреляционный прием.

Запишем сигнал на выходе интегратора:

, (20)

где , .

Запишем интеграл (20)

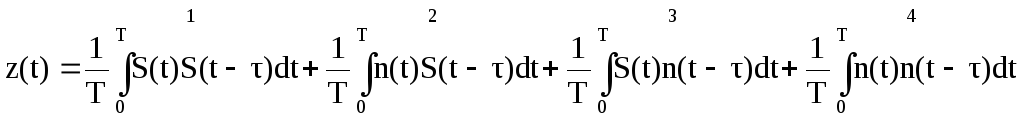, (21)

и разберем смысл каждого.

Допустим, что сигнал гармоническая функция; тогда первый интеграл имеет значение функции автокорреляции периодического сигнала. Из теории случайных сигналов известно, что АКФ такого регулярного сигнала также гармоническая функция. Ее значение зависит от величины задержки . Выбирая задержку , можно получить максимальное значение интеграла (рис. 13).

Второй и третий интегралы дают представление о статистической связи между сигналом и помехой. Статистической связи между ними нет, значит эти интегралы равны нулю.

Четвертый интеграл – автокорреляционная функция помехи. Как следует из ее свойств, она уменьшается с ростом  и при достаточно больших временах приближается к нулю (рис. 14).

Рис. 13. АКФ сигнала. Рис. 14. АКФ помехи

Выбирая τ>Δτ, то есть время задержки больше интервала корреляции помехи, можно получить положительный эффект в отношении сигнал-помеха . Поскольку длительности сигналов в связи конечны, необходимо также выполнить неравенство Т> τ. Метод автокорреляции может быть применен при приеме модулированных сигналов АМ, ЧМ, ОФМ.