1.3.Теоремы Шеннона для канала без помех.

На основании производительности источника и пропускной способности канала основана первая теорема К. Шеннона для канала без помех.

Если производительность источника меньше пропускной способности канала , , где - сколь угодно малая величина, то по такому каналу можно передать все сообщения источника.

Руководствуясь желанием передать, как можно большее количество информации, мы можем повышать производительность источника до предела, которым является пропускная способность канала. На первом этапе можно просто заставить источник "говорить", создавать информацию, быстрее; канал обладает резервом по времени и успевает ее передать. Это положение иллюстрируется на рис.6.

Р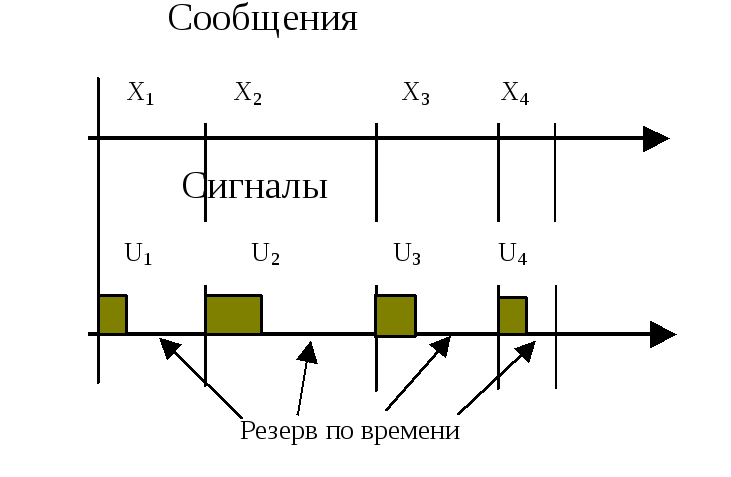 ис. 6

При дальнейшем уменьшении длительностей сообщений сигналы начнут "сливаться" и возникает задача сокращения времени каждого из них. А это уже задача кодирования , то есть закона преобразования сообщения в сигнал.

Существует следующее понятие: "статистическое или оптимальное кодирование". Оно позволяет приблизить скорость передачи к пропускной способности канала и, следовательно, обеспечить наилучшее использование канала без помех. Рассмотрим основные принципы такого кодирования на примере источника независимых сообщений, который необходимо согласовать с двоичным каналом. Вспомним принцип кодирования: это запись сообщений в виде двоичных чисел. Каждые 0 и 1 такого числа – электрические сигналы. Предположим, что длительность такого элементарного сигнала . Для каждого сообщения представляется сигналом ,которое представляет собой двоичное число имеющее разрядов. Таким образом, длительность сигнала будет равна . Сколько сообщений, столько сигналов и столько же длительностей.

Усреднив длительности, получим среднюю продолжительность сигнала:

.

Далее определим скорость передачи :

.

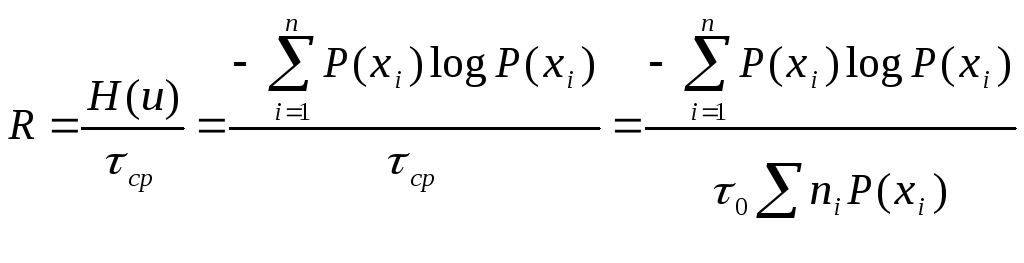Пропускная способность двоичного канала равна:

.

По последним двум формулам найдем условие, при котором скорость передачи приближается к пропускной способности канала . Очевидно, для этого необходимо потребовать равенства

.

Как видно из последнего, число разрядов кода определяется вероятностью сообщения. Вывод таков. Для того, чтобы приблизить скорость передачи к пропускной способности канала следует сообщения источника, имеющие большие априорные вероятности кодировать короткими комбинациями, а сообщения с малыми априорными вероятностями –длинными. Это правило построения оптимального статистического кода. Остановимся на некоторых его особенностях.

Во-первых, оптимальный код неравномерный; его комбинации имеют различное количество двоичных разрядов. Отделить такие комбинации друг от друга возможно только при наличии специальных (разделительных) символов, которыми дополняется каждая кодовая комбинация.

Во-вторых, такой код, хотя и повышает скорость передачи по каналу, совершенно не защищен от воздействия помех. Это не помехоустойчивый код.

Для облегчения формирования кодовых комбинаций существуют алгоритмы Шеннона-Фано и Хафмена. Принципы их работы простые и похожи. Рассмотрим алгоритм статистического кодирования Хафмена. Обычно для этого заполняется таблица по следующему принципу.

1.В первых двух столбцах располагают сообщения по убыванию их априорных вероятностей.

2.В первом вспомогательном столбце также записываются сообщения по мере убывания вероятностей, но самая последняя записывается в виде суммы двух последних предыдущего столбца.

3.Последующие вспомогательные столбцы записываются по такому же принципу. Последний вспомогательный столбец представлен "1".

4. По данным таблице строится граф с вершиной "1". Ребра графа отражают вероятности, причем ребру с большей вероятностью присваивается значение "1", а с меньшей – "0".

5.Код сообщения получим проходя по ребрам от сообщения к вершине и фиксируя присвоенные значения.

Рассмотрим все это на примере источника информации состоящего из 4-х сообщении. Начнем заполнять таблицу.

Сообщение		Вспомогательные столбцы			Код
		1	2	3
	0.6	0.6	0.6	1	1
	0.15	0.25	0.4		00
Сумма	0.13	0.15			110
Сумма	0.12				010

По данным таблицы построим граф.

1

0.6/1

0.4/0

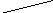
0.15/0

0.25/1

0.12/0

0.13/1

Присвоенные, таким образом, значения ребрам 0 или 1 и есть кодовые комбинации. Остается только выписать их значение идя в направлении от сообщения к вершине графа. Результирующие коды приведены в таблице.

1.4. Пропускная способность канала с помехами.

Теорема Шеннона.

Воспользуемся моделью канала с помехами , которая изображена на рис.2. Конечно, при воздействии помех становятся возможны ошибочные переходы на графе и -тому передаваемому сообщению не обязательно соответствует -тый принятый. В приеме возникает неопределенность.

Определим энтропию сигнала в таком канале.

Обозначим P(х_i) – априорную вероятность передаваемого сигнала. Допустим, произошла передача и принят сигнал , который позволяет судить о переданом. Введем апостериорную вероятность P(x_i/y_j). По сути мы провели опыт (передачу сигнала) и две вероятности: доопытную (априорную ) P(х_i) и послеопытную (апостериорную) P(x_i/y_j). Для понимания их смысла полезно обратится к модулю 2. Далее воспользуемся определением меры количества информации, как уменьшением меры неопределенности и определим ее при данных условиях:

.

Е сли далее это количество информации прошедшее по каналу усреднить по всем возможным вариантам приема и передачи, получим энтропию канала с помехами. Напомним, что усреднение есть суммирование с весовыми коэффициентами. Тогда

П роведем анализ этого выражения, для чего воспользуемся теоремами статистики:

п осле чего получаем

Рассмотрим смысл двойных сумм. Внутренняя сумма по i в первой - по смыслу частная энтропия при фиксированном , . Внешняя же сумма по j приводит нас к условной энтропии со знаком минус. Во второй двойной сумме действие над условной вероятностью дает 1, так как это составляет полную группу событий и она равна . Таким образом, получаем следующую формулу для энтропии канала с помехами:

, или

.

В результате анализа нам удалось представить энтропию канала с помехами в виде алгебраической суммы двух одномерных энтропий первые из них и , характеризующих среднее количество информации в передаваемых и принимаемых сигналах (энтропии передатчика и приемника). Условные же энтропиии имеют очень интересный смысл. Запишем отдельно одну из них, например и поясним ее смысл

Допустим, помех нет. Граф канала будет представлен прямыми горизонтальными ребрами; ошибочных переходов не будет (рис.2). Условные вероятности будут равны либо 1, если , либо 0,если . Таким образом, в этом выражении каждый член суммы будет равен нулю; .

Допустим другой крайний случай, помехи очень сильны. Ошибочные переходы на графе рис.2 столь же вероятны, как и правильные. Согласно законам статистики условные вероятности становятся безусловными, так как теперь не определяет ; . Не трудно видеть, что условная энтропия , а энтропия канала с помехами . Таким образом, передачи информации по каналу не происходит.

Подобный анализ можно провести и для другой формулы ( ). В обоих случаях условные энтропии характеризуют степень воздействия помех на канал и дают численное представление о потерях информации (бит/знак). Введены следующие термины: - энтропия ненадежности, - энтропия шума.

Предположим, что - среднее время передачи сообщения по каналу, тогда скорость передачи информации по каналу будет равна

, (бит/знак*с).

Величина -пропускная способность канала.

Пропускная способность канала зависит от следующих факторов:

1. от статических свойств источника,

2. от интенсивности помех,

3. от полосы пропускания , которая определяет среднее время передачи сигнала.

Итак, мы ввели информационные характеристики канала с помехами.

В качестве примера найдем энтропию и пропускную способность двоичного канала. Его граф показан на рис.5.

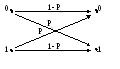
Рис.5

Предполагаем , что длительность нулевых и единичных сигналов равны .

Тогда

.

Согласно свойству энтропии и

Найдем информационные потери, ненадежность:

.

Выше обозначено: - ошибочный переход, - правильный переход. После чего получим

Если p₀=0, то и при p₀=0.5 , то есть передача невозможна.

Теорема Шеннона для канала с помехами. Пусть - производительность источника, тогда, если производительность источника меньше пропускной способности канала (), то можно передовать сообщения со сколь угодно высокой достоверностью.

Шеннон впервые указал на то, что можно сделать. Ему принадлежит идея помехоустойчивого кода. Ранее, до Шеннона, повышение помехоустойчивости достигалось многократной передачи одной и той же информации и вынесением решения по большинству голосов. Это было крайне не рационально для канала, так как для передачи требовалось большее время. Теорема Шеннона, хотя и не конструктивна, утверждает что достоверность можно повысить другим методом – путем построения помехоустойчивого кода. В дальнейшем это положение было подробно разработано с применением математического аппарата комбинаторики и в теории связи появилось научное направление "помехоустойчивое кодирование". В данном разделе мы не будем его подробно рассматривать, а ограничимся изучение помехоустойчивого кода с проверкой на четность. Формирование этого кода идет по схеме показанной на рис.2.

Рис. 2

Кодер канала формирует помехоустойчивый код по первичному коду сообщения. Рассмотрим как это делается. Допустим первичный код представлен r разрядами (в данном на рис.3 примере 6 разрядов).

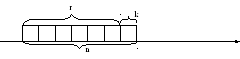
Рис.3

В комбинацию кода вводится еще один разряд k, который называется контрольным. Его значение определяется по очень простому правилу: количество единиц во всем кодовом слове должно быть четным. Например, r разрядов 011101, контрольный разряд k равен 0; r – 001110, k – 1. Это правило формирования кода известно в приемнике и его задача проверить выполнение условия. Если количество единиц четное, ошибок нет и информация поступает получателю. Если же нет, приемник вырабатывает сигнал ошибки, по которому запрашивается повторная передача. Такое правило позволяет обнаружить однократные ошибки. Существуют более сложные помехоустойчивые коды не только обнаруживающие, но и исправляющие ошибки.

Информационные характеристики непрерывных

источников и каналов связи.

.