Контактные сети и ЛЭП

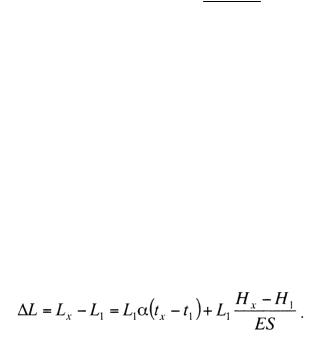
Lx = L1 [1 + α (t x − t1 )](1 + H x − H1 ).

ES

Раскрыв квадратные скобки, получим

Пренебрегая последним членом как малой величиной второго порядка (произ-

ведение двух малых величин) и вычитая из обеих частей уравнения начальную дли-

ну L1, получим приращение длины провода

Учитывая, что длина провода L для обычных соотношений незначительно от-

личается от длины пролета l, примем для определения приращения L1= l . Тогда

(3.38)

С другой стороны, приращение длины может быть представлено как разность между начальной и конечной длиной (3.22)

(3.39)

Приравняв уравнения (3.39) и (3.38) и разделив обе части на l, получим

(3.40)

Умножив обе части уравнения на ЕS, будем иметь

(3.41)

Уравнение (3.41) симметрично. Это ясно видно, если в крайнем члене правой части открыть скобки и перенести αЕStx, влево.

В таком виде этим уравнением можно пользоваться, полагая величины для ре-

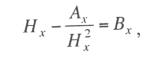
жима с индексом «1» известными и определяя величины для режима с индексом

«х», или наоборот. Однако наибольшее распространение уравнение (3.41) получило в том виде, как оно написано. При проведении расчета для ряда режимов удобно за-

менять индекс «х» последовательно индексами «2», «3», «4» и т. д. Уравнение (3.41)

по подстановке известных величин получает вид:

(3.42)

где

Стрела провеса провода f определяется по формуле (3.19)

Это же уравнение, выраженное через удельные значения нагрузок и натяжений,

имеет вид

(3.43)

Стрела провеса может быть определена по формуле (3.41). В том случае, когда нагрузка q представляет собой геометрическую сумму вертикальных и горизонталь-

ных нагрузок, плоскость расположенbя провода будет наклонена к вертикали на не который угол β. Этот же угол β будет составлять равнодействующая нагрузка qx с

вертикалью. Если требуется установить для этого режима высоту провода от земли,

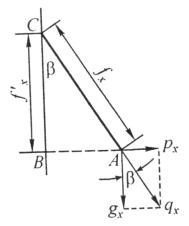
то нужно определить вертикальную проекцию стрелы провеса провода fx (рис. 3.26):

(3.44)

Решение кубического уравнения (3.42) можно произвести графическим спосо-

бом, придав ему вид Нх=Ах/Нх2 +Вх и находя точку пересечения прямой у = Нх и

кривой Нх=Ах/Нх2 +Вх. Однако на практике уравнение (3.42) обычно решают подбо-

ром, на что требуется несколько минут, причем может быть достигнута любая сте-

пень точности.

Рис. 3.26. Расчетная схема определения вертикальной составляющей стрелы провеса нити

Расчет стрел провеса провода при различных режимах. Если в уравнении

(3.41) заменить Н его значением из уравнения (3.19), то после несложных преобра-

зований получим

(3.45)

Решение этого уравнения может быть произведено тем же путем, что и уравне-

ние (3.41). После подстановки всех известных величин в уравнение оно получит вид

(3.46)

где

В уравнении (3.45) также можно заменить отношение q/S величиной γ, т.е. пе-

рейти к удельным нагрузкам.

Уравнения (3.41) и (3.45) дают возможность по известной величине стрелы провеса или натяжения для какого-либо режима температуры и нагрузки определить эти величины для любого другого режима, характеризуемого заданной нагрузкой и температурой. Таким образом, чтобы приступить к расчету, необходимо предвари-

тельно задаться какой-либо одной величиной (натяжением или стрелой провеса) для какого-либо режима. Это даст возможность перейти к любому другому режиму.

Прежде чем говорить о выборе этой исходной величины, нужно ясно предста-

вить сущность механического расчета подвески. Подвешивая провод, можно полу-

чать различные стрелы провеса, задаваясь различной величиной натяжения. Если основная задача подвески — подвод энергии к поездам при помощи перемещаю-

щихся токоприемников, то, как будет показано ниже, для улучшения процесса токо-

снимания нужно обеспечить возможно большее натяжение провода.

Даже в том случае, когда подвешиваемый провод не служит для снятия тока

(например, питающий провод, или провод ВЛ), часто целесообразно давать ему большее натяжение с целью уменьшения высоты опор, что во многих случаях сни-

жает стоимость подвески. В некоторых случаях, когда указанные условия не играют роли (на пример, если высота опор определяется другими факторами или использу-

ют готовые опоры, имеющие достаточный запас высоты), а также, когда нагрузка опор уменьшается при снижении натяжения, задаются максимально допускаемой стрелой провеса провода.

Независимо от того, какие условия будут положены в основу расчета, его про-

изводят не только для режимов, дающих наибольшее натяжение или наибольшие стрелы провеса, но и для ряда других режимов. Так, для определения отклонений подвески под действием ветра устанавливают величину натяжения в проводе при этом режиме. Учитывая, что монтаж подвески может происходить при различных температурах, производят расчеты для ряда режимов, обычно отличающихся один от другого температурой 5—10° С.

Получив ряд значений для натяжений и стрел провеса сводят эти данные в таб-

лицу или представляют их в виде кривых зависимости натяжения и стрел провеса от температуры. При монтаже подвески монтер или бригадир, производящий работу,

для каждой температуры выбирает соответствующее натяжение. Назначение этих кривых и таблиц определило их название – монтажные кривые и монтажные таб-

лицы.

Выяснив, что для большинства случаев желательно иметь в проводе возможно

большее натяжение, нужно определить, при каком из режимов натяжение достигает наибольшей величины. Как указывалось, увеличение натяжения провода может воз-

никнуть вследствие понижения температуры и повышения нагрузки (вес гололеда,

давление ветра).

Если изучение метеорологических условий района приведет к выводу, что при каком-либо режиме возможно совпадение всех указанных выше явлений, то, несо-

мненно, что наибольшее натяжение в проводе будет иметь место именно при этом режиме. Однако результаты наблюдений метеорологических станций в течение ряда лет свидетельствуют о том, что при наименьшей температуре воздуха обычно не бывает добавочной нагрузки. Это обстоятельство вносит в расчет не которую не-

определенность, так как заранее не представляется возможным указать, какой из режимов (режим наименьшей температуры или режим наибольшей добавочной нагрузки) нужно считать при расчете исходным, т.е. дающим в проводе наибольшее натяжение.

Предположив произвольно, что какой-либо из этих режимов даст наибольшее натяжение в проводе, можно принять его за исходный, т.е., допустив, что Н1 = Нmах

(Нmах — наибольшее натяжение, допускаемое по прочности провода), пользуясь формулой (3.41), можно найти Нх, где Нх и будет относиться ко второму тяжелому режиму. Возможно, что во втором режиме даст Нх>Н1 и, следовательно, больше до-

пускаемого. В этом случае необходимо произвести весь расчет сначала, взяв за ис-

ходный второй режим и предположив, что именно при этом режиме Н =Нmах, после чего определять по тем же формулам натяжения и стрелы провеса для других режи-

мов.

Этой неопределенности можно избежать, сравнивая длину за данного пролета с

«критическим», определение которого будет рас смотрено ниже.

Влияние длины пролета на изменение натяжения провода. Критический

пролет и критическая нагрузка. Если при каком-либо режиме провод имеет неко-

торое натяжение, то, как ясно из изложенного ранее, при изменении температуры и нагрузки величина натяжения изменяется.

При этом расчеты и практика показывают, что соотношение натяжения в про-