1. Барометрическая формула. Распределение Больцмана.

1) Газ находится в однородном поле тяжести.

2) Температура газа одинакова на любой высоте.

P – (P + dP) = ρ*g*dh

dP = -ρ*g*dh = - μ*g/(R*T)*P*dh

dp/p = -μ*g/(R*T)*dh

_p1∫^p2dP/P = _p1∫^p2(-μ*g/(R*T))*dh

lnP₂/P₁ = - μ*g/(R*T)*(h₂ – h₁)

барометрическая формула

P₀ – давление на уровне моря

h – высота над уровнем моря

m*g*h = W_p

n = n₀* e^(- W_p/(k*T)) – распределение Больцмана для поля потенциальных сил

2. Понятие о вырождении системы частиц.

Вырождение идеальных газов – отклонение их свойств от свойств обычных газов, вызываемое квантовыми свойствами системы.

Вырождение газов наблюдается при низкой температуре и большой плотности.

N/G ≈> 1

G – число состояний

N – число частиц в системе

Параметром вырождения называется величина:

h – постоянная Планка

n – концентрация молекул

m – масса молекул

T – температура

k – постоянная Больцмана

Билет №6.

1. Закон Максвелла о распределении молекул идеального газа по скоростям.

√(V²) = √(3*k*T/m) = √(3*R*T/μ) – средняя квадратичная скорость

f(V) – функция распределения молекул по скоростям, т.е. относительное число молекул, скорости которых лежат в интервале от V до V+dV.

df(V)/dV = 0

Vв = √(2*R*T/μ) – вероятная скорость

Vа = √(8*R*T/(π*μ)) – средняя арифметическая скорость

П

√(V²)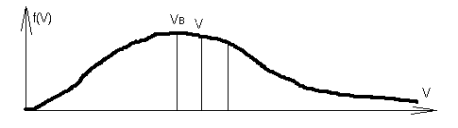

лощадь под кривой пропорциональна числу молекул. При повышении температуры максимум смещается вправо, а площадь остаётся постоянной.

2. Классическая теория теплоёмкости кристаллов. Закон Дюлонга и Пти.

C = dU/dT

Кристалл – система с 3N колебательными степенями свободы, на каждую из которых приходится E=k*T энергии.

U_μ = 3*N_A*E = 3*N_A*k*T

C_μ = 3R – закон Дюлонга и Пти – молярная теплоёмкость химически простых кристаллов равна 3R.

Билет №7.

1. Вероятная, средняя арифметическая и средняя квадратичная скорости.

√(V²) = √(3*k*T/m) = √(3*R*T/μ) – средняя квадратичная скорость

f(V) – функция распределения молекул по скоростям, т.е. относительное число молекул, скорости которых лежат в интервале от V до V+dV.

Vв = √(2*R*T/μ) – вероятная скорость

Vа = √(8*R*T/(π*μ)) – средняя арифметическая скорость

2. Понятие о квантовой теории теплоёмкости Эйнштейна и Дебая.

Эйнштейн:

Частицы совершают колебания около узлов кристаллической решётки, но энергия гармонического осциллятора изменяется не непрерывно, а дискретно.

E = ћω

Средняя энергия квантового осциллятора:

При больших температурах энергия равна энергии кристалла в представлении Дюлонга и Пти.

Дебай:

Каждому колебанию соответствует стоячая волна.

Минимальная порция энергии, которую может поглотить или испустить кристаллическая решётка, называется фононом (квант тепла).

h*ν_max = ћ*ω_max

h*ν_max = k*θ_Д

θ_Д = hν_max/k – температура, выше которой в кристалле осуществляются колебания со всеми возможными частотами, т.е. существуют все возможные фононы.

С_T->0 = β*T³ – закон кубов Дебая.

Билет №8.

1. Распределение молекул по кинетическим энергиям. Распределение Максвелла-Больцмана.

Функция распределения молекул по энергиям теплового движения определяет относительное число молекул из общего числа N молекул, которые имеют данную кинетическую энергию .

распределение Максвелла-Больцмана

2. Теплоёмкость электронного газа в металлах.

При повышении температуры металла тепловому воздействию подвергаются не все электроны, а лишь незначительная часть.

Для невырожденного электронного газа:

В металлах электронный газ вырожден.

Поглощают тепло не все электроны, поэтому теплоёмкость металла в целом равна теплоёмкости его решётки.

Билет №9.

1. Среднее число столкновений и средняя длина пробега.

Длина свободного пробега – расстояние, проходимое частицей между двумя последовательными столкновениями.

Эффективный диаметр молекулы – наименьшее расстояние, на которое сближаются центры молекул при соударениях (d).

- эффективное сечение молекулы.

Среднее число соударений в единицу времени:

Средняя длина свободного пробега:

при T=const :

2. Классическая электронная теория электропроводности металлов.

Авторы – Друде и Лоренц.

1) Электроны представляют собой молекулы идеально газа.

2) После соударения с ионом, электроны полностью теряют кинетическую энергию.

3) Длина свободного пробега для всех электронов одинакова.

– закон Ома

, где j – плотность тока, е – заряд электрона, n – концентрация, – средняя скорость направленного движения электронов.

– удельная электропроводность

Билет №10.

1. Явление переноса. Диффузия.

Диффузия – распространение молекул примеси от места их введения при отсутствии макроскопических перемещений.

- закон Фика

Поток вещества пропорционален градиенту концентрации и направлен в сторону уменьшения концентрации.

2. Понятие о квантовой теории электропроводности металлов.

Электрон – плоская волна де Бройля, поэтому прохождение электрона через кристаллы можно сравнивать с прохождением волны.

В идеальной решётке наблюдается только преломление, т.е. изменение физическорй скорости.

Для рассеивания в идеальной решётке необходимо наличие дефектов, включая тепловые колебания.

(Зоммерфельд:)

- средняя длина свободного пробега жлектронов, обладающих энергией Ферми

– скорость такого электрона; не зависит от «Т».

η_Т – коэффициент рассеивания

E – модуль упругости

d – параметр решётки

ρ

ρ_L T

ρ_L – удельное сопротивление, обусловленное структурным дефектом

ρ_Т – удельное сопротивление, обусловленное температурными колебаниями

ρ

Т_к Т

Сверхпроводимость – исчезновение электрического сопротивления у некоторых металлов и сплавов при T<T_к, т.е. температуры перехода в сверхпроводящее состояние.

Билет №11.