Дифференцирование функции от функции (Цепное правило).

237. Применив цепное правило вычислить производные функций

;

;

23)

238. Используя калькулятор, вычислить производные функций в заданной точке

239. Найти производную функции

1) 2)3)

240. Используя равенства

доказать формулы

Логарифмическое дифференцирование

241. Вычислить производные заданных функций

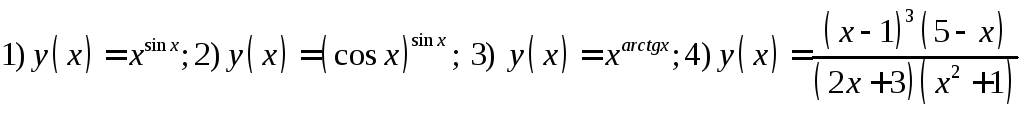
Формулы неявного дифференцирования

242. Доказать, что данные формулы задают одну и туже кривую линию

243. Применяя правило неявного дифференцирования, вычислить

производные от функций заданных неявно (уравнениями)

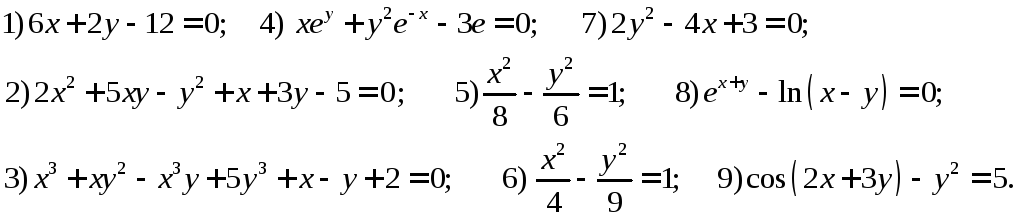
244. Найти вторую производную функциизаданной

неявно (уравнениями)

;

Формулы параметрического дифференцирования

245. Вычислить и записать в параметрическом виде производные от

функциизаданной в параметрическом виде

246. Вычислить и записать в параметрическом виде первую и вторую производные

иот функцийзаданных в параметрическом виде

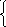
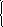
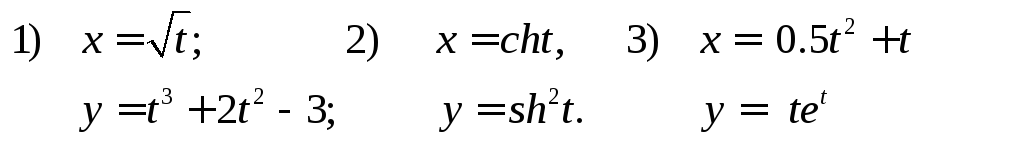4)

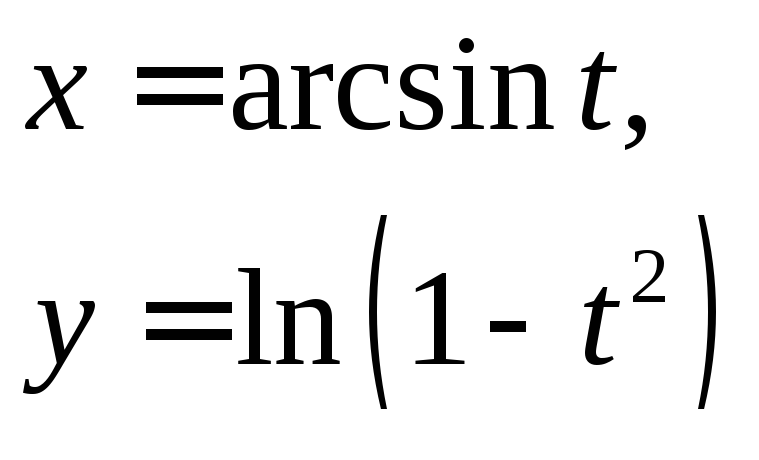
246. Написать уравнение касательной и нормали к кривым заданным

неявно (уравнениями) в точке

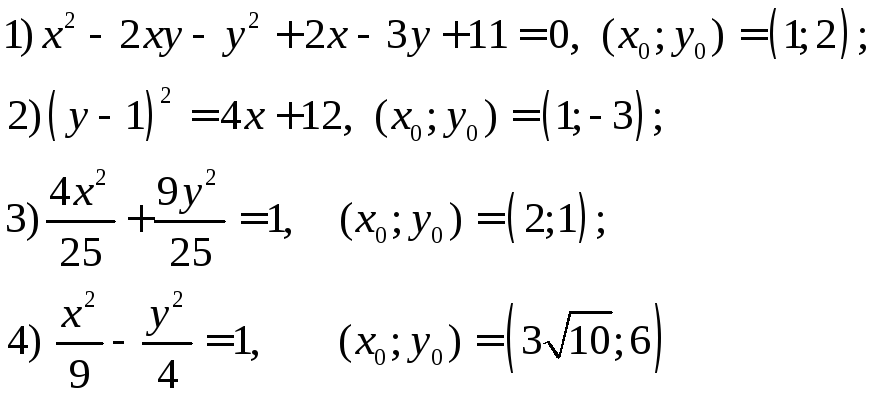
246. Написать уравнение касательной и нормали к кривым заданным

параметрическими уравнениями

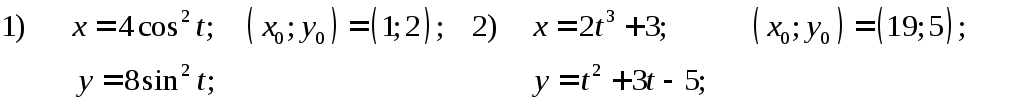
Дифференциал функции

249. Используя таблицу найти дифференциалы следующих функций

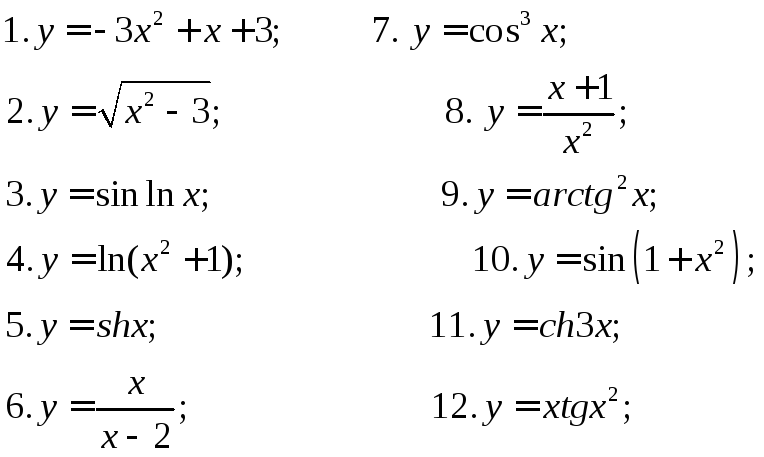
250. Пусть Проверить справедливость равенства

251. Изобразить геометрически приращение функции и дифференциал функции

при заданных величинах . Оценить погрешность по графику

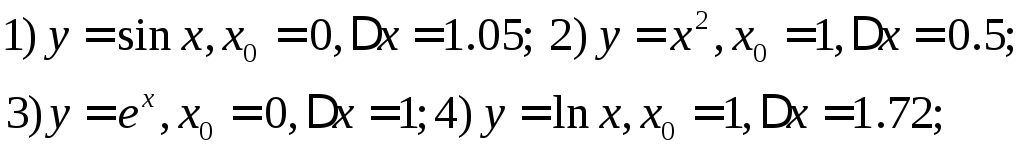
252. Используя понятие дифференциала получите приближённые формулы,

справедливые для малых

1) 2)3)4)5)

253. Используя формулу линейного приближения функции , оценить максимальную погрешность при вычислении значения выражения , при,если аргументзадан приближённо.

254. Используя формулу линейного приближения функции , оценить максимальную

погрешность при вычислении значения выражения, при,если

аргумент задан приближённо.

255. Вычислить значение данного выражения двумя способами: а) используя

калькулятор и в) используя формулу линейного приближения функции

1)(взять) 3)(взять)

2) (взять); 4)(взять;;

).

256. Приближенно измеренный радиус круга оказался равным м.

Используя формулу линейного приближения , оценить какова будет максимальная ошибка при вычислении

1) площади круга, 2) длины окружности.

257. Приближенно измеренный радиус шара оказался равным 1м.

используя формулу линейного приближения , оценить какова будет

максимальная ошибка при вычислении площади поверхности ()

этого шара. Для расчётов взять .

258. Приближенно измеренное ребро куба оказался равным м. Используя

формулу линейного приближения, оценить какова будет максимальная ошибка при

вычислении объёма куба и площади поверхности куба.