
- •Новосибирский государственный архитектурно- строительный
- •Определители
- •Матрицы.
- •Кривые в полярной системе координат.
- •Элементы векторной алгебры
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов.
- •Плоскости и прямые в пространстве
- •Введение в математический анализ
- •Предельные значения функции
- •Непрерывность и разрывы функций
- •Замечательные пределы
- •Дифференцирование функции от функции (Цепное правило).
- •Правило Лопиталя
- •Исследование функций и построение их графиков
- •Задачи на нахождение наибольших и наименьших значений функций
- •Кривизна дуги кривой.
- •93.1 93.2
- •173.1 173.2173.3 173.4
- •212.1 212.2
- •212.3212.4
- •220.1 220.2220.3220.4
- •294.1 294.2
Задачи на нахождение наибольших и наименьших значений функций
Число 8 разбить на два слагаемых так, чтобы их произведение было
наибольшим.
Найти на оси
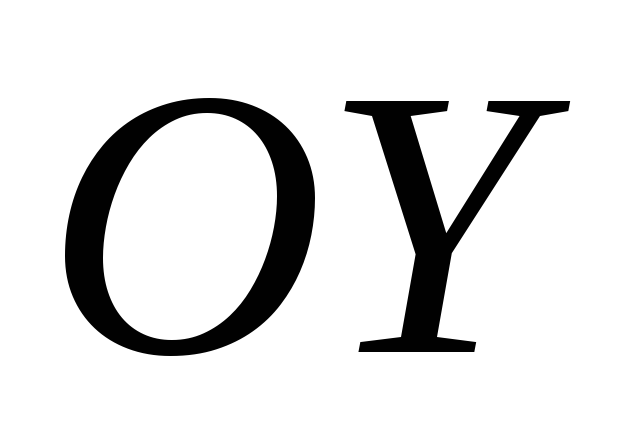 точку,
для которой сумма квадратов расстояний
от точек
точку,
для которой сумма квадратов расстояний
от точек
![]() была
бы наименьшей.
была
бы наименьшей.
Среди прямоугольников, имеющих периметр 8м, найти прямоугольник
с наибольшей площадью.
Среди прямоугольных треугольников, имеющих одинаковую гипотенузу
![]() =10м,
найти треугольник наибольшей площади.
=10м,
найти треугольник наибольшей площади.
Прочность балки прямоугольного сечения прямо пропорциональна ширине
балки и квадрату её высоты. Определить параметры балки наибольшей
прочности, которую можно вырезать из бревна, диаметр которого 0.5м.
Пусть требуется построить цилиндрический бак объёмом
 .
Какими
.
Какими
должны быть размеры бака, чтобы на его изготовление ушло как можно
меньше листовой стали. Для расчётов
принять
![]() .
.
Из стального листа площадью
 требуется
изготовить цилиндр
требуется
изготовить цилиндр
наибольшего объёма. Определить радиус и высоту такого цилиндра.
Для расчётов принять
![]() .
.
Среди всех прямых круговых конусов, у которых образующая равна
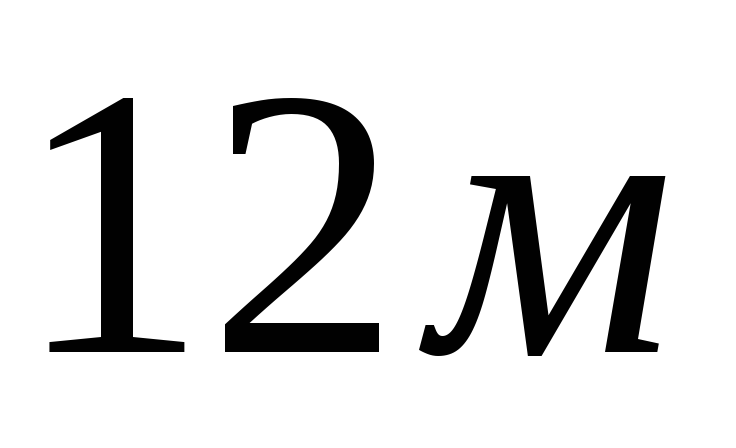 ,
,
найти радиус основания конуса наибольшего объёма.
Кривизна дуги кривой.
Найдите кривизну следующих линий
![]()
Вычислите кривизну линий в точке
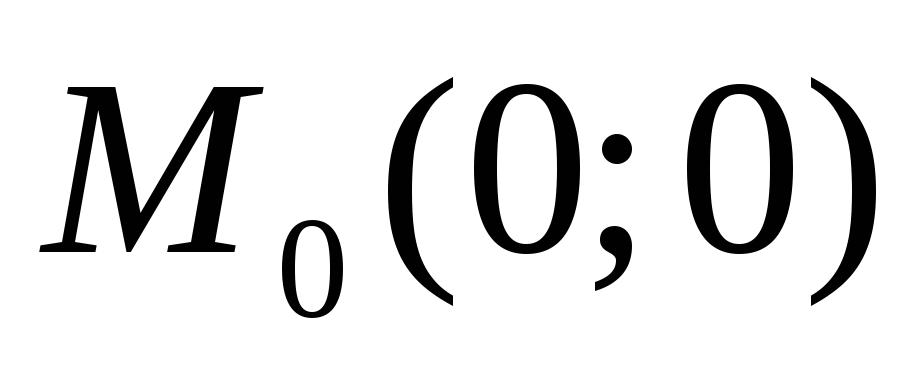
![]()
Найдите кривизну следующих линий
![]()
306. Найдите кривизну линий, заданных параметрическими уравнениями
![]()
ОТВЕТЫ И РЕШЕНИЯ.
Определители.
1.1 17 1.2 01.3 1 2.1 -12.2
12.3 13.1 93.2 -263.3 -214.0
![]()
4.1
 4.2
4.2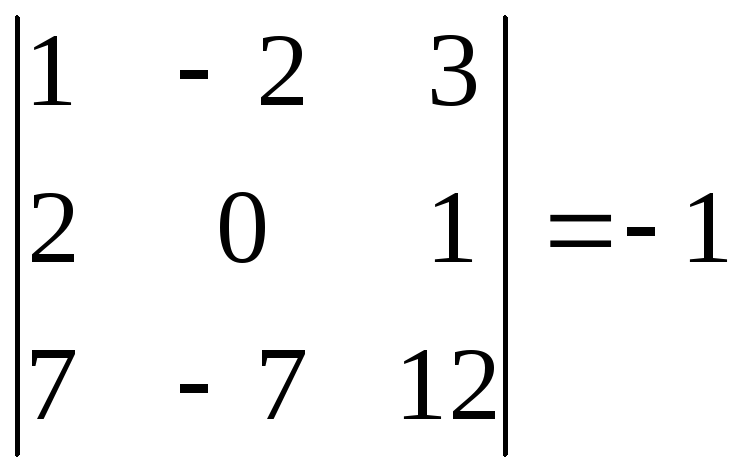 5.
5.![]() так как в каждом определителе есть
одинаковые строки.
так как в каждом определителе есть
одинаковые строки.
Матрицы.
6.1
![]() ;
;![]()
6.2
![]()
![]()
![]()
7.1 ![]() 7.2
7.2 ![]() 7.3
7.3 ![]()
8.Нельзя. Матрицы разных размерностей.
9. 1 ![]() 9.2
9.2
 9.3
9.3![]() 9.4
9.4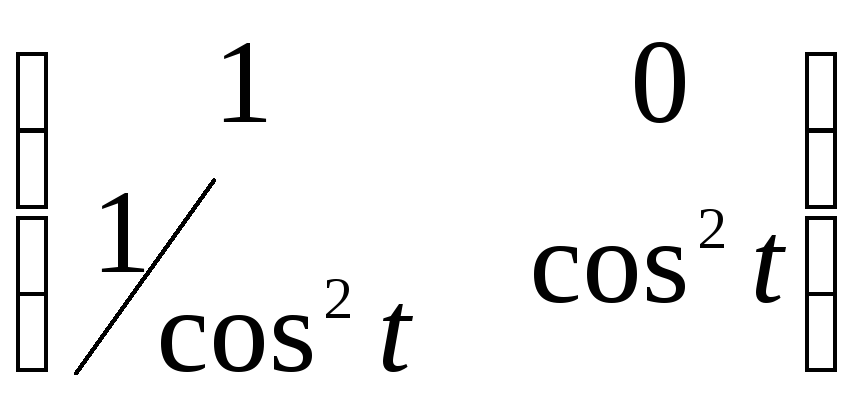
10.
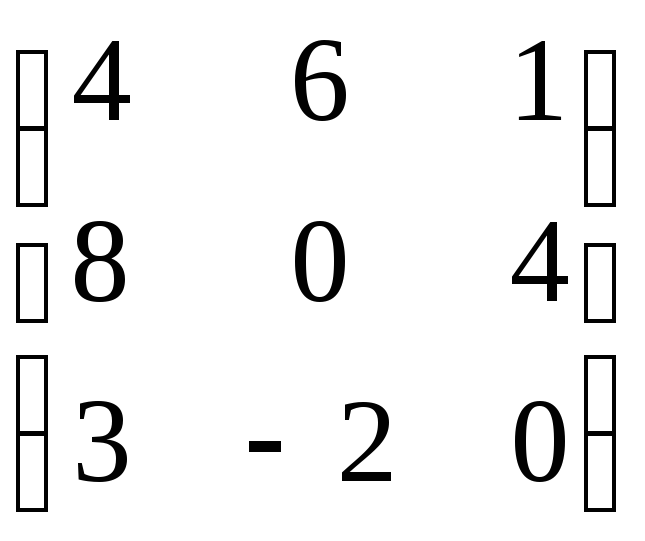 11.
11.
![]()
12.
 ;
;
![]() - не существует.
- не существует.
13.1![]() 13.2
13.2![]() 13.3
13.3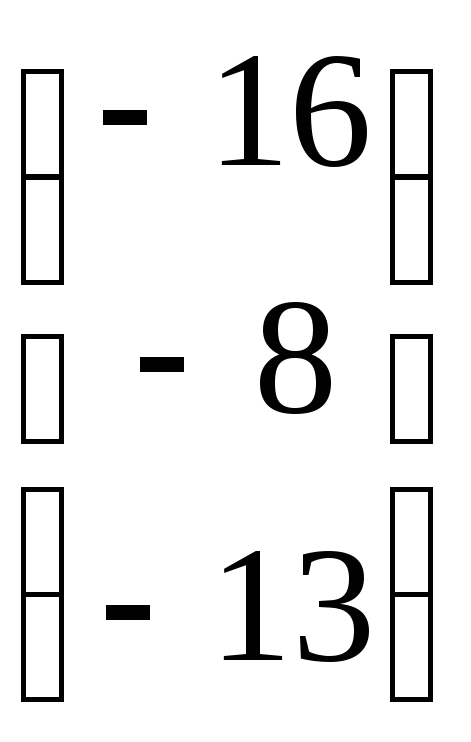 13.4
13.4![]() 13.5
13.5![]() не
существует.
не
существует.
13.6
![]() 13.7
13.7![]() 14.1
14.1![]() 14.2
14.2![]() 14.3
14.3![]()
15.1
![]()
15.2
![]()
![]()
![]()
15.3
![]()
![]()
![]()
16.1 -3, 5 16.2 -3, 216.3-3, 2.17.
![]() ,
,![]()
![]()
![]()
18.
![]() 19.
19.![]() 20.Не являются.
20.Не являются.
21. Матрица![]() имеет обратную матрицу.
имеет обратную матрицу.
22.1
![]() 22.2
22.2![]() 22.3
22.3
23.1
![]() 23.2
23.2 23.3
23.3 23.4
23.4![]()
23.5
 24.1
24.1![]() 24.2
24.2![]()
25.1
![]() 25.2
25.2![]()
Системы линейных алгебраических уравнений.
26. Не являются.27. Являются.
28.1
![]() 29.1
29.1![]() 29.2
29.2![]()
30.1


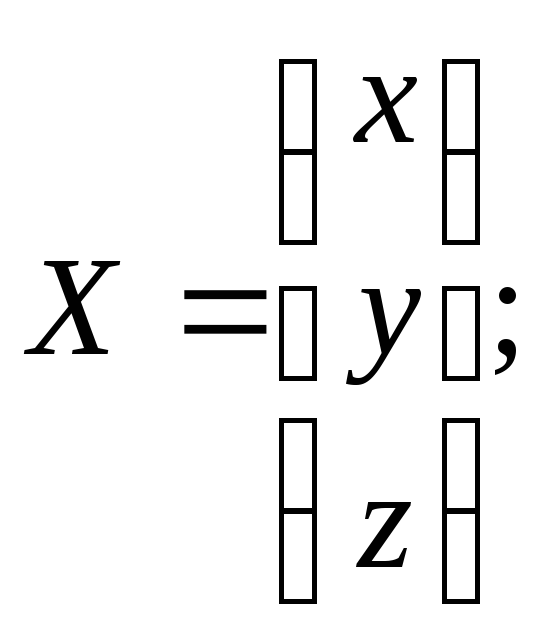
![]()
30.2
![]() где
где

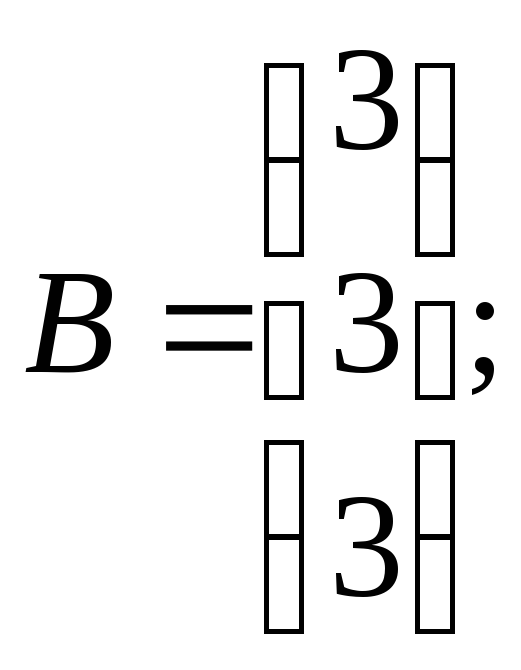
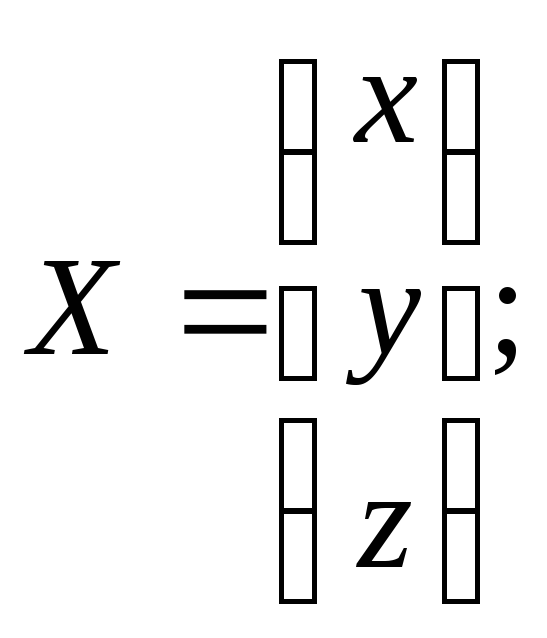
30.3
![]() где
где
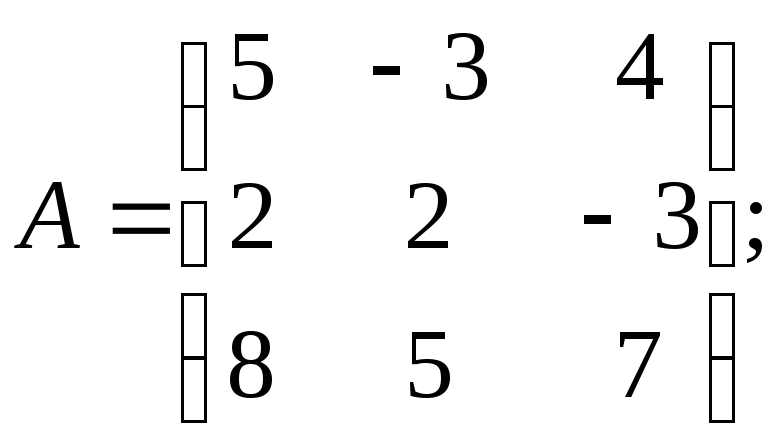

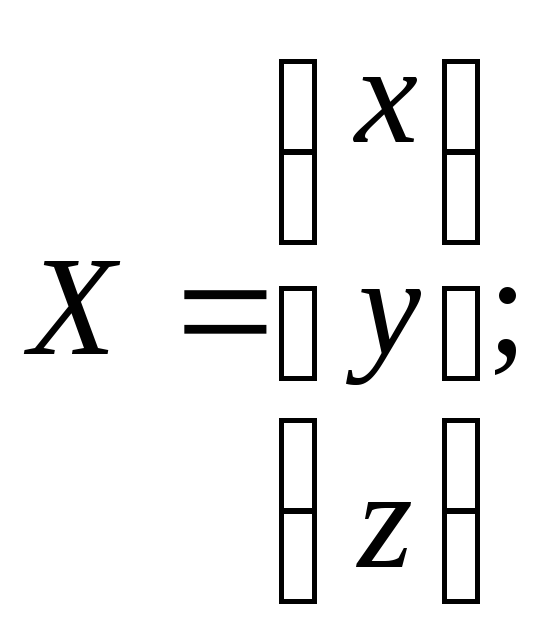
31.1
![]()
![]() 31.2
31.2![]()
![]()
31.3
![]()
![]() 31.4
31.4![]()
![]()
31.5

 32.1
32.1![]()
![]()
![]()
![]() 32.2
32.2
![]()
![]()
![]()
![]()
![]()
![]()
33.1
![]()
![]()
![]() 33.2
33.2![]()
![]()
![]() 33.3Система не совместна33.4
33.3Система не совместна33.4
![]()
![]()
![]()
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ГАУССА.
34.1
 34.2
34.2
34.3
 35.1
35.1![]() 35.2
35.2![]() 35.3
35.3
35.4
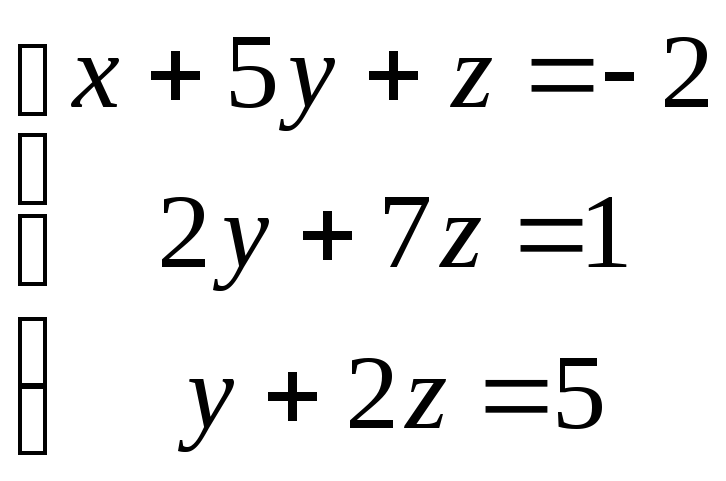 36
36![]()
![]() ;
;![]() Решения одинаковы.
Решения одинаковы.
37.1
![]()
![]()
![]() 37.2
37.2![]()
![]()
![]() 37.3
37.3![]()
![]()
![]() 38.1
38.1![]()
![]()
![]() 38.2
38.2![]()
![]()
![]()
38.3 Система не совместна.39.1
![]()
![]()
![]()
39.2
![]()
![]()
![]()
![]() 39.3
39.3
![]()
Элементы векторной алгебры и аналитической геометрии.
Прямая линия на плоскости.
40.
![]() 41.
41.![]() 42.1
42.1![]() 42.2
42.2![]() 42.3
42.3![]()
42.4
![]() 42.5
42.5![]() 42.6
42.6![]()
42.7
![]() 43.1
43.1![]() 43.2
43.2![]() 43.3Обе точки принадлежат прямой.
43.3Обе точки принадлежат прямой.
44.1
![]() 44.2
44.2![]() 44.3
44.3![]() 44.4
44.4![]() 45.1
45.1![]() 45.2
45.2![]() 45.3
45.3![]() 45.4
45.4![]()
46.1 46.2


46.4
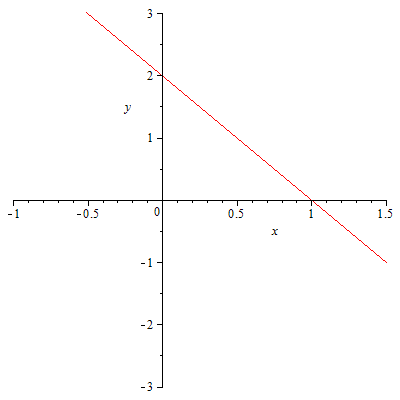

46.5

47.1
![]()
![]() 47.2
47.2![]()
![]()
47.3
![]()
![]() 47.4
47.4![]() 48.
48.![]()
![]()
49.1
![]() 49.2(0.5; 1).
49.2(0.5; 1).

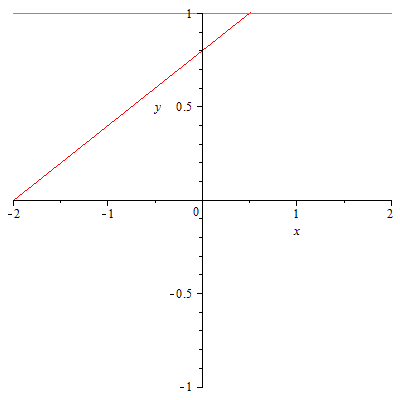

49.3 (2; 2).50.![]()
51.
![]()
![]()
![]()
![]()
![]()
![]()
52.1
![]()
![]()
![]()
52.2
![]()
![]()
![]()
52.3
![]()
![]()
![]()
53.
![]() А1 –выше; А2 –на
прямой;
А1 –выше; А2 –на
прямой;
А3 – ниже; А4 –выше; А5 –ниже;
А6 – на прямой.
54.
![]()
![]()
55.
![]() 56
56![]()
![]()
![]()
57
![]() 58.
58.![]() 59.1
59.1![]() 59.2
59.2![]()
59.3
![]() 59.4
59.4![]() 59.5
59.5![]() 59.6
59.6![]()
59.7
![]()
![]() 60.
60.![]() -точка
пересечения перпендикуляра, проходящего
через точку М, с заданной прямой.
-точка
пересечения перпендикуляра, проходящего
через точку М, с заданной прямой.![]()
Кривые второго порядка.
Парабола.
61.
![]()
62.1
![]() 62.2
62.2![]()

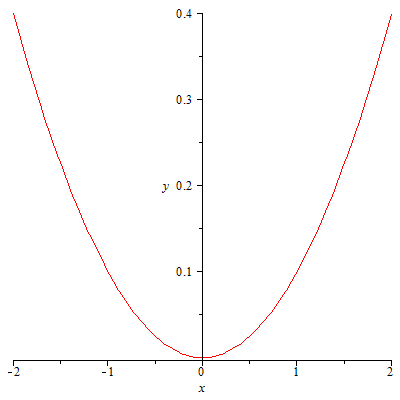
62.3
![]() 62.4
62.4![]()
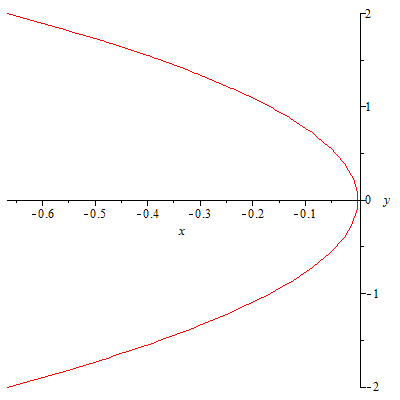
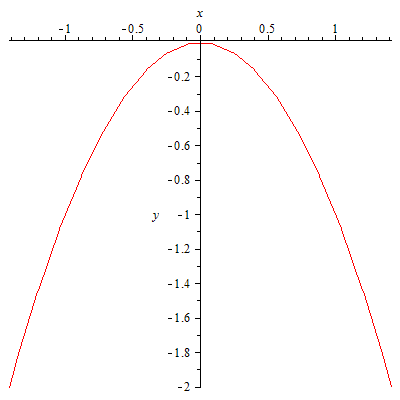
63.1
![]()
![]()
![]() 63.2
63.2![]()
![]()
![]()


63.3
![]()
![]()
![]() 63.4
63.4![]()
![]()
![]()
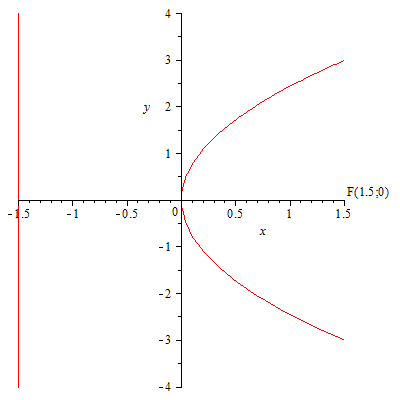
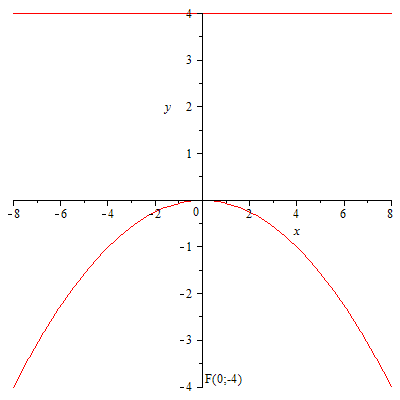
64.
![]() 65.
65.![]() 66.
66.![]() .
67.1
.
67.1![]() 67.2
67.2![]()
68.1
![]() 68.2
68.2![]() 69.1
69.1![]() 69.2Точек нет.
69.2Точек нет.
Окружность.
70.1
![]() 70.2
70.2![]() 71.
71.![]()
![]()
![]()
![]()
Эллипс.
72.1
![]() 72.2
72.2![]() 72.3
72.3![]() 72.4
72.4![]()
73.1
![]() 73.2
73.2![]() 73.3
73.3![]() 73.4
73.4![]()
74.
![]()
![]()
![]()
![]()
![]()
![]()
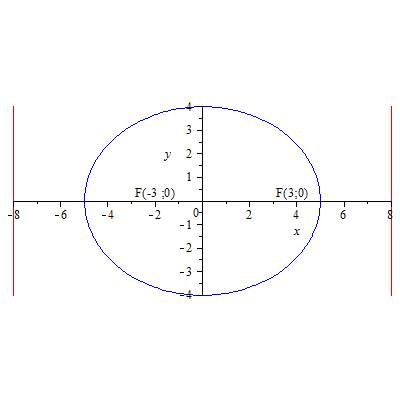
75.1 75.2

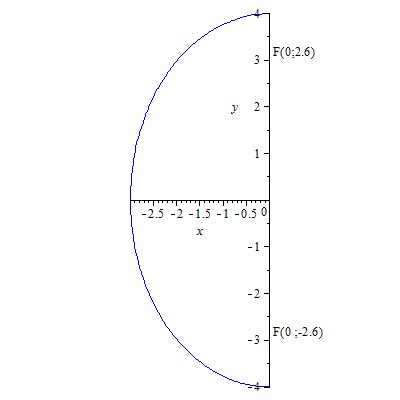
Эллипс.
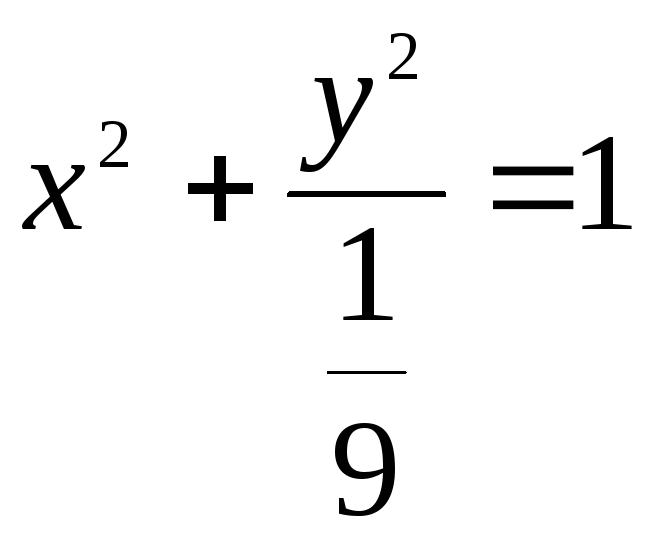 77. Эллипс
77. Эллипс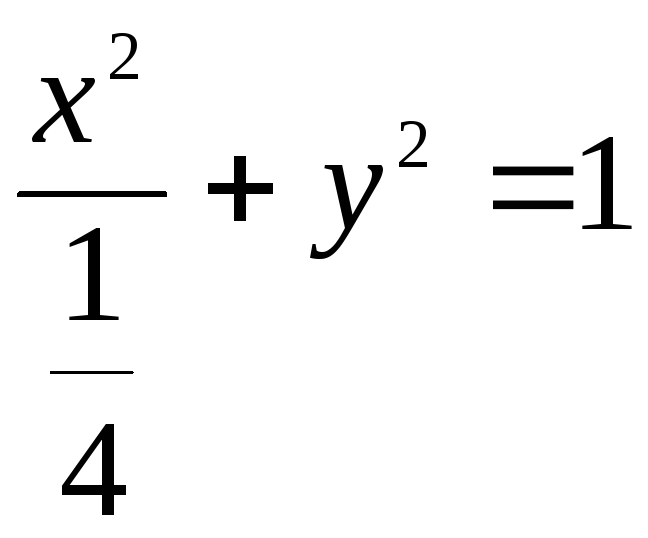
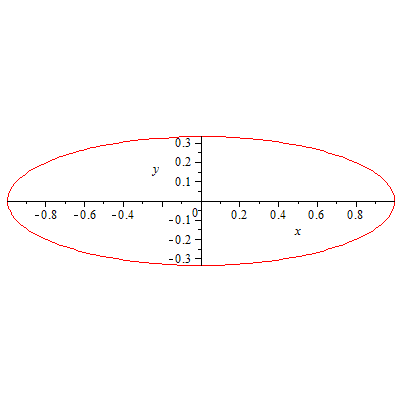
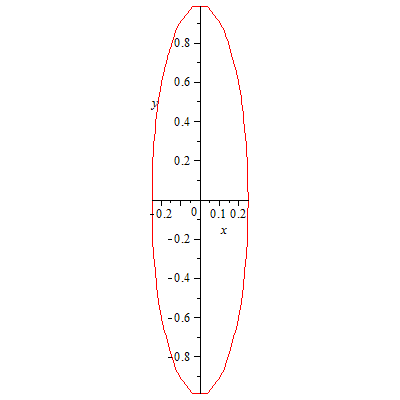
78.
![]()
![]() 79.
79.![]()
![]()
Гипербола.
80.1
![]() 80.2
80.2![]()
![]()
 80.3
80.3
![]()
80.4
![]()
![]()
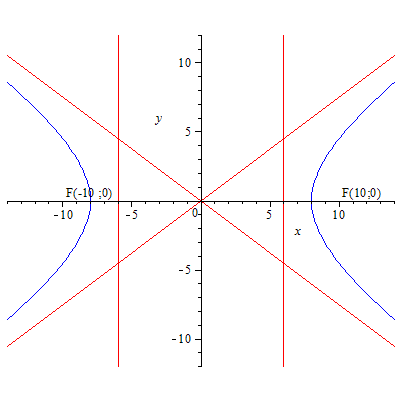
81.1
![]()
81.2
![]()
![]()
 81.3
81.3
![]()
81.4
![]()
![]()
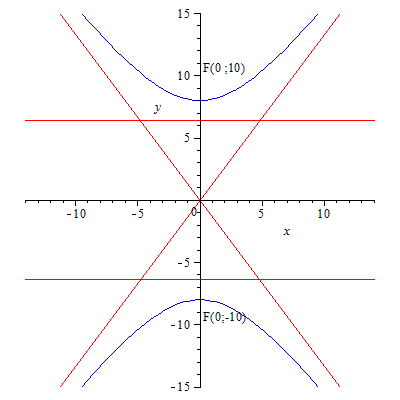
82.1 На оси Оу.82.2 На оси Ох. 82.3 На оси Ох.82.4 На оси Оу. 82.5 На оси Ох. 82.6 На оси Оу.
83.
![]()
![]()
![]()
![]()
![]()
![]()

84. Эллипс.![]()
![]()
![]() 85. Гипербола.
85. Гипербола.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
асимптоты:
.
асимптоты:![]()
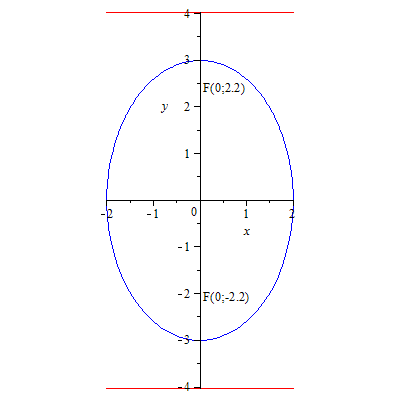

86. Парабола.![]()
![]() директриса:
директриса:![]() 87.1Гипербола.
87.1Гипербола.


87.2Гипербола87.3Гипербола

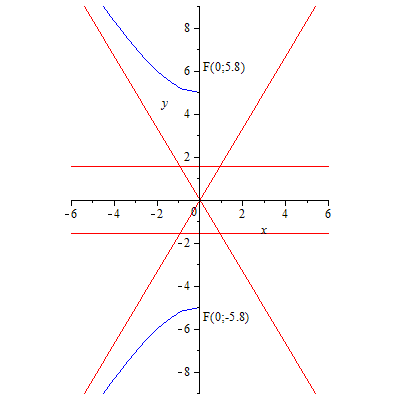
87.4 Гипербола.
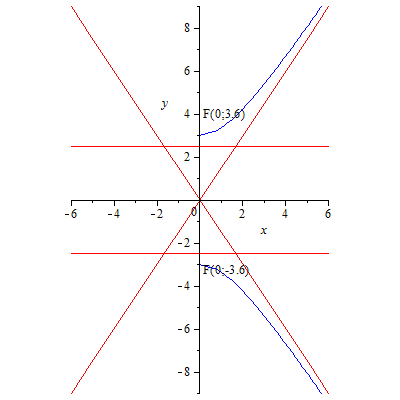
Кривые в полярной системе координат
89
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
90.1 х=2,у=0.90.2
![]()
![]() 90.3
90.3
![]()
![]() 90.4
90.4 ![]()
![]() 90.5
90.5
![]()
![]() 90.6
90.6
![]()
![]() 90.7
90.7 ![]()
![]() 90.8
90.8
![]()
![]() 90.9
90.9
![]()
![]() 90.10
90.10
![]()
![]()
91.

92.1 При замене
![]() ,
,![]() уравнение
уравнение
![]()
92.2 1 При замене
![]() ,
,![]() уравнение
уравнение
![]()
92.3 Парабола.![]()
![]()
![]() Формулы перехода:
Формулы перехода:![]()
![]() полярная ось направлена вдоль оси Ох;
полюс совпадает с фокусом. При подстановке
в уравнение получаем
полярная ось направлена вдоль оси Ох;
полюс совпадает с фокусом. При подстановке
в уравнение получаем![]() или
или![]() ,
или
,
или![]() .
Разрешая это уравнение относительно
.
Разрешая это уравнение относительно![]() получаем
получаем![]() каноническое уравнение параболы в
полярной системе координат.
каноническое уравнение параболы в
полярной системе координат.
92.4 Парабола.![]()
![]()
![]() Формулы перехода:
Формулы перехода:![]()
![]() полярная ось направлена вдоль оси Оу в
противоположную сторону. При подстановке
в уравнение получаем
полярная ось направлена вдоль оси Оу в
противоположную сторону. При подстановке
в уравнение получаем![]() или
или![]() или
или![]() .
Решая это уравнение относительно
.
Решая это уравнение относительно![]() получим
получим![]() каноническое уравнение параболы в
полярной системе координат.
каноническое уравнение параболы в
полярной системе координат.
92.5 Эллипс, вытянут вдоль оси
Оу.![]()
![]()
![]()
![]()
![]()
![]() Формулы перехода:
Формулы перехода:![]()
![]() полярная ось направлена вдоль оси Оу
и совпадает по направлению. Полюс в
фокусе
полярная ось направлена вдоль оси Оу
и совпадает по направлению. Полюс в
фокусе![]() . При подстановке в уравнение получаем
. При подстановке в уравнение получаем
![]() Приводим к общему знаменателю и
освобождаемся от
Приводим к общему знаменателю и
освобождаемся от![]() ,
получаем
,
получаем![]() или
или![]() .
Решая это уравнение относительно
.
Решая это уравнение относительно ![]() получим
получим![]() - каноническое уравнение эллипса в
полярной системе координат . 92.6
Гипербола.
- каноническое уравнение эллипса в
полярной системе координат . 92.6
Гипербола.![]()
![]()
![]()
![]()
![]()
![]() Формулы перехода:
Формулы перехода:![]()
![]() полярная ось направлена вдоль оси Ох
и совпадает с ней по направлению. При
подстановке в уравнение получаем:
полярная ось направлена вдоль оси Ох
и совпадает с ней по направлению. При
подстановке в уравнение получаем: Приводим к общему знаменателю
и освобождаемся от
Приводим к общему знаменателю
и освобождаемся от![]() ,
получаем
,
получаем![]() или
или![]() . Решая это уравнение относительно
. Решая это уравнение относительно![]() получим
получим
![]() -каноническое уравнение гиперболы
в полярной системе координат.
-каноническое уравнение гиперболы
в полярной системе координат.
