
- •Новосибирский государственный архитектурно- строительный
- •Определители
- •Матрицы.
- •Кривые в полярной системе координат.
- •Элементы векторной алгебры
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов.
- •Плоскости и прямые в пространстве
- •Введение в математический анализ
- •Предельные значения функции
- •Непрерывность и разрывы функций
- •Замечательные пределы
- •Дифференцирование функции от функции (Цепное правило).
- •Правило Лопиталя
- •Исследование функций и построение их графиков
- •Задачи на нахождение наибольших и наименьших значений функций
- •Кривизна дуги кривой.
- •93.1 93.2
- •173.1 173.2173.3 173.4
- •212.1 212.2
- •212.3212.4
- •220.1 220.2220.3220.4
- •294.1 294.2
Предельные значения функции
186. Пусть переменная
![]() удовлетворяет неравенству
удовлетворяет неравенству
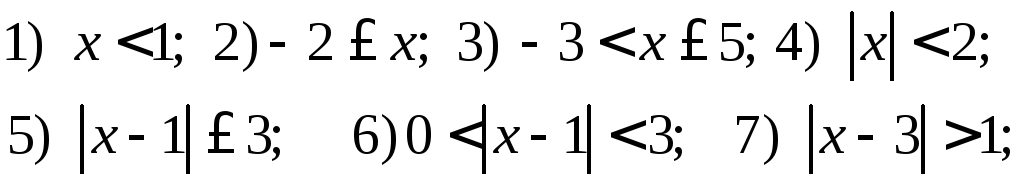
На числовой прямой укажите
интервалы, которым принадлежит
переменная![]() .
.
187. Пусть
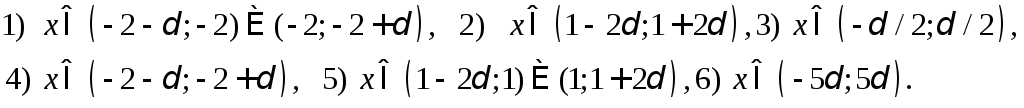
а) К какому числовому значению
стремится переменная
![]() ,
если параметр
,
если параметр![]()
неограниченно уменьшается до нуля.
б) В каком из случаев1)-6)
![]() может
принимать это предельное значение.
может
принимать это предельное значение.
188.
Пусть абсцисса графика функции
![]() стремится:
1) к
стремится:
1) к ![]() слева,
2) к
слева,
2) к ![]() справа
справа
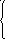
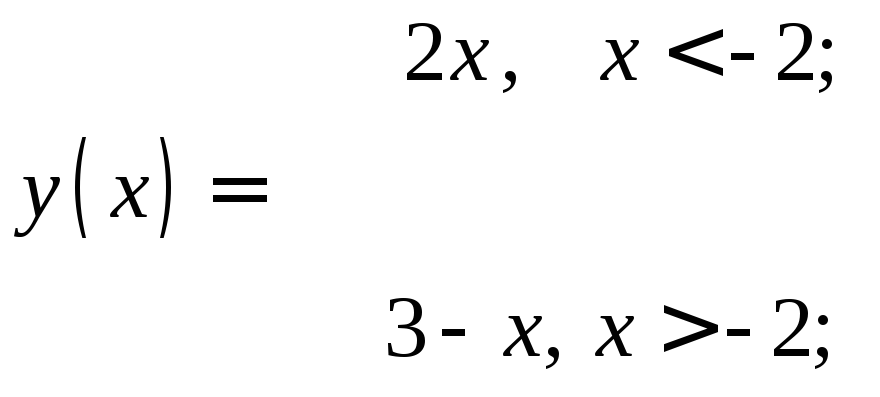
Определить по графику
![]() .
Существует ли
.
Существует ли![]()
Пусть аргумент
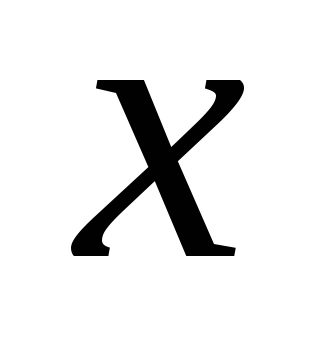 функции
функции стремится
слева к точке
стремится
слева к точке ,
принимая значения:
,
принимая значения:
![]() .
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
.
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции ![]() , если
, если
![]()
Пусть аргумент
 функции
функции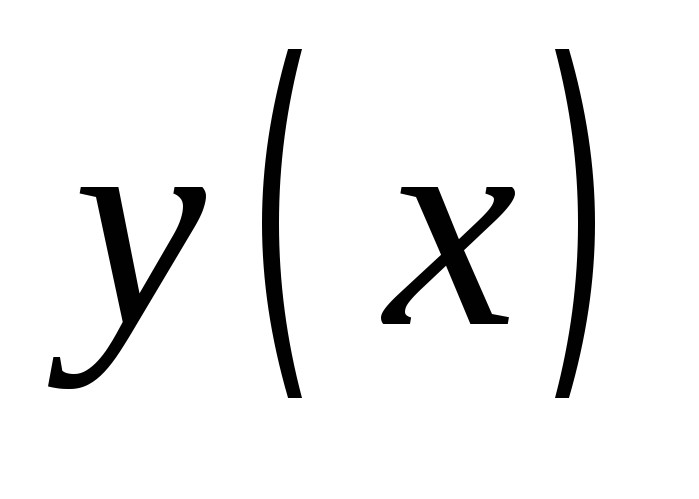 стремится
справа к точке
стремится
справа к точке ,
принимая значения:
,
принимая значения:
![]() .
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
.
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
![]() , если
, если
![]()
Проверить, используя график, функции: существует ли предельные значения данных функций
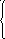
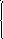

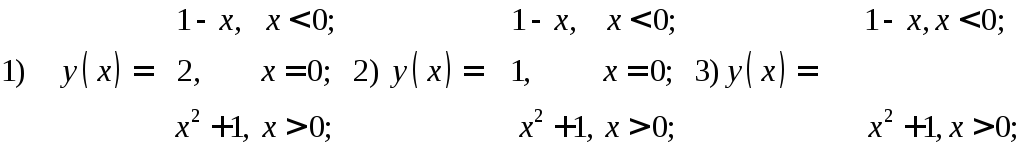
при стремлении аргумента![]() к 0.
к 0.
192. Пусть ![]()
Вычислить
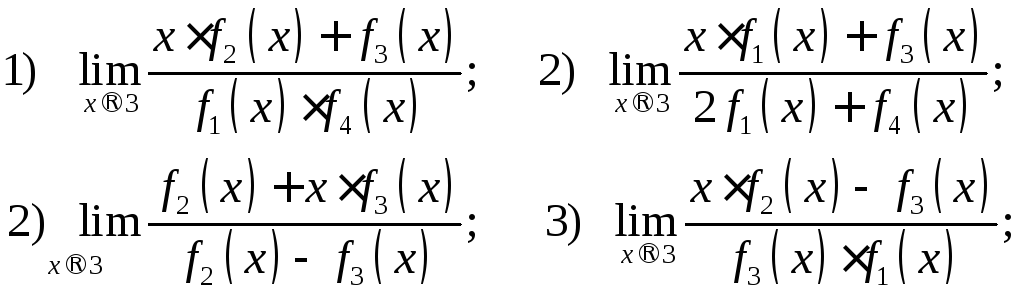
193. Пусть ![]()
Вычислить
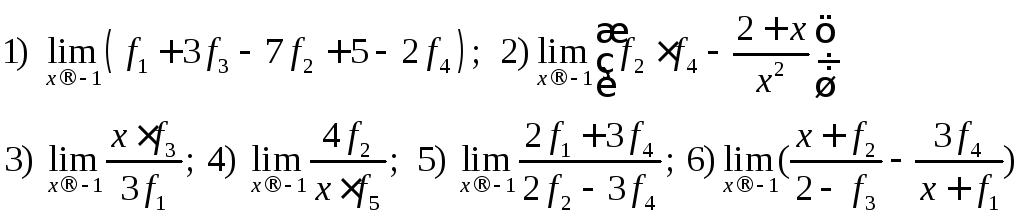
194. Пусть
![]() .
.
Вычислить

195. Используя график функции вычислить приближенно значения функций, левые и
правые предельные значения
функций в точке![]()
1)![]() 2)
2)![]() 3)
3)![]()


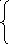

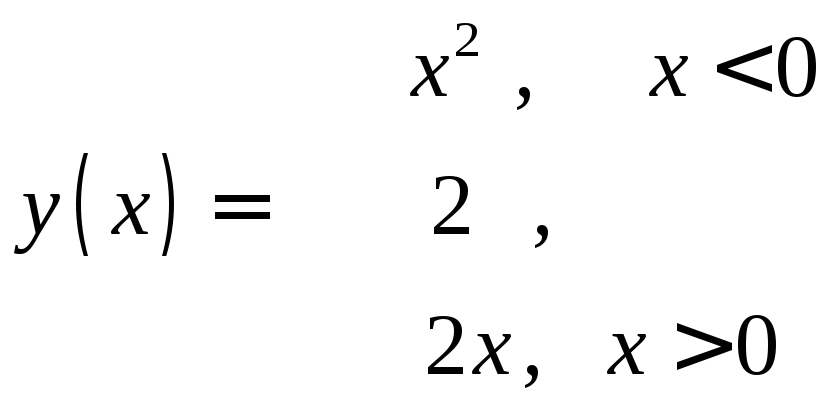

196. Пусть
![]() .
Вычислить предельные значения
.
Вычислить предельные значения
![]() .
.
197. Пусть
![]() .
Вычислить предельные значения
.
Вычислить предельные значения
![]() .
.
198. Пусть
![]() .
Вычислить предельные значения
.
Вычислить предельные значения
![]() .
.
Вычислить левые и правые предельные значения следующих функций.
![]()
При вычисления следующих пределов используйте правило
Правило 1. Для любой элементарной
функции
![]() справедлива
формула если
справедлива
формула если![]() ,то
,то
![]() ;
;
200. Вычислить указанные пределы и значения функции в предельных точках

![]()
201. Вычислить указанные пределы

202. Вычислить указанные пределы

203. Вычислить
указанные пределы 
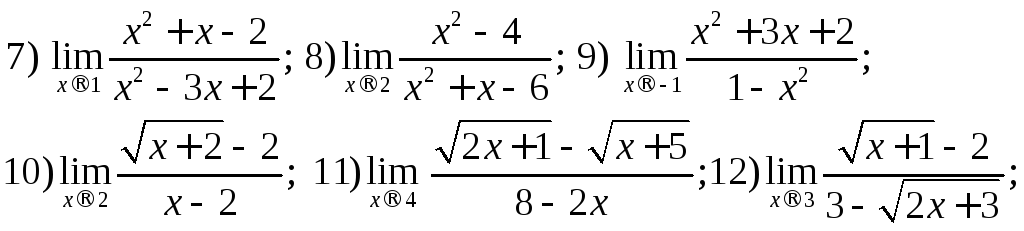
204.
Вычислить
![]() где
где
![]()
205.
Вычислить односторонние пределы в
точке![]() функций
функций
1)![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
Непрерывность и разрывы функций
206. Пусть функции
![]() определены на интервале
определены на интервале![]() и их сумма
и их сумма![]() и их разность
и их разность![]() являются
непрерывными функциями. Доказать, что
тогда функция
являются
непрерывными функциями. Доказать, что
тогда функция![]() является непрерывной.
является непрерывной.
207. Указать интервалы на оси ОХ, в которых данные функции непрерывны

Ответ обосновать.
208. При каком значении параметра
![]() данные функции
данные функции![]() непрерывны
непрерывны
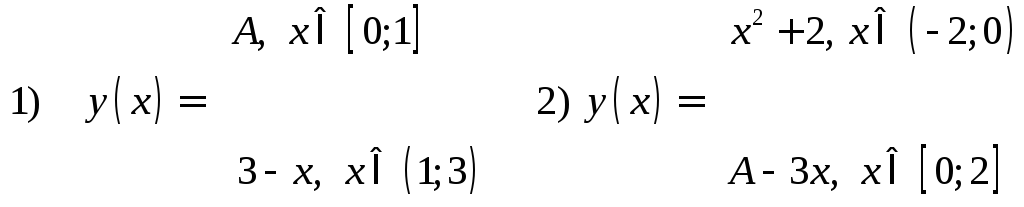

209. Исследовать данные функции на непрерывность
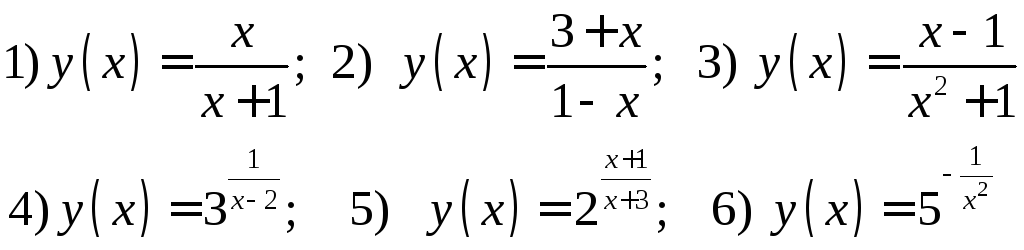
210. Исследовать данные функции на непрерывность и дать эскизы графиков
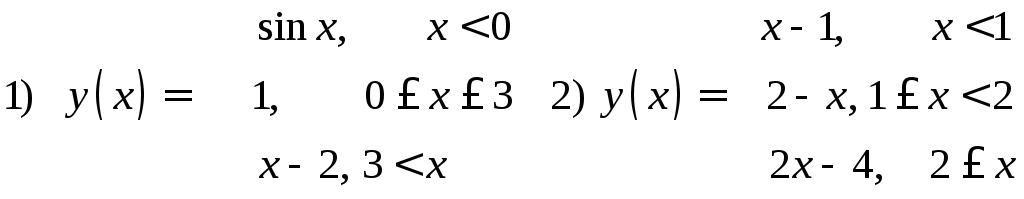
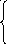

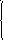
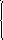

211. Среди данных интервалов ![]()
указать интервалы, в которых
функция
![]() достигает
своих
достигает
своих
наибольшего и наименьшего значений.
212. Доказать что данные функции непрерывны, дать эскизы графиков и по ним
найти наибольшее и наименьшее значения функций



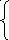


213. Исследовать данную
функцию![]() на непрерывность
на непрерывность
на множествах![]()
214. Доказать, что любой кубический многочлен имеет по крайней мере
один ноль.
