
- •Новосибирский государственный архитектурно- строительный
- •Определители
- •Матрицы.
- •Кривые в полярной системе координат.
- •Элементы векторной алгебры
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов.
- •Плоскости и прямые в пространстве
- •Введение в математический анализ
- •Предельные значения функции
- •Непрерывность и разрывы функций
- •Замечательные пределы
- •Дифференцирование функции от функции (Цепное правило).
- •Правило Лопиталя
- •Исследование функций и построение их графиков
- •Задачи на нахождение наибольших и наименьших значений функций
- •Кривизна дуги кривой.
- •93.1 93.2
- •173.1 173.2173.3 173.4
- •212.1 212.2
- •212.3212.4
- •220.1 220.2220.3220.4
- •294.1 294.2
Матрицы.
Укажите размерность матриц и определите, чему равны элементы
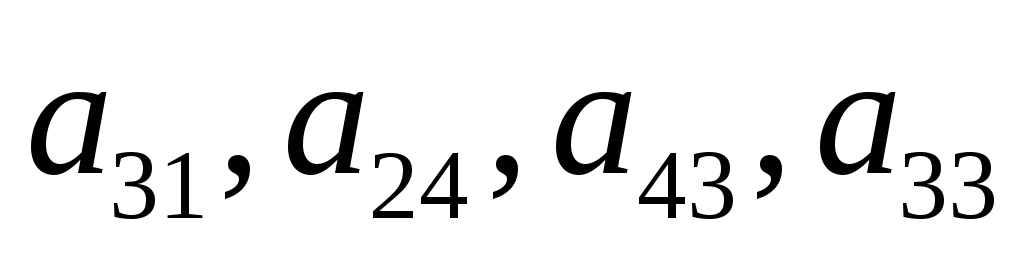
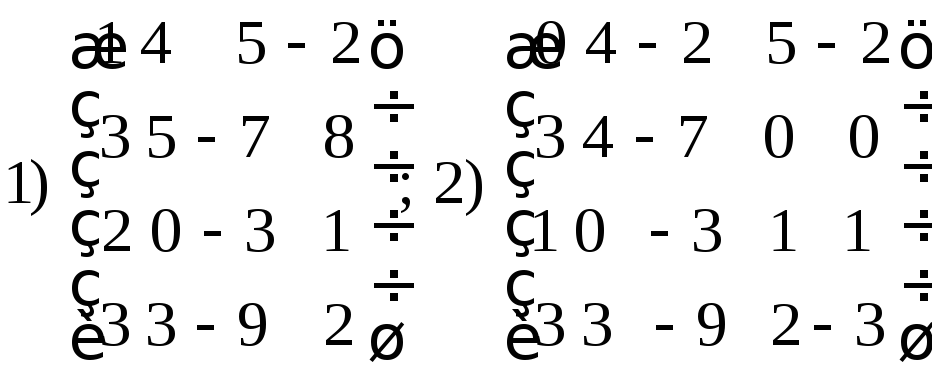
Определить параметры
 из
условий
из
условий
![]()
8. Можно ли вычислить линейную комбинацию
![]() .
Ответ поясните.
.
Ответ поясните.
9. Вычислить линейную комбинацию матриц
1)![]() ;
2)
;
2)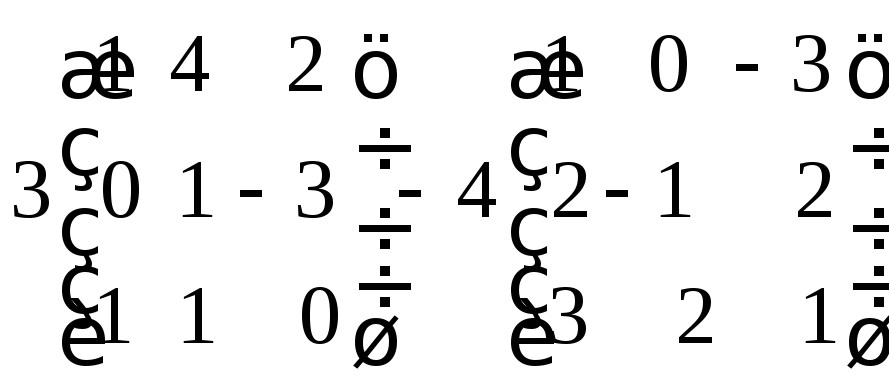 .
.
3)
 ;
4)
;
4) .
.
10. Вычислить линейную комбинацию
матриц
![]() ,
где Е- единичная матрица
,
где Е- единичная матрица
размером
![]() и
и

11. Решить уравнение
![]()
12. Вычислить произведение матриц
![]() ,
когда это возможно
,
когда это возможно
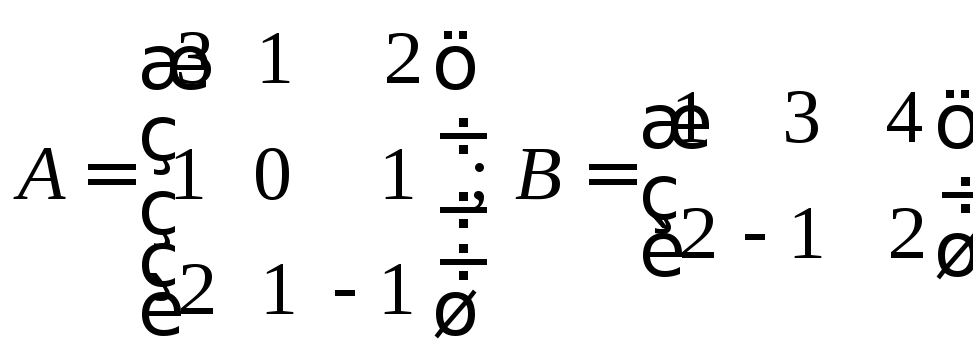
13. Вычислить произведения матриц

4)
![]() 5)
5)
6)
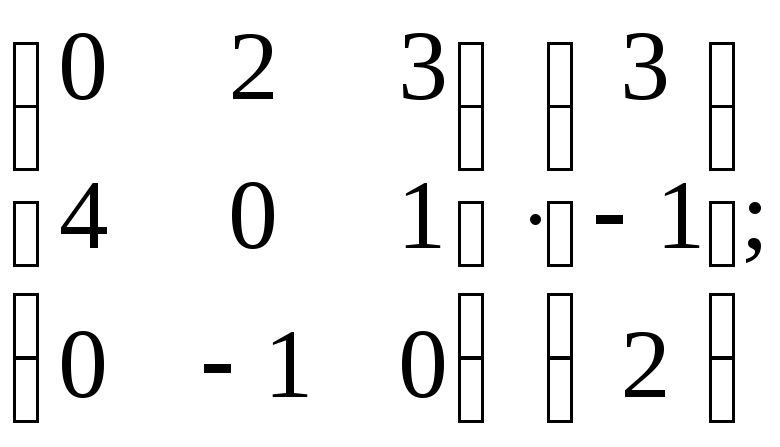 7)
7)
14.
Вычислить: ![]() ,
где
,
где
![]() единичная
матрица;
единичная
матрица; ![]()
15. Найти миноры всех элементов
матрицы ![]()

16. Определить максимальный и минимальный миноры элементов матриц
1)
![]() 2)
2)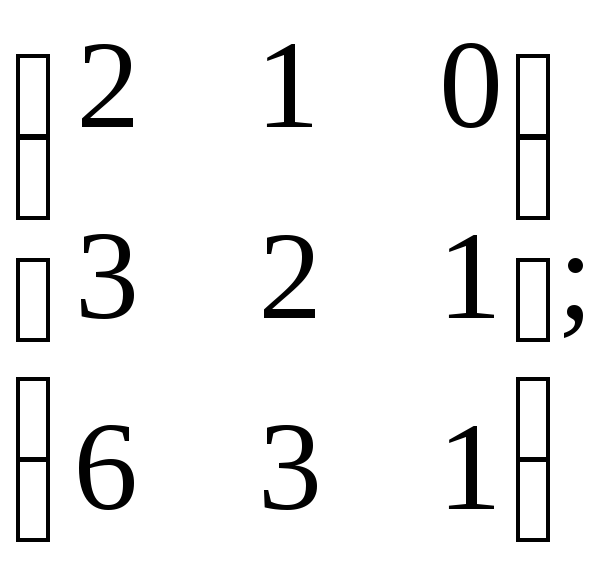 3)
3)
Проверить, что
 где матрицы
где матрицы и
и заданы
заданы
![]()
![]()
Пусть
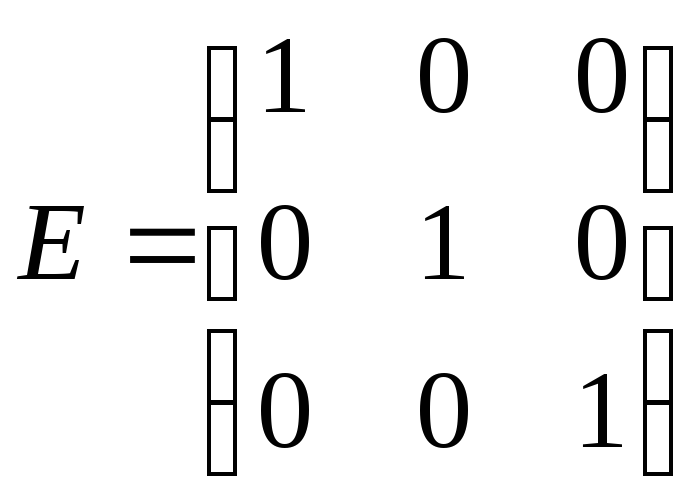 единичная матрица. Вычислить
единичная матрица. Вычислить
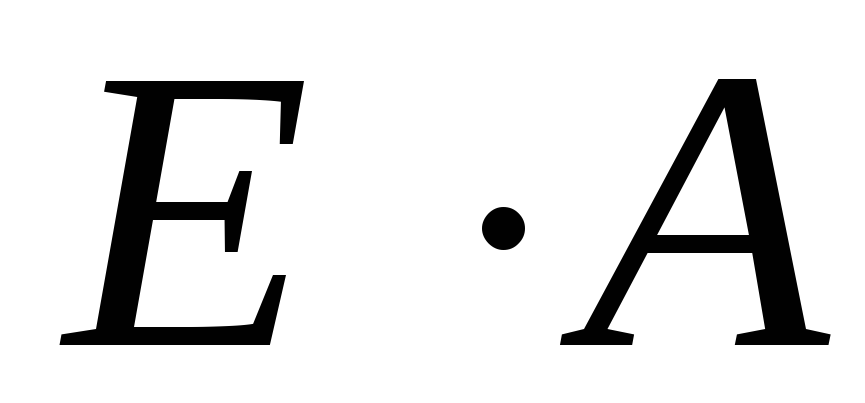 где
где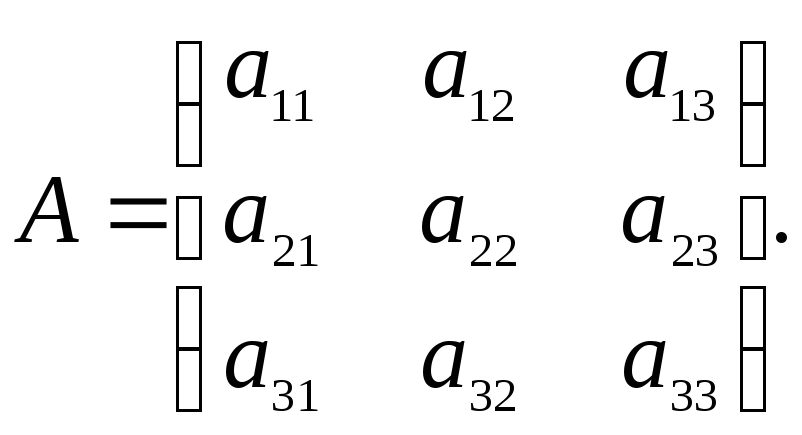
Найти ненулевую матрицу
 из
уравнения
из
уравнения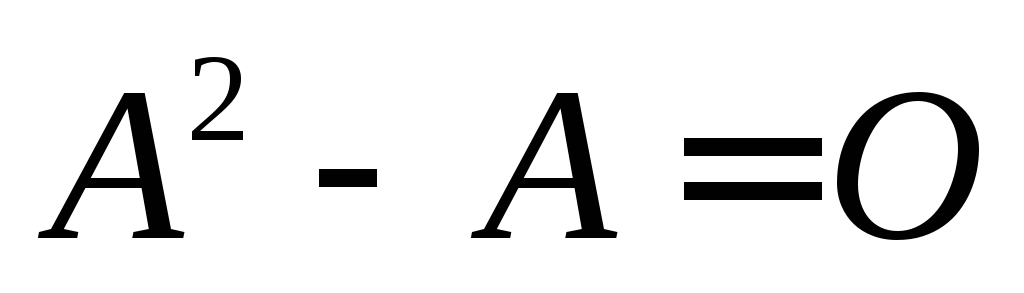 ,
где
,
где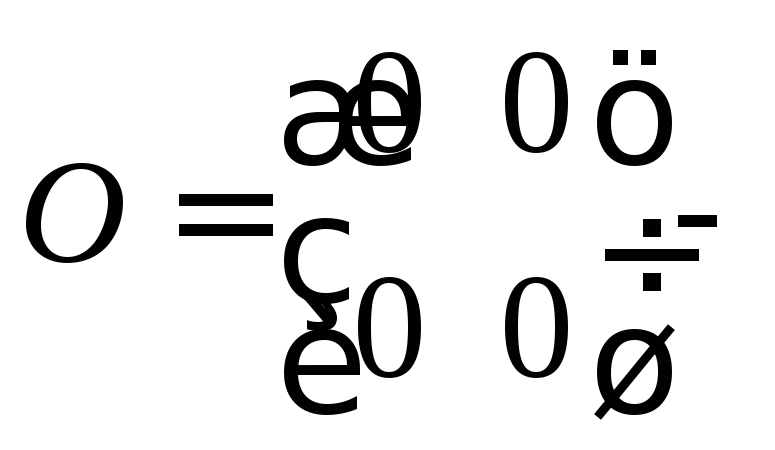 нулевая
матрица.
нулевая
матрица.Проверьте, являются ли матрицы
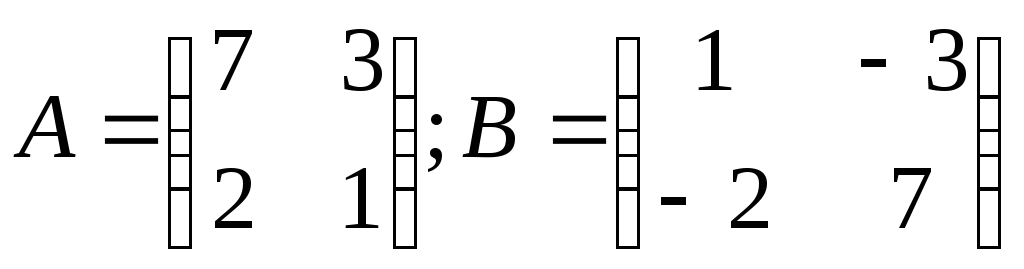 взаимно обратными?
взаимно обратными?Какая из двух матриц имеет обратную
 .
.
Ответ пояснить.
Вычислить матрицу
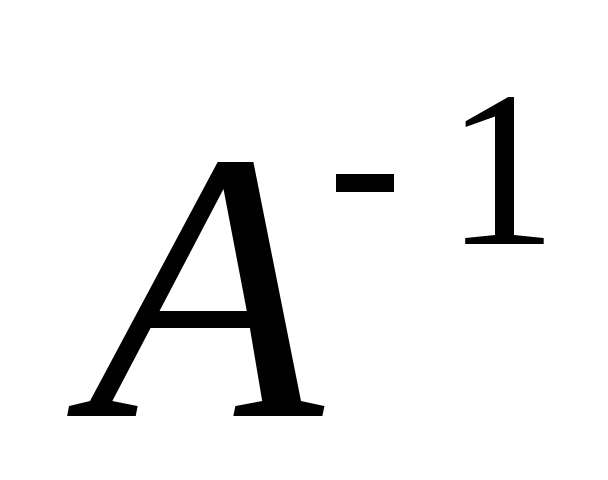 обратную
к данной матрице
обратную
к данной матрице
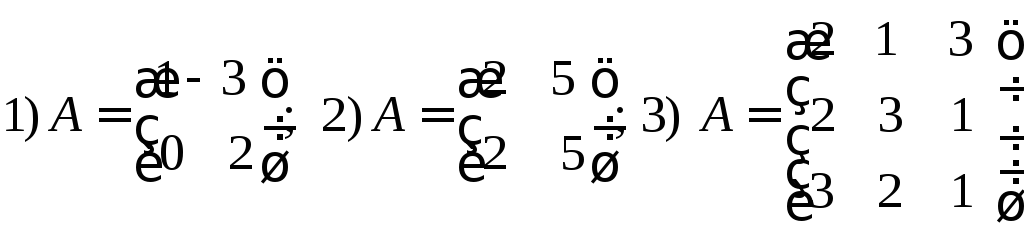 .
.
и сделать проверку полученного результата.
23. Используя элементарные преобразования , привести матрицу А к ступенчатому виду
 ;
;
24. Перемножить матрицы
![]()
25. Решить матричное уравнение![]() ,
где
,
где
![]()
Указание. Используйте обратную
матрицу![]() .
.
Системы линейных алгебраических уравнений
26. Проверить являются ли числа![]() решением данной системы
решением данной системы
линейных уравнений
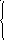
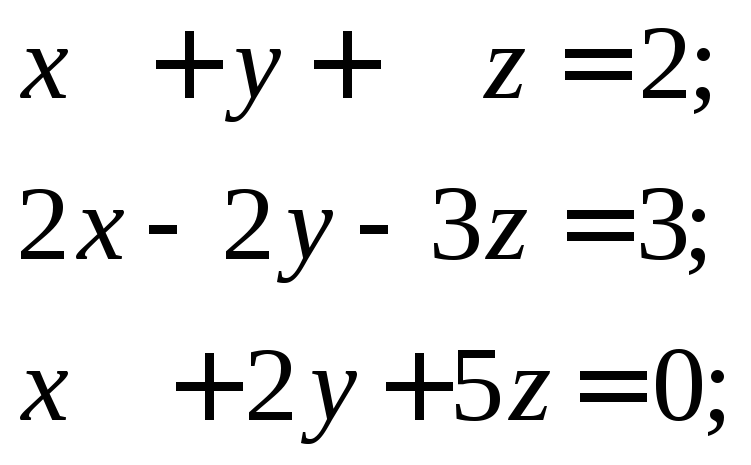
27. Проверить является ли
множество чисел![]() ,
зависящее от параметра
,
зависящее от параметра
t, решением данной системы линейных уравнений
![]()
28. К какой из данных систем можно применить метод Крамера
![]()
![]()
Определив эту систему, решите её.
29. Решить данные системы методом Крамера

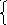

![]()
Сделать проверку полученных результатов.
30. Записать данные системы уравнений в матричном виде
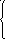
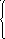
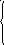
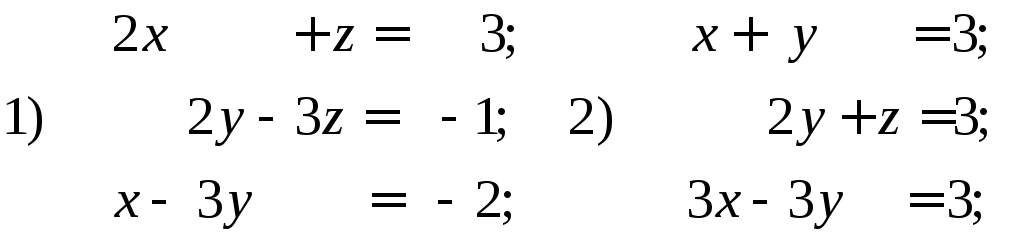
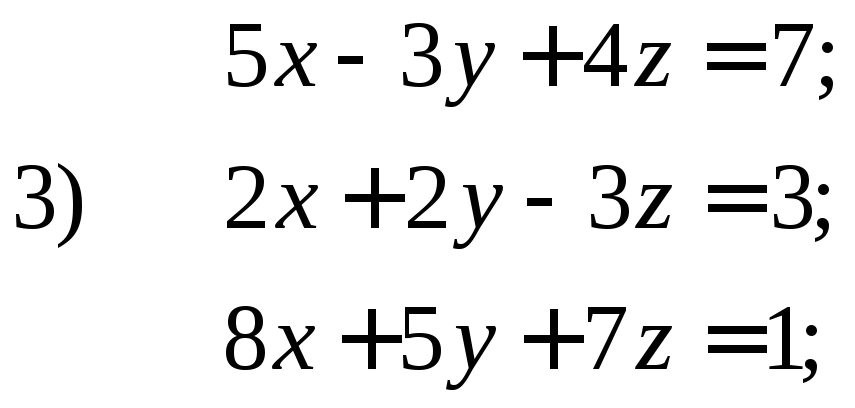
31. Решить системы матричным методом



![]()
![]()
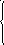
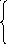
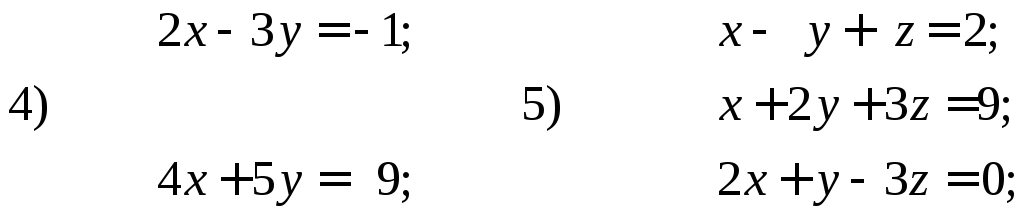
Сделать проверку полученных результатов. ![]()
32. Решить системы линейных алгебраических уравнений матричным методом и методом
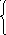
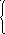 Крамера
Крамера
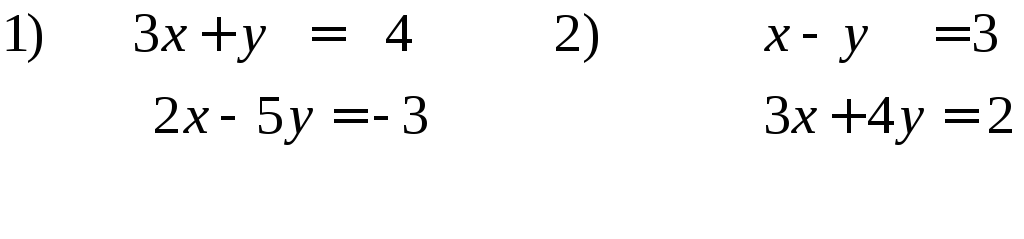
Если количество уравнений в системе не совпадает с числом неизвестных или определитель главной матрицы равен нулю, то решить такую систему методом Крамера или матричным методом невозможно. В этом случае система либо несовместна, ( не имеет решения), либо неопределенна ( имеет бесконечно много решений). Для решения таких систем используют метод Гаусса или его модификацию.
33. Решить систему линейных уравнений ступенчатого вида

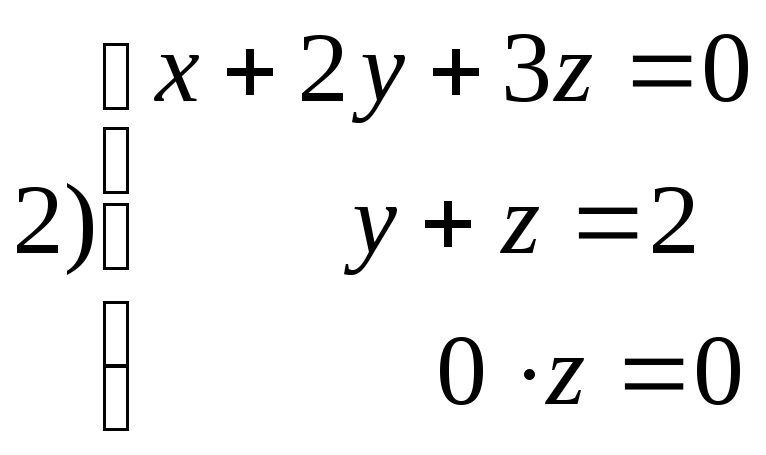

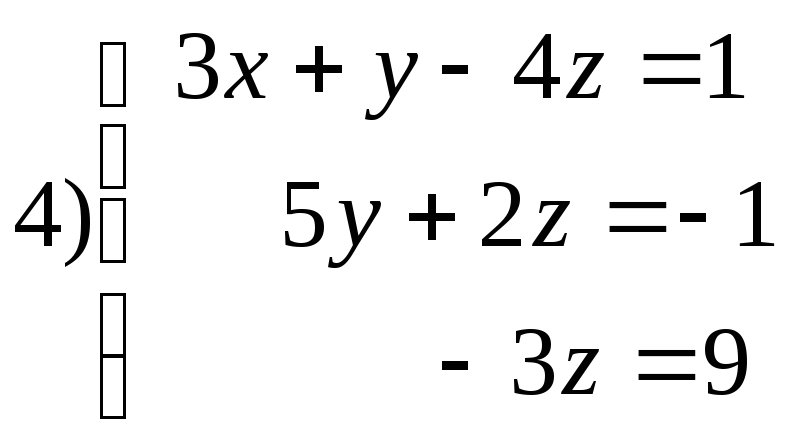
Метод Гаусса заключается в приведении системы линейных уравнений к ступенчатому виду и затем её решение.
Решение систем линейных алгебраических уравнений методом Гаусса.
 34. Для данных систем уравнений
34. Для данных систем уравнений


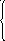
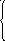

н аписать
расширенные матрицы.
аписать
расширенные матрицы.
35. По данным расширенным матрицам


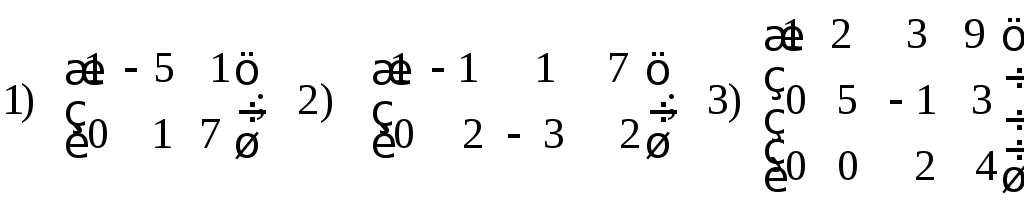

написать задающие их системы уравнений.
36. Проверить, что данные системы уравнений равносильны

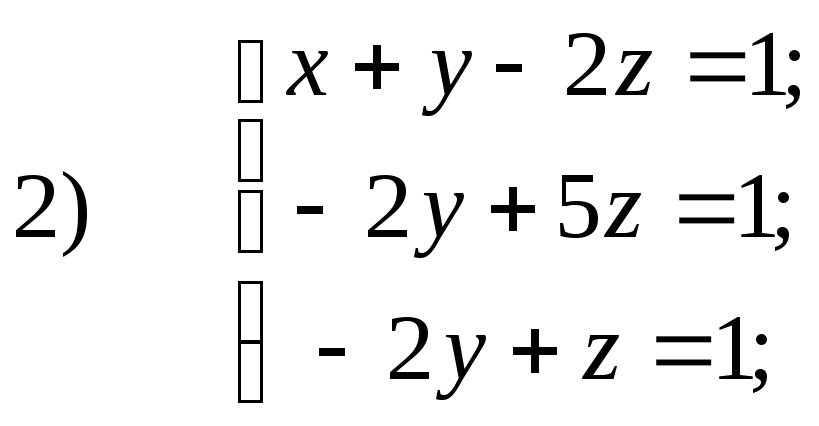
37. Решить данные системы уравнений методом Гаусса
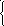
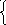
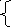
![]()
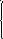
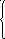 38. Решить
данные системы методом Гаусса
38. Решить
данные системы методом Гаусса
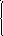 1)
1)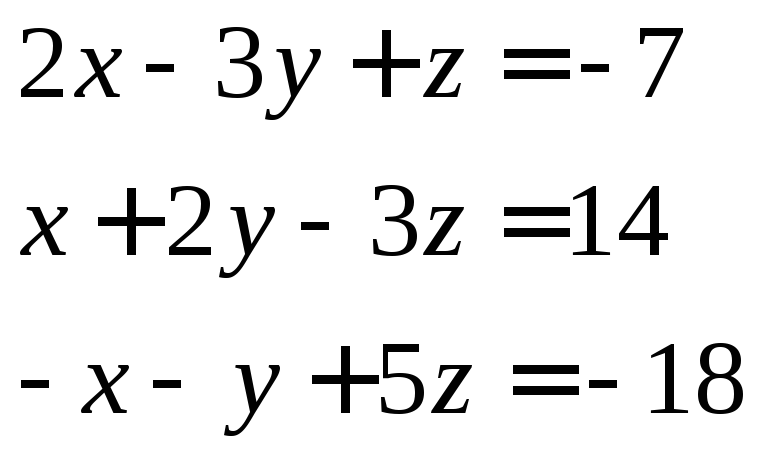 2)
2)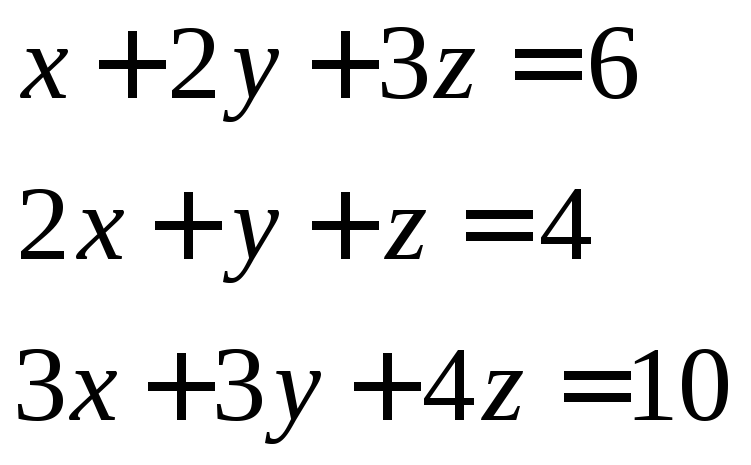

39. Решить данные системы методом Гаусса
1) ![]() 2)
2) ![]() 3)
3) 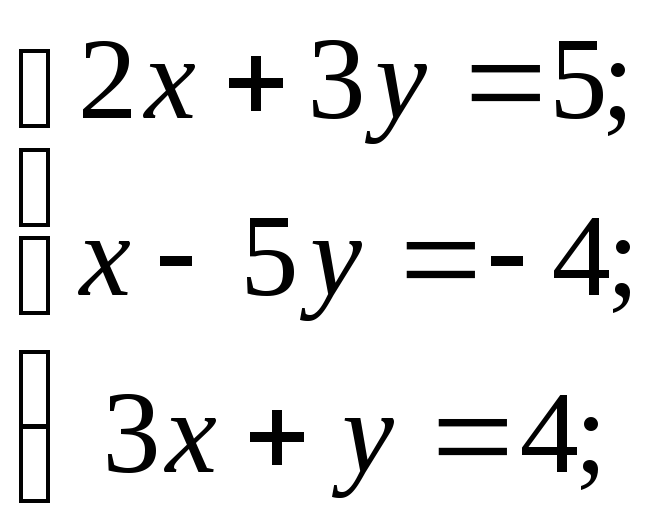
Элементы векторной алгебры и аналитической геометрии
Прямая линия на плоскости.
40.
Написать уравнение
горизонтальной прямой линии проходящей
через точку ![]() .
.
41.
Написать уравнение вертикальной прямой
проходящей через точку![]() .
.
Написать уравненияпрямой линии:
проходящей через точку
 и имеющей угловой коэффициент
и имеющей угловой коэффициент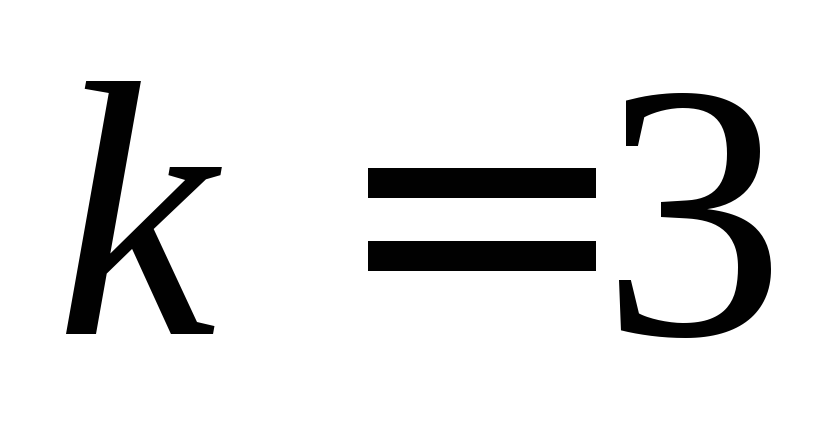 ;
;
2) проходящей через точку
![]() и
имеющей угловой коэффициент
и
имеющей угловой коэффициент ![]() ;
;
3) проходящей
через точку ![]() параллельно оси
ОХ;
параллельно оси
ОХ;
4) проходящей через точку
![]() параллельно оси
ОУ;
параллельно оси
ОУ;
5) проходящей
через точки ![]() ;
;
6) переписать уравнение прямой
линии![]() в общем виде;
в общем виде;
7) переписать
общее уравнение прямой линии
![]() в виде уравнения
в виде уравнения
с угловым коэффициентом.
На прямой линии
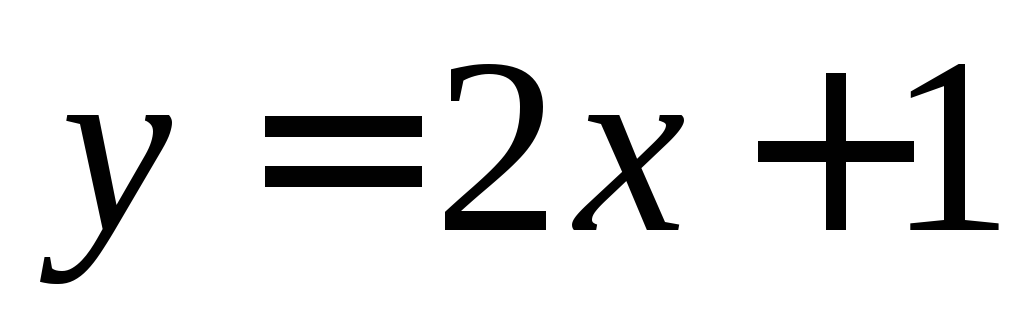 найти точки: 1) у которой абсцисса
найти точки: 1) у которой абсцисса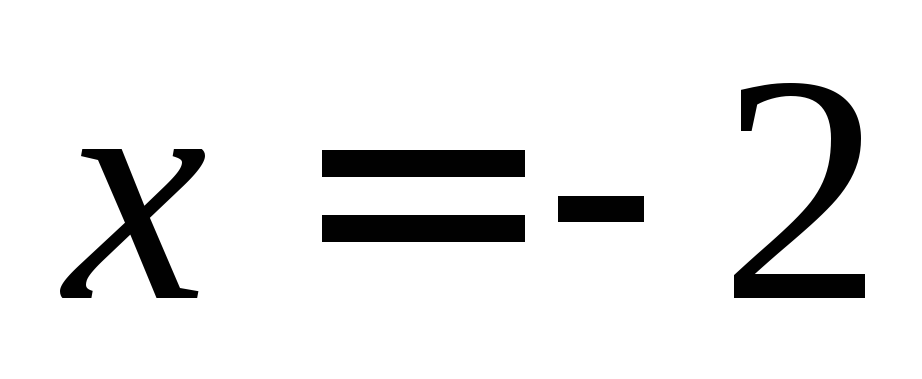 ;
2) у которой ордината
;
2) у которой ордината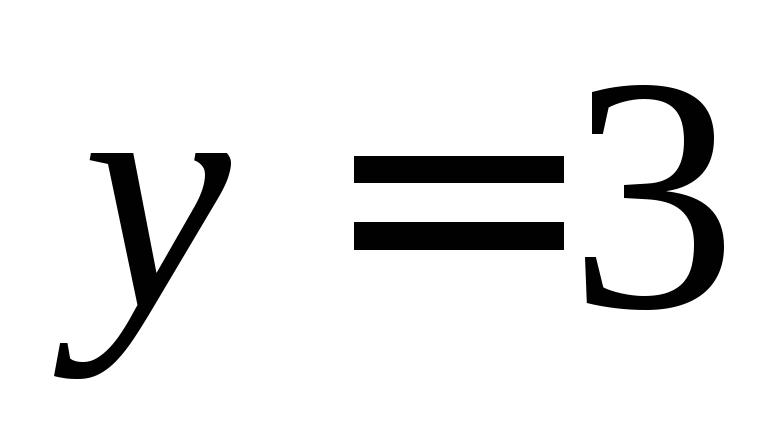 ;
3) Лежат ли точки
;
3) Лежат ли точки на
прямой
на
прямой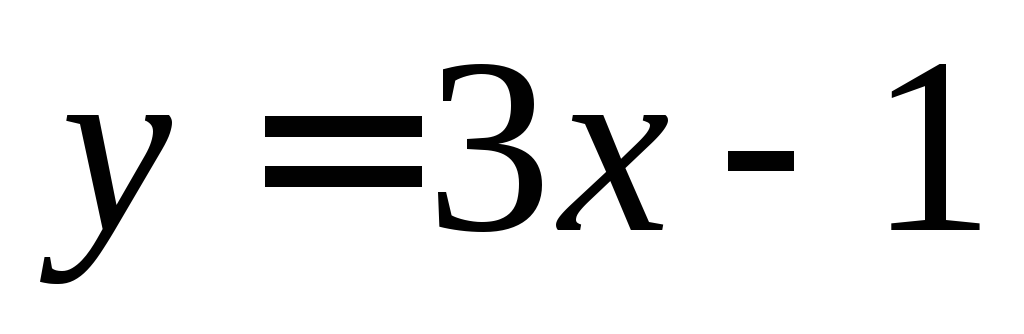 .
.Написать уравнение прямой линии проходящей через точку
 параллельно
прямой линии
параллельно
прямой линии
1)
![]() 2)
2)![]() 3)
3)
![]() 4)
4)![]()
Написать уравнение прямой линии проходящей через точку
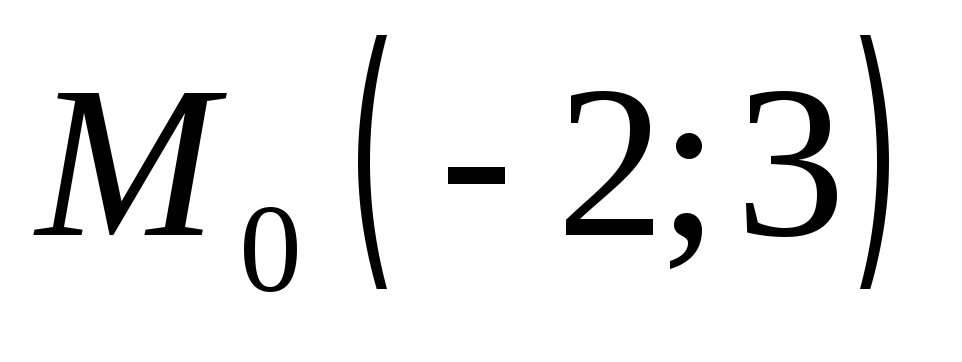 и
и
перпендикулярно прямой линии:
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
Нарисовать эскизы графиков прямых
![]()
Используя калькулятор вычислить угол наклона прямых линий
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
Найти точки пересечения прямой линии
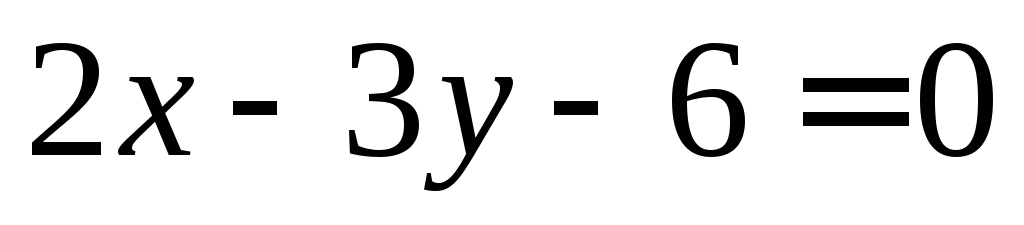 с осями ОХ, ОУ.
с осями ОХ, ОУ.Найти точки пересечения прямых линий. Сделать чертёж.
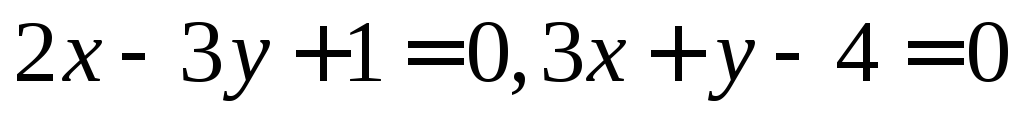 ;
; ,
, ;
;
3)
![]()
4)
![]()
![]()
Найти координаты вершин треугольника
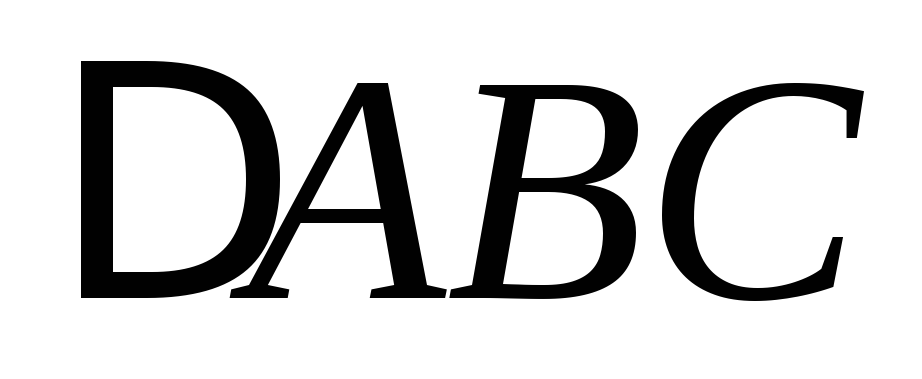 со сторонами определяемыми
уравнениями
со сторонами определяемыми
уравнениями
![]()
![]()
![]()
![]()
![]()
![]()
Найти уравнения прямых, на которых лежат стороны
 ,
имеющего вершины
,
имеющего вершины
![]() .
.
Найти острый угол между прямыми линиями:
![]()
Определить какие из точек

лежат выше прямой, на прямой и ниже
прямой, проходящей через точки
![]() .
.
Даны уравнения сторон четырёхугольника
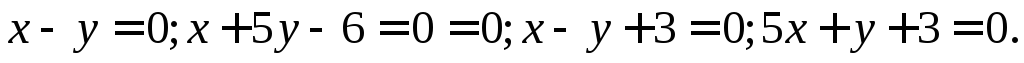 Найти
уравнения его диагоналей.
Найти
уравнения его диагоналей.Найти абсциссу
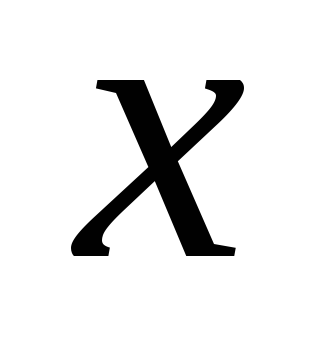 ,
чтобы четырёхугольник с вершинами
,
чтобы четырёхугольник с вершинами
 был
параллелограммом.
был
параллелограммом.Доказать, что диагонали четырёхугольника с вершинами
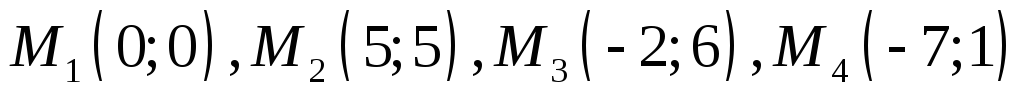 взаимно перпендикулярны.
взаимно перпендикулярны.Используя калькулятор вычислить расстояние от начала координат до прямой
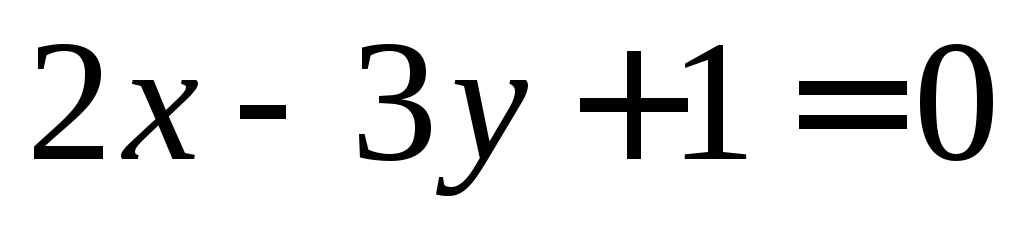 .
.Используя калькулятор вычислить расстояние от точки
 до прямой
до прямой 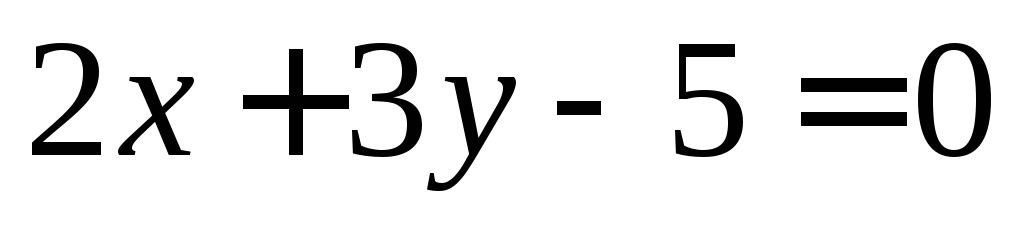 .
.Даны вершины
 :
: .Найти
: 1) уравнение стороны
.Найти
: 1) уравнение стороны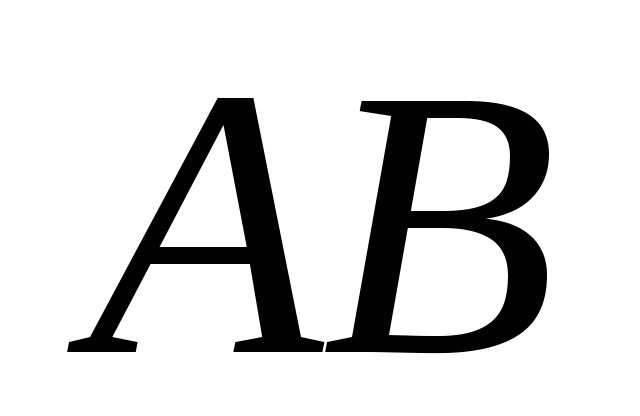 ;
2) уравнение высоты
;
2) уравнение высоты ;
3) уравнение медианы
;
3) уравнение медианы ;
4)точку пересечения высоты
;
4)точку пересечения высоты и
медианы
и
медианы ;
5) уравнение прямой, проходящей через
вершину
;
5) уравнение прямой, проходящей через
вершину параллельно стороне
параллельно стороне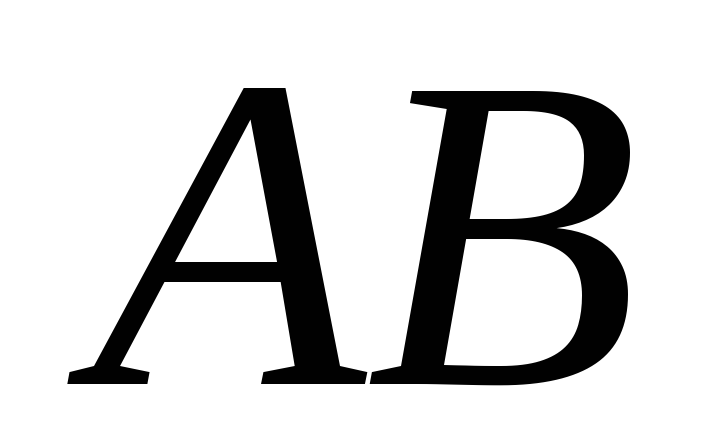 ;
6) длину высоты
;
6) длину высоты ;
7) величины углов
;
7) величины углов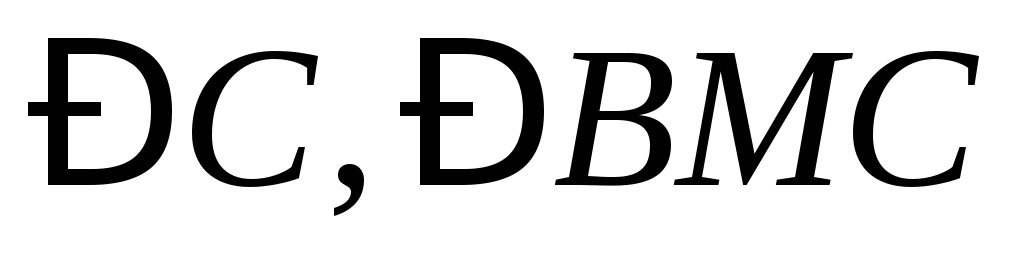 .
.Найти точку
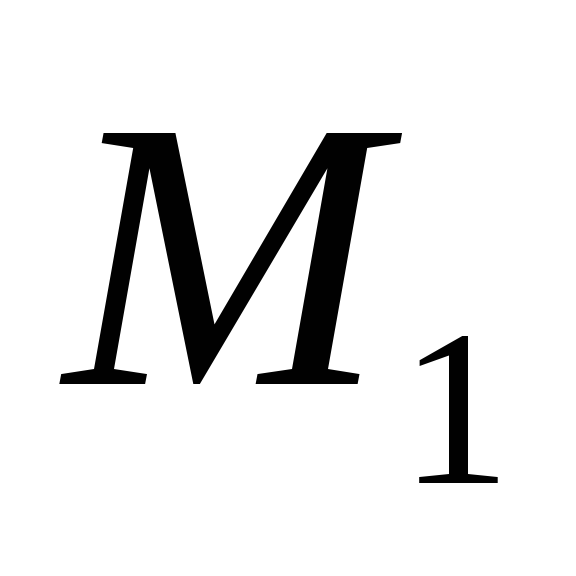 симметричную
точке
симметричную
точке относительно
прямой
относительно
прямой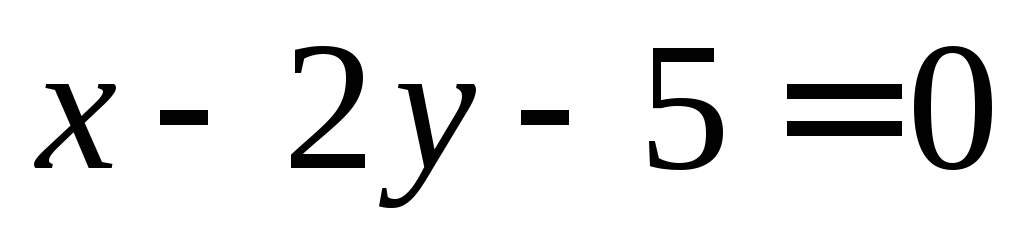 .
.
Кривые второго порядка
Парабола.
Написать уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси ОХ и её параметр равен 3.
Определить величину параметра и дать эскизы парабол
![]()
Определить величину параметра, фокус, директрису и дать эскиз.
1)
![]() 2)
2)![]() 3)
3)![]() 4)
4)![]()
Написать уравнение параболы, которая имеет фокус
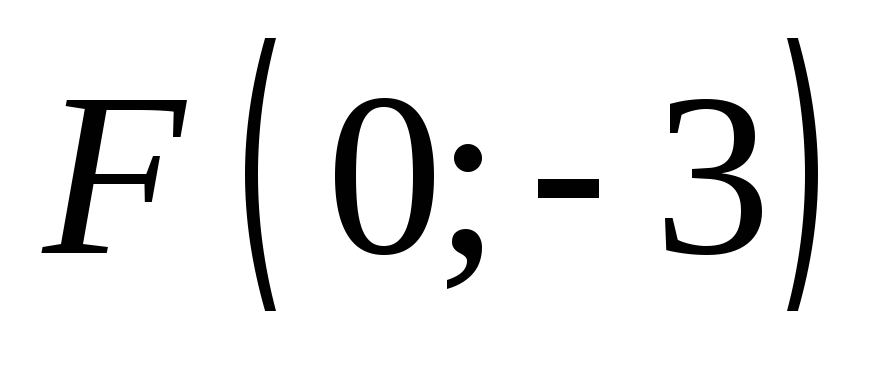 и
вершину в начале координат.
и
вершину в начале координат.
Написать уравнение параболы, которая имеет фокус
 и
вершину в начале координат.
и
вершину в начале координат.Написать уравнение параболы, у которой фокус
 и
уравнение директрисы
и
уравнение директрисы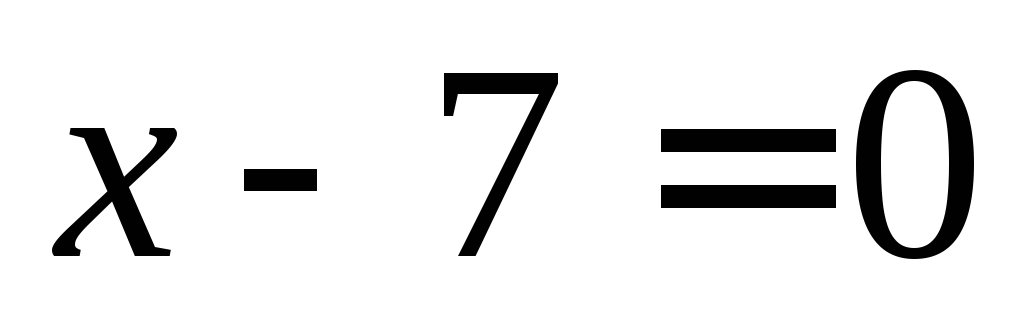 .
.Написать уравнение параболы с вершиной
 и осью симметрии
и осью симметрии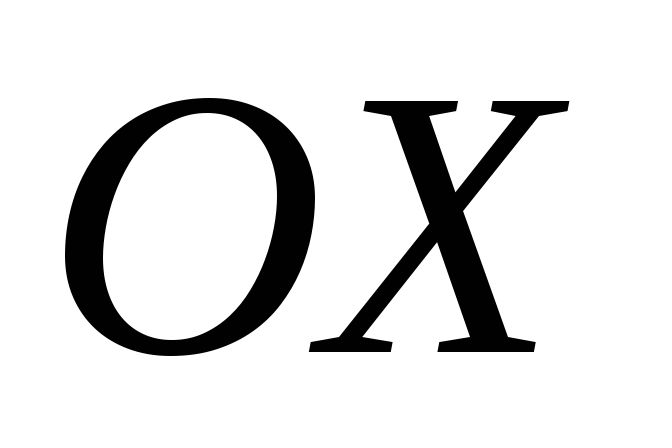 .
Парабола проходит через точку
.
Парабола проходит через точку
1) ![]() ;
2)
;
2)![]() .
.
Написать уравнение параболы с вершиной
 и осью симметрии
и осью симметрии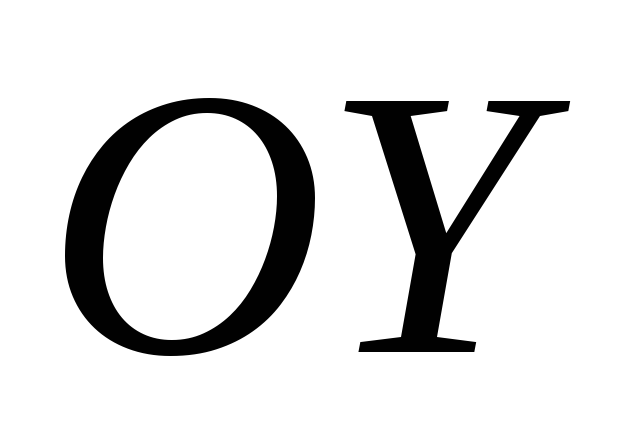 .
Парабола проходит через точку
.
Парабола проходит через точку
1) ![]() ;
2)
;
2)![]() .
.
69. Найти точки пересечения прямой и параболы:
1)
![]()
![]() 2)
2)![]()
![]()
Окружность
70. Написать уравнение окружности, зная
её центр О
 и
радиус
и
радиус ;
2) её центр О
;
2) её центр О и
радиус
и
радиус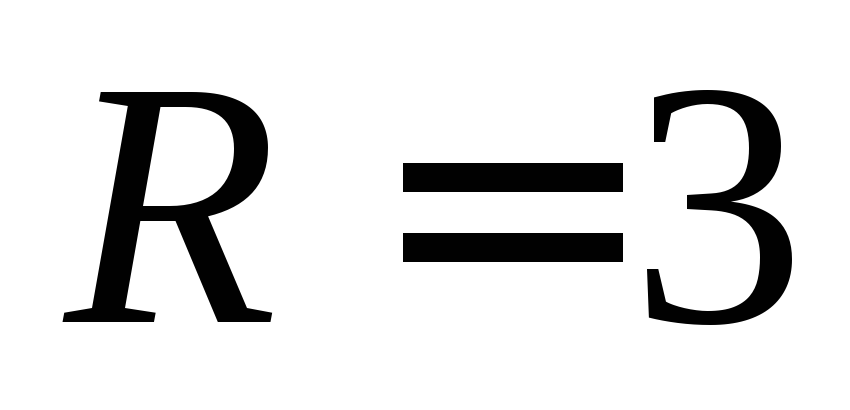 ;
;
71. Найти точки пересечения окружности
![]() с
осями координат.
с
осями координат.
Эллипс.
72. Написать каноническое уравнение эллипса, фокусы которого лежат на оси
абсцисс симметрично относительно начала координат, зная, что
его полуоси равны 3 и 4;
его большая полуось равна 10, а расстояние между фокусами 2с=12;
расстояние между его фокусами 2с=8, а эксцентриситет
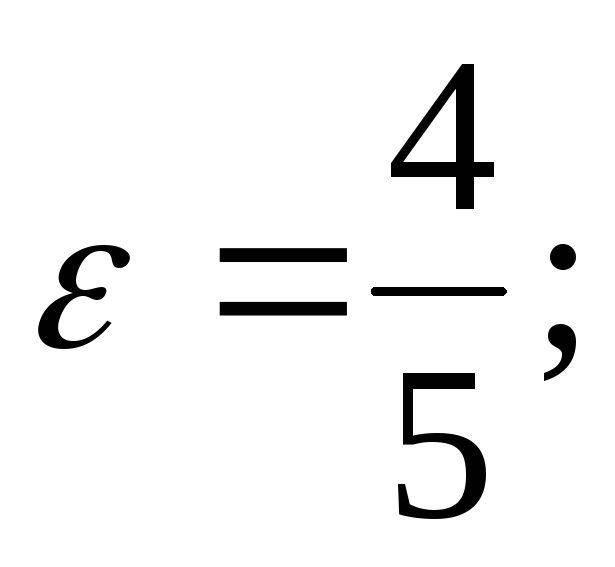
расстояние между его директрисами равно
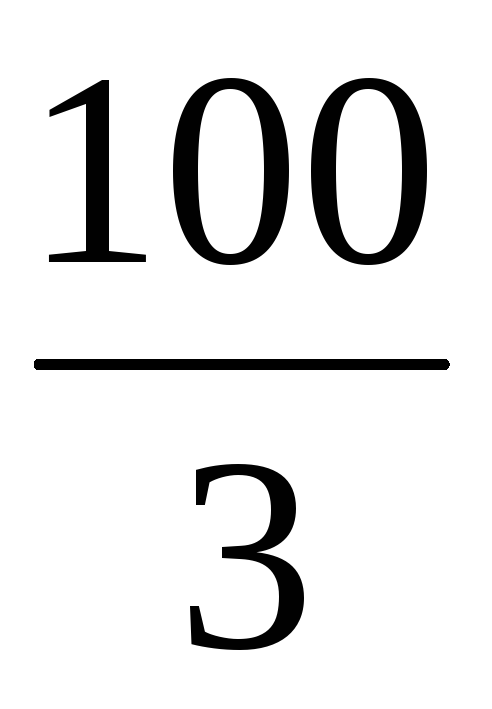 и расстояние между
и расстояние между
фокусами 2с=12.
Пункты 2 и 4 снабдить подробным чертежём.
73. Написать каноническое уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, что (пункты 2,4 и 6 снабдить подробным чертежем )
1) его полуоси равны 3 и 4;
его большая полуось равна 10, а расстояние между фокусами 2с=16;
расстояние между его фокусами 2с=12, а эксцентриситет
 ;
;расстояние между его директрисами равно
 и расстояние между
и расстояние между
фокусами 2с=12;
Пункты 2 и4 снабдить подробным чертежём.
74. Дан эллипс![]() .
Найти его
.
Найти его
полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
Дать эскиз.
75. Дать эскиз графика кривой и указать, что это за кривая
1)![]() 2)
2)![]() .
.
76. Ординату каждой точки окружности с центром в начале координат и радиусом равным 1.
уменьшили в 3 раза. Назвать полученную кривую, определить её параметры и сделать
эскиз её графика.
77. Абсциссу каждой точки окружности с центром в начале координат и радиусом равным 1.
уменьшили в 2 раза. Назвать полученную кривую, определить её параметры и сделать
эскиз её графика.
78.
Даны фокусы эллипса ![]() .
Написать уравнения осей его симметрии.
.
Написать уравнения осей его симметрии.
79.
Даны: уравнение директрисы параболы
![]() и её фокус
и её фокус ![]() .
Написать уравнение
.
Написать уравнение
оси симметрии параболы.
Гипербола.
80. Написать уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что
её полуоси
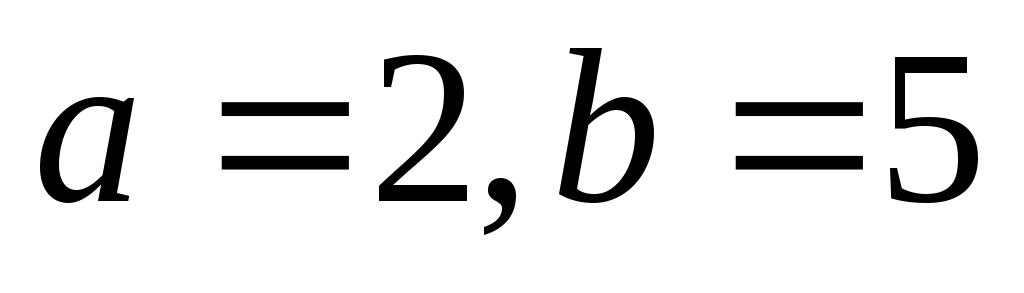 ;
;её горизонтальная ось 8 , а расстояние между фокусами
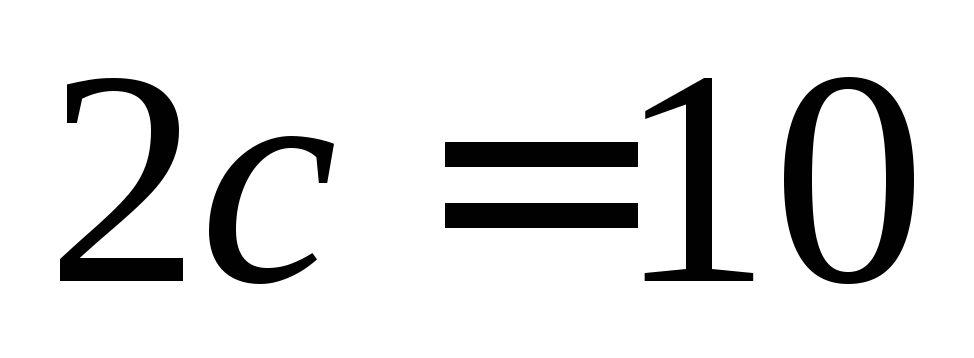 ;
;расстояние между её фокусами 2с=10, а эксцентриситет
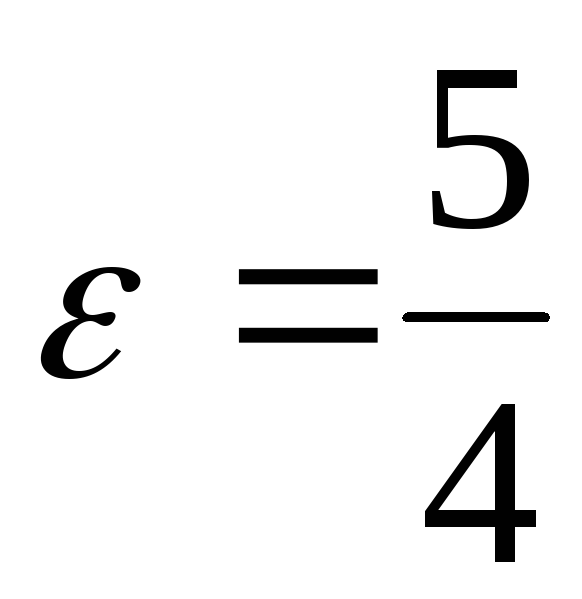
 ;
;расстояние между её директрисами равно
 и расстояние между
и расстояние между
фокусами 2с=20;
Пункты 2 и 4 снабдить подробным чертежем.
81. Написать уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, что
её полуоси равны
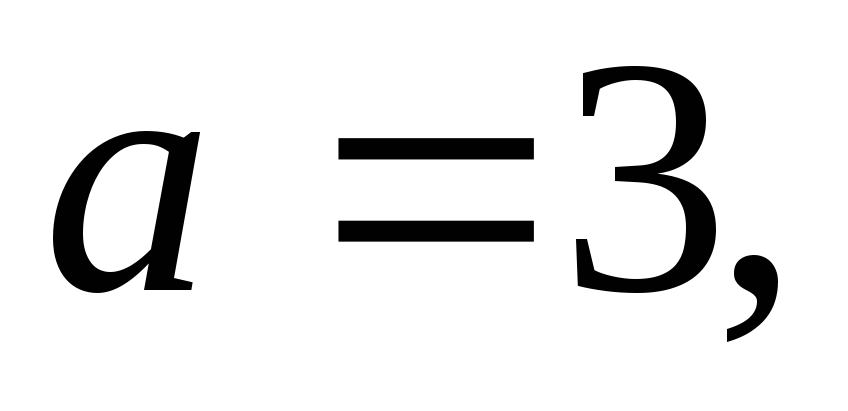

её горизонтальная полуось равна 3, а расстояние между фокусами
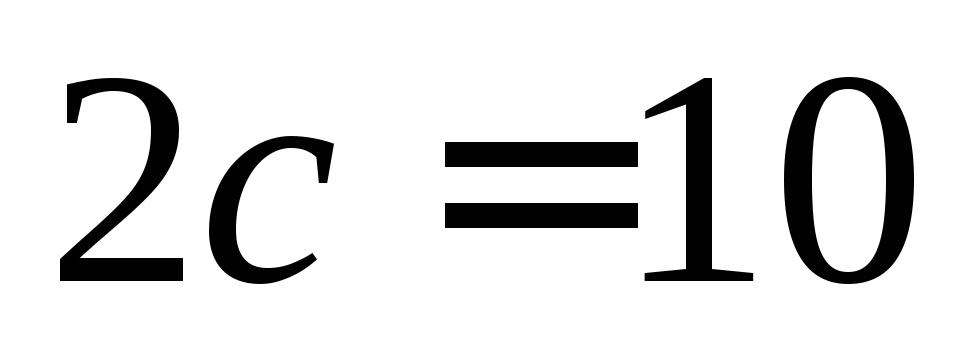 ;
;расстояние между её фокусами 2с=20, а эксцентриситет
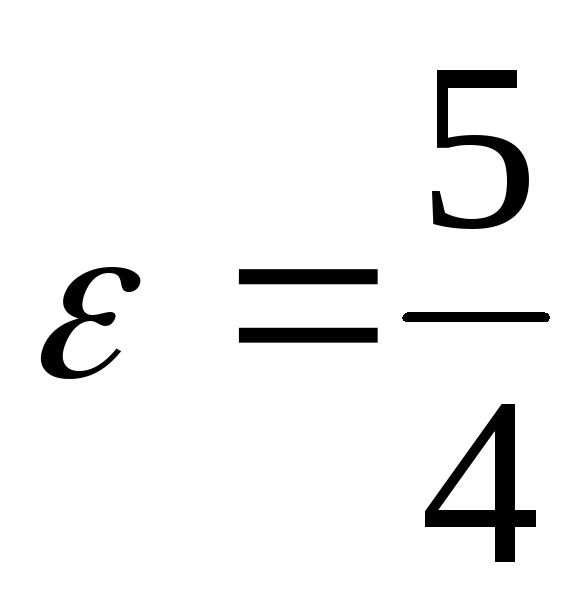 ;
;расстояние между её директрисами равно
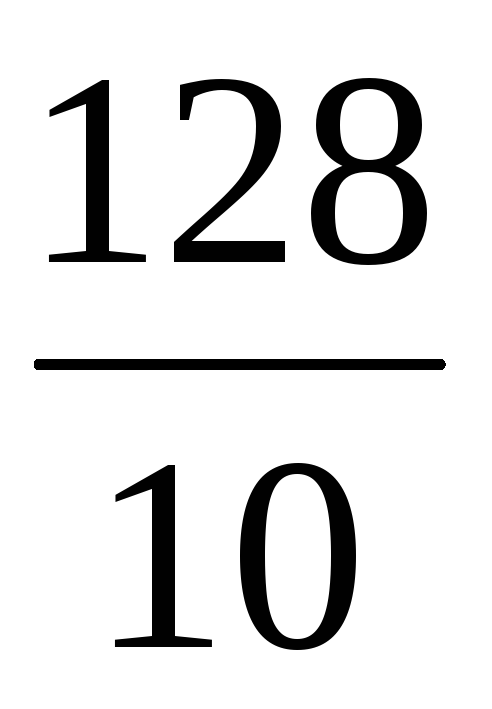 и расстояние между
и расстояние между
фокусами 2с=20;
Пункты 2 и 4 снабдить подробным чертежем.
82. Определить, на какой из координатных осей лежат фокусы данных кривых второго
порядка
![]()
83. Дано уравнение гиперболы
![]() .
Найти её
.
Найти её
полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис; 5) уравнение асимптот.
Построить чертеж гиперболы.
84. Пусть задано уравнение кривой второго
порядка:
![]() .
.
Определить:
1) название кривой; 2) полуоси кривой; 3) координаты фокуса(ов) и их расположение;
4) эксцентриситет кривой; 5) уравнение директрисы(с) кривой.
Если у кривой есть асимптоты, то написать их уравнения. Построить чертеж кривой.
85. Пусть задано уравнение кривой второго
порядка:![]() .
Определить:
.
Определить:
1) название кривой; 2) полуоси кривой; 3) координаты фокуса(ов) и их расположение;
4) эксцентриситет кривой; 5) уравнение директрисы(с) кривой.
Если у кривой есть асимптоты, то написать их уравнения. Построить чертеж кривой.
86. Пусть задано уравнение кривой второго
порядка:![]() .
Определить:
.
Определить:
1) название кривой; 2) полуоси кривой; 3) координаты фокуса(ов) и их расположение;
4) эксцентриситет кривой; 5) уравнение директрисы(с) кривой.
Если у кривой есть асимптоты, то написать их уравнения. Построить чертеж кривой.
87. Определить тип кривой и построить
чертеж кривой:
![]()
88. Определить тип кривой и построить
чертеж кривой:![]()
