220.1 220.2220.3220.4

221. 1) уравнение касательной: уравнение нормали: точки пересечения касательной с осями координат:

2) уравнение касательной: уравнение нормали: точки пересечения касательной с осями координат:

3) уравнение касательной: уравнение нормали: точки пересечения касательной с осями координат:

222.

223.1

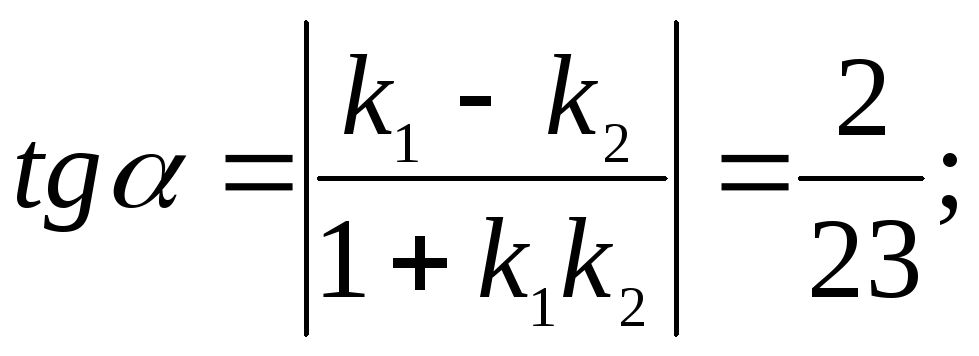
223.2

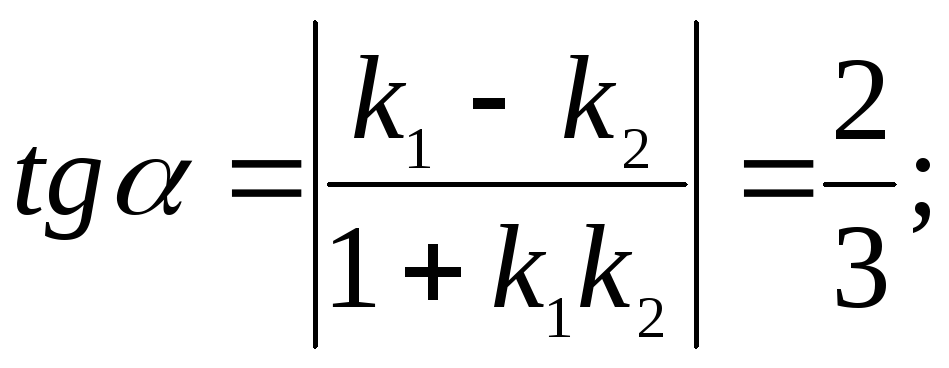
223.3

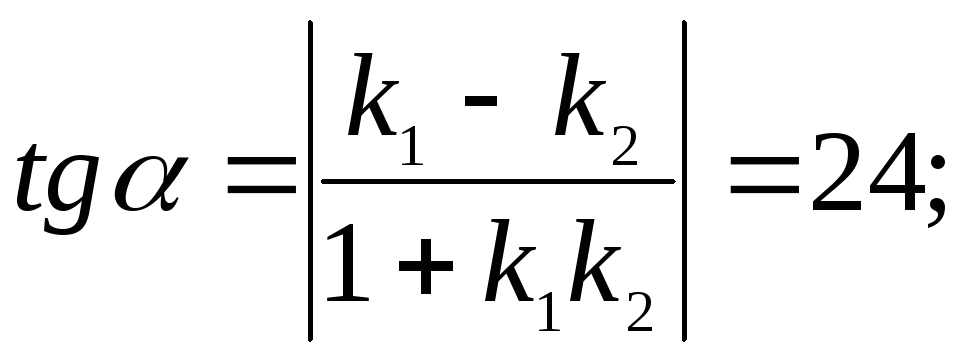
224.

225. 1) Графики функций ипересекаются в двух точках с абсциссами и х=3.

Острый угол между графиками этих функций в точке равен в точке угол равен .

2) Графики функций ипересекаются в точке с абсциссой 0 под углом

3) Графики функций ипересекаются в точке с абсциссой 1 под углом

226.

226.1 226.2

227.1 227.2

227.3 227.4

228. Скорости совпадают т.е. при

229.1 229.2229.3229.4

229.5 229.6229.7

229.8 229.9229.10

230.1 230.2

230.3 230.4

230.5 230.6230.7

230.8. 230.9

230.10 230.11230.12

230.13 230.14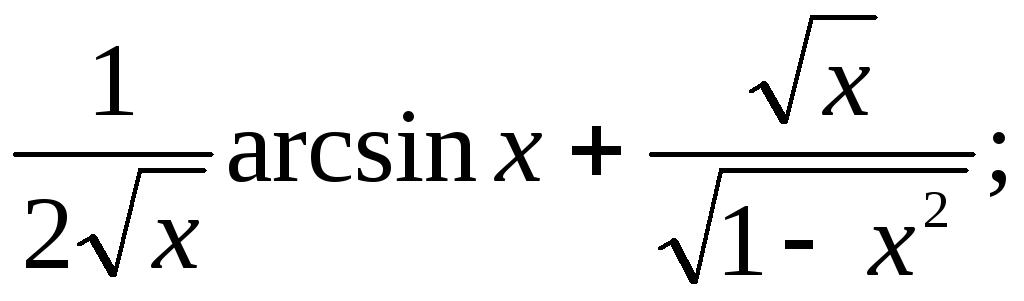230.15

231.1 231.2231.3231.4

231.5 231.6231.7231.8

232.

233. 1 233.2

233.3 233.4

233.5 233.6

233.7

233.8 233.9

234. Вычислим и вместе с подставим в данное уравнение.

234.1 ;

234.2

234.3

235.1 235.2235.3

235.4 235.5

236. Вычислим и вместе с подставим в данное уравнение.

Дифференцирование функции от функции.

237.1 237.2237.3237.4

237.5 237.6

237.7 237.8237.9

237.10 237.11

237.12 237.13237.14237.15

237.16 237.17237.18

237.19 237.20237.21

237.22 237.23

237.24 237.25237.26

237.27 238.1 238.2238.3

239. 1) 2)3)поясните результат.

240. 1) Рассмотрим функцию обратная к ней: . Пользуясь теоремой о производной обратной функции, имеем:

2) Рассмотрим функцию обратная к ней: . Пользуясь теоремой о производной обратной функции, имеем:

Логарифмическое дифференцирование.

241.1

241.2

241.3

241.4

Формулы неявного дифференцирования.

242. 1) Преобразуем параметрическую форму записи, исключив Для этого возведем в квадрат и , разделим первое уравнение на 4, а второе на 9 и сложим их:

2)

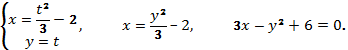
3)

243.1 243.2243.3

243.4 243.5243.6243.7

243.8 243.9

244.1

244.2

_{Формулы параметрического дифференцирования.}

245.

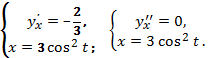
246.1 246.2

246.3 246.4.

247.1

Угловой коэффициент равен нулю, значит, уравнение касательной имеет вид: а нормали

247.2 247.3

247.4

248.1

248.2

_{Дифференциал функции.}

249.1 249.2249.3

249.4 249.5249.6

249.7 249.8249.9

249.10 249.11

249.12

251.1 251.2

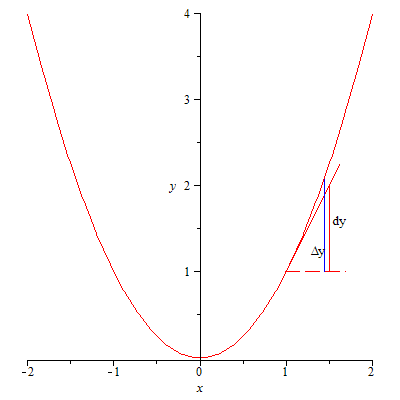
251.3 251.4

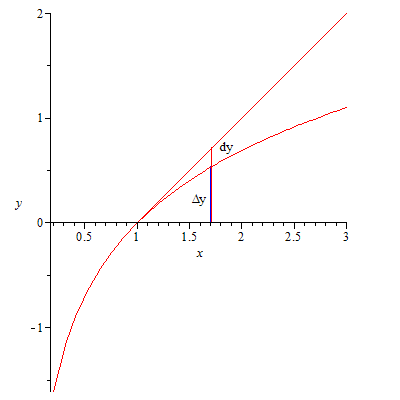
252.1

252.2 ;

252.3

252.4

252.5

253.

254.

255.1

255.2

255.3

255.4

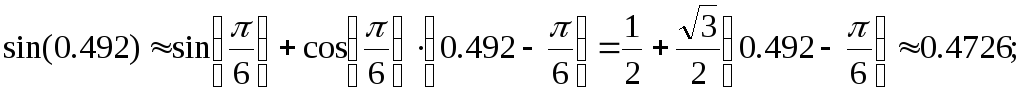
256.1 . 256.2.

257.

258. .

259.1 Существует число такое чтоНайдем это число.

259.2

259.3

_{Правило Лопиталя.}

260. 1 По правилу Лопиталя

260.2 260.3260.4

260.5 260.6260.70; 260.8 0.5; 260.9 1.

261. 1) 0;

262. 1) Прямая является горизонтальной асимптотой, если .

горизонтальная асимптота.

263. 1) Если предел , то прямая является вертикальной асимптотой. вертикальная асимптота.

горизонтальная асимптота.

вертикальная асимптота, горизонтальная асимптота.

вертикальная асимптота, горизонтальная асимптота.

Приложение дифференцирования к задачам геометрии и механики.

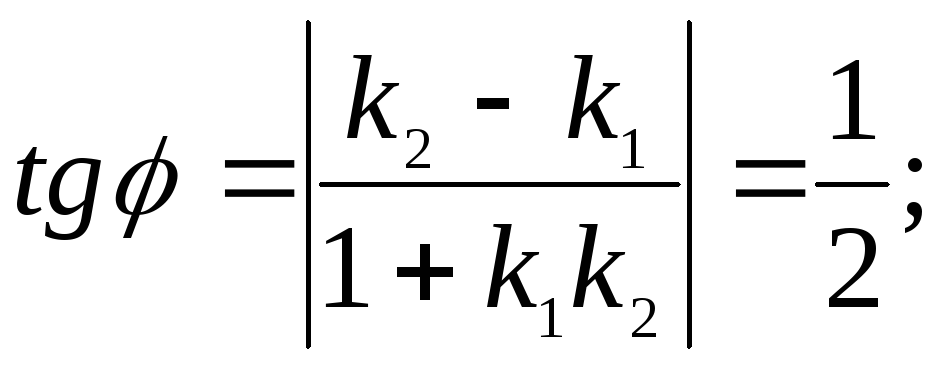
264. 265.

266. 267.. 268.

269. . 270. 271.1 в точке (0;0),

в точке 271.2 в точке (0;0), в точке

272. 273.убывает. 274. возрастает.

275.1 275.2 275.3

276.1 276.2 276.3

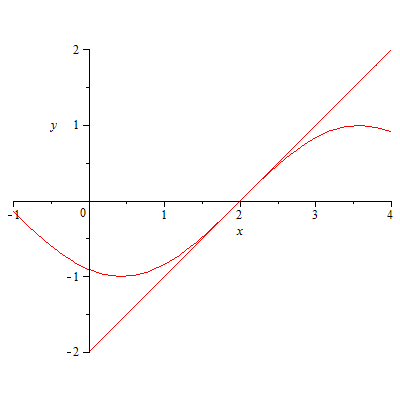
276.4 277

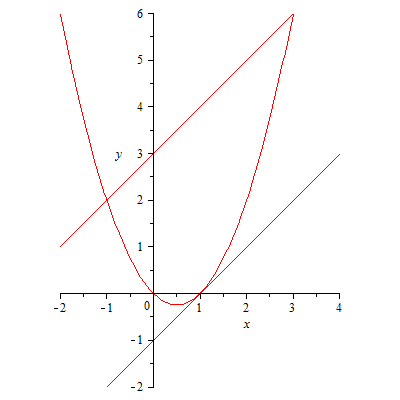М(3;6).

278. 279.1

280. 281.1281.2

281.3

Исследование функций и построение их графиков.

282.1 возрастает на интервалах , убывает на282.2 убывает на интервалах возрастает на

282.3 убывает на интервалах возрастает на

282.4 возрастает на интервалах убывает на

282.5 возрастает на интервалах убывает на

282.6 возрастает на интервалах убывает на

283.1 возрастает на интервале убывает на

283.2 убывает на интервалах возрастает на

283.3 убывает на интервалах возрастает на

283.4 возрастает на интервале , убывает на

283.5 возрастает на интервале , убывает на

283.6 возрастает на интервале , убывает на

284.1 min (2;-1); 284.2 max(1;-4); 284.3 min (0;0); max(1;1); 284.4 min (-1;3);

min (4;-128); max(0;0); 284.5 max (1;0); min (5/3;44/3); 284.6 min(--64);

min(-64); max (0;0).

285. ; на (-ина (5;

286. на (и на (10;.

287.1 min (-1;-1/e); 287.2 min (0;0), max (-2;4/e²); 287.3 min (0;0); 287.4 max(0;1);

287.5 min (-1;-1/2), max (1;1/2); 287.6 min(1/e; -1/e); 287.7 min(1/

287.8 min (1;0), max (e^-2;4/e²). 288. Т.е доказать, что выпукла вниз, т.е.

ч.т.д.

289.1 точка перегиба (1;0), выпукл вверх на (-выпукл вниз на (1;);

289.2 точка перегиба (3;-648), выпукл вниз на (3;выпукл вверх на (-;0),(0;3);

289.3 точка перегиба (1/3;-119/27), выпукл вверх на (-выпукл вниз на (1/3;).

290.1 точки перегиба х₁=-1/и х₂=1/, выпукл вверх на (выпукл вниз на (-;),();

290.2 точки перегиба х₁=--и х₂=, выпукл вверх на (выпукл вниз на (-),();

290.3 точки перегиба х₁=-1/и х₂=1/, выпукл вниз на (выпукл вверх на (-;),();

290.4 всюду выпукл вниз; 290.5 точки перегиба х₁=-1 и х₂=1, выпукл вверх на (-

(1;), выпукл вниз на(-1;1); 290.6 точка перегиба х=2, выпукл вверх на (-

выпукл вниз на(2;).

291. на интервале (,на (1; .

292.1 у=0 - горизонтальная асимптота.292.2 у=0 - горизонтальная асимптота;

292.3 вертикальные асимптоты, - горизонтальная асимптота;

292.4 -- горизонтальные асимптоты; 292.5 - горизонтальная асимптота

в левой полуплоскости;

292.6 - горизонтальная асимптота в правой полуплоскости;

293.1 293.2 293.3 в правой полуплоскости, в левой полуплоскости.