93.1 93.2
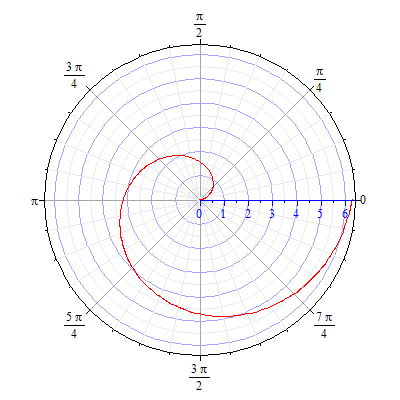
93.3 93.4
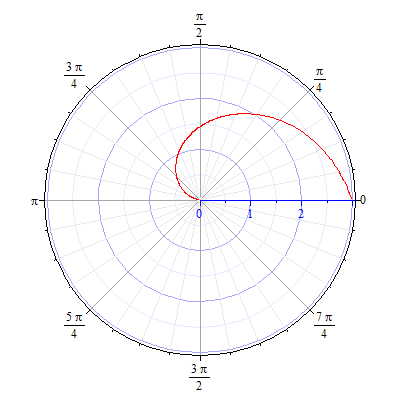
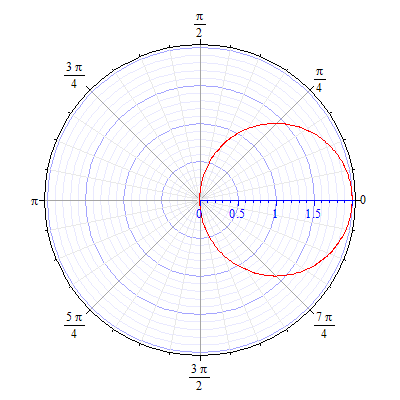
93.5 93.6
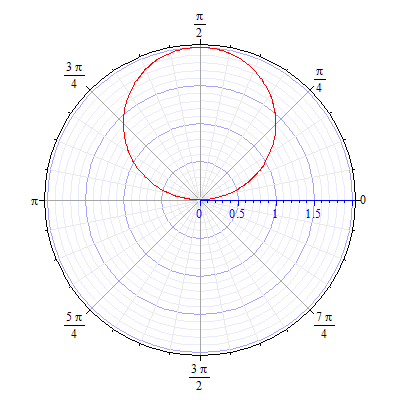
93.7 93.8
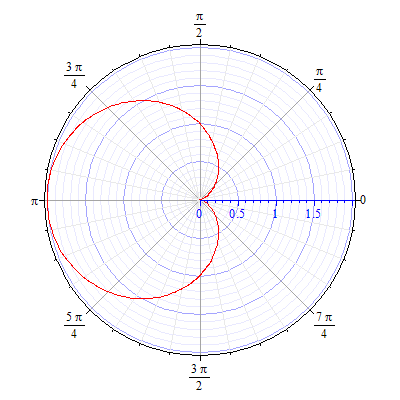
93.9
94.1
94.2
94.3
94.4
Элементы векторной алгебры.
95.1
95.2
95.3
96.1
96.2
96.3
98.1
98.2
98.3
99.№1, №5, №6. 100.1
100.2
101.
102.1
102.2
102.3
103.Да, так как
и 
104.1
104.2
105.1
105.2
105.3
105.44;105.5 3; 105.6 2;105.7
106.
107.
108
109.
110.
111.
112.
113.1
113.2
113.3
114.1
114.2
114.3
114.4
115.
116.1 
116.2-
116.3
116.4
Скалярное произведение векторов.
117.10;117.2 9;117.320.118.Вектор
перпендикулярен векторам
и
.119.
120.1
120.2
121.10;121.2
122.1
122.2
122.3
123.
124.15.125.1-4;125.20.
Векторное произведение.
126.1 -50; 126.2
126.3
127.1
127.2
127.3
127.4
127.5
128.
129.1
129.2
130.1
130.2
131.
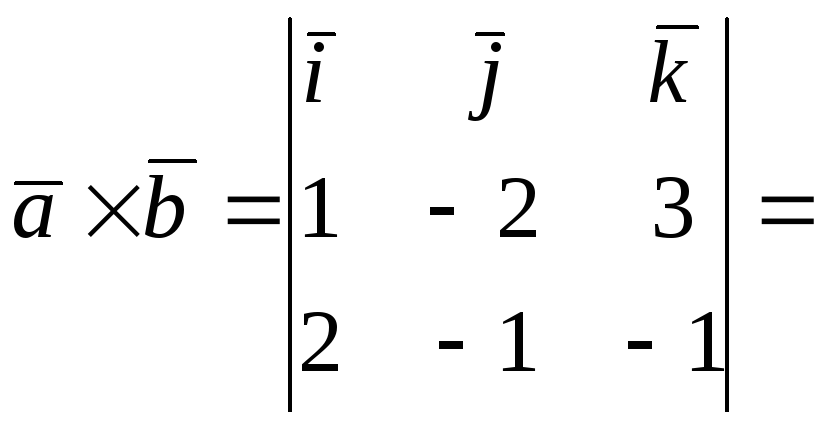
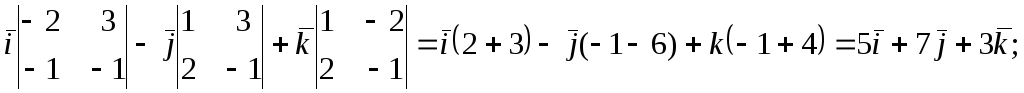
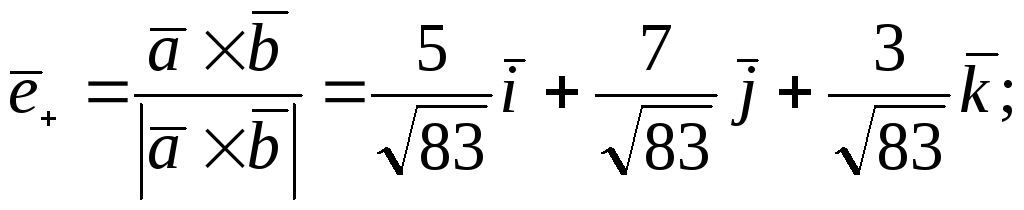
132.
См. 131. Все вектора -
где
произвольное
число.134.
135.
Смешанное произведение.
136.
.
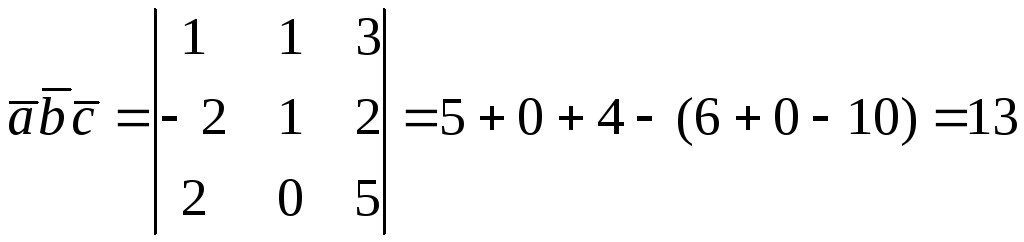137.1
137.2
138.Да, так как
139.Да.
Плоскости и прямые в пространстве.
140.1
140.2
140.3
140.4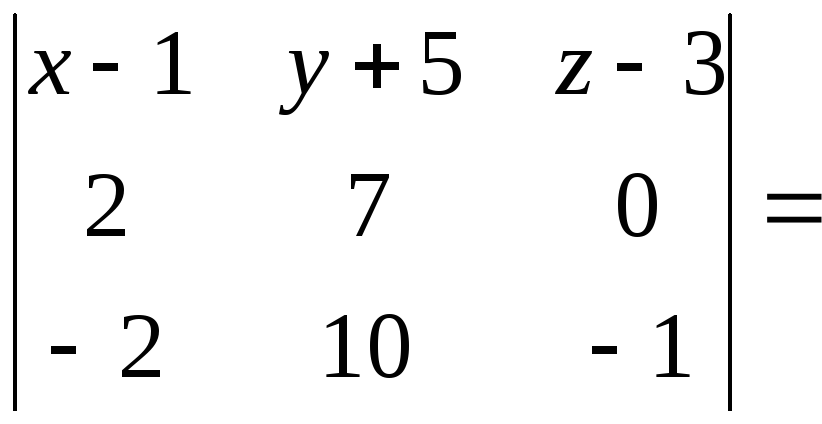
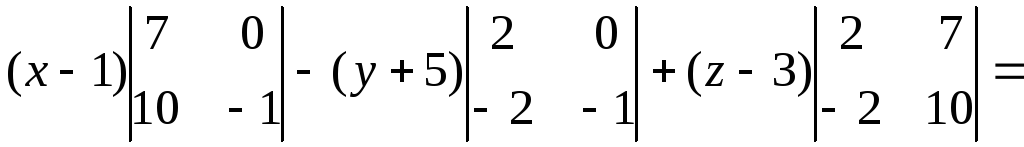
141.1
141.2
141.3
141.4
142.1Первая пара параллельны.
142.2 четвертая, пятая и шестая -
перпендикулярны.143.
144.1
144.2
145Нормальный вектор к заданной
плоскости
. Плоскость
имеет нормальный вектор
Плоскость
имеет нормальный вектор
Плоскость
имеет нормальный вектор
Следовательно
с плоскостью
и
осью
,
с плоскостью
и
с осью
,
с плоскостью
и
с осью
146.
147.1
или
147.2
или
147.3
или
147.4
или
147.5
или
147.6
или
148.1Для параллельности прямых необходимо
выполнение коллинеарности направляющих
векторов. 3 и 4 параллельны.148.2 Прямые
перпендикулярны, если скалярное
произведение направляющих векторов
равно нулю. 3 и 4 прямые перпендикулярны.
149.1 Направляющие вектора прямых:
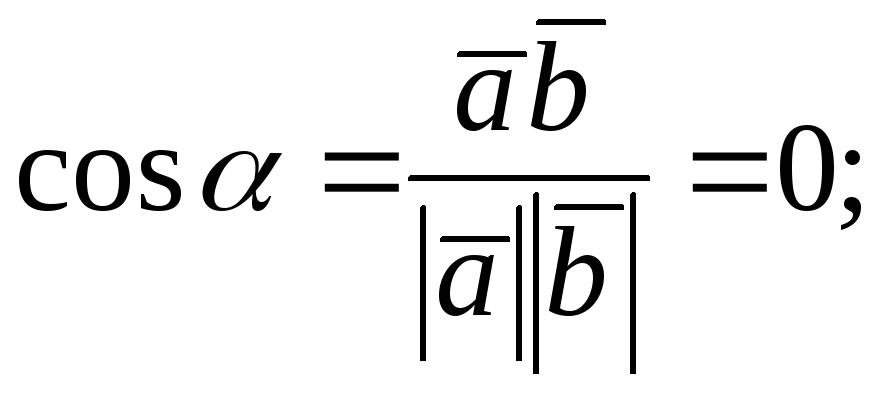
149.2 
149.3
150.1 
;150.3
. 151.Направляющий вектор прямой
.
С осью ОХ
с осью ОУ и
152.1 Пересекаются.Точка пересечения
152.2 Плоскость и прямая параллельны.152.3 Прямая лежит в плоскости.
152.4 Плоскость и прямая параллельны.152.5 Пересекаются.Точка пересечения
153. Проводим прямую через точку
перпендикулярно к заданной плоскости
(направляющий вектор прямой– вектор
нормали к плоскости), точка пересечения
с плоскостью и есть точка проекции
Р(1;0;2)
154. Вычисляем угол между направляющим
вектором прямой и нормалью к плоскости;
затем вычисляем синус требуемого угла.154.1
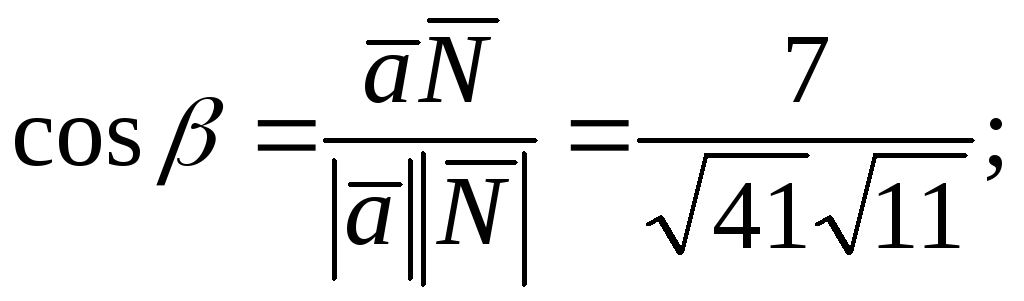
угол
между прямой и плоскостью.154.2
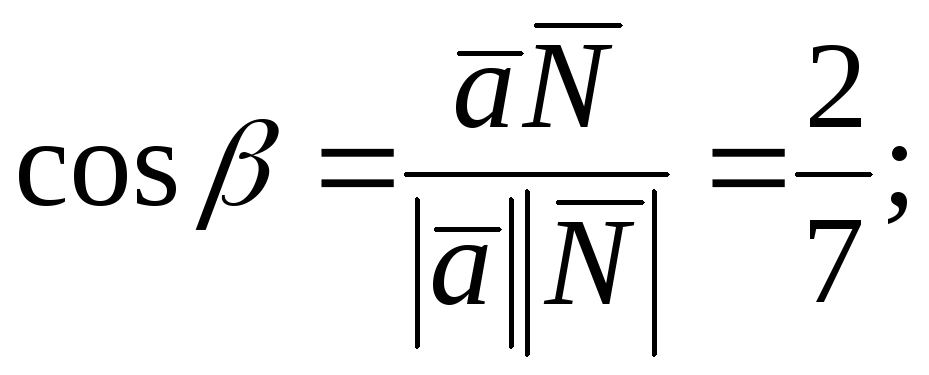
154.3
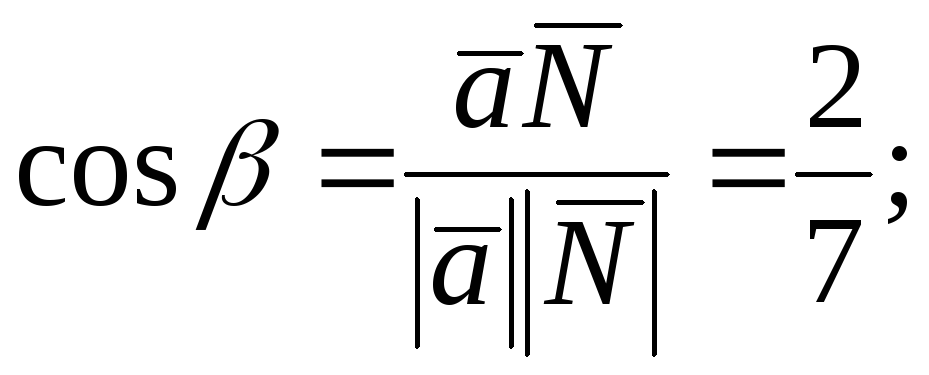
155.1С(-3;3;-3); 155.2 С(-15/2;3/4;-3/4).156. С
плоскостью х=0 :
С плоскостью у=0:
С плоскостьюz=0 :
Bведение в математический анализ.
157.
158.
159. 1)
;2)
;
160.1
160.2
160.3
160.4
161.1
161.2
161.3
161.4
162.1
162.2
162.3
(0;1).
163.1
163.2
163.3
163.4
163.5
163.6
164.1 утверждение верно; 164.2 неверно.
165.1.1
165.1.2
165.1.3
165.1.4
165.1.5
165.2.1
165.2.2
165.2.3
165.2.4
165.2.5
168. 1) функции различны т.к. у них разные области определения;
2) функции совпадают на указанной области определения;
3) функции различны т.к. у них разные области определения;
4) функции совпадают на указанной области определения.
169. 1) функции совпадают на указанной области определения;
2) функции различны;
3) функции совпадают на указанной области определения;
4) функции различны;
5) функции совпадают на указанной области определения;
6) функции различны;
7) функции совпадают на указанной области определения.
170. 1) четная; 2) четная; 3) четная; 4) нечетная.
171. 1) нечетная; 2) нечетная; 3) четная; 4) нечетная.
172. 1) четная; 2) общего вида; 3) общего вида; 4) общего вида; 5) общего вида;
6) четная; 7) нечетная; 8) общего вида; 9) четная; 10) общего вида; 11) четная;
12) четная; 13) четная; 14) четная; 15) нечетная; 16) четная; 17) нечетная;
18) четная; 19) четная; 20) четная.