
ЛАБ_ПРАК_MathCad
.pdfВ MathCad имеется функция root, которая позволяет находить корень из заданного интервала для любых уравнений. В частности для уравнений n-ой степени имеется два способа использования этой функции.
Примечание: В данной функции реализован метод Ньютона для нахождения корней уравнения, поэтому необходимо задавать начальное значение x, с которого и начинается поиск корня.
Первый способ. Задаем начальное значение x: x := −1.
Вызываем функцию:
X11 := root(y(x) ,x,−2 ,−1) ,
где y(x) – заданная левая часть уравнения y(x)=0; x – приближенное значение аргумента; (–2) – левый край интервала, которому принадлежит искомый корень; (–1) – правый край интервала.
Для просмотра полученного значения достаточно набрать X11=, получим:
 .
.
Оставшиеся два корня ищутся аналогично:
x := |
1 |
X12 |
:= |
root ( y(x) ,x , 1 |
, 2) |
x := |
3 |
X13 |
:= |
root ( y(x) ,x , 3 |
, 4) . |
В результате получим: |
|
|
|
||
|
|
X12 = 1.667 |
X13 = 4 . |
|
|
Второй способ. Задаем начальное значение x:=-1 и вызываем функцию:
41

X1 := root(y(x) ,x) .
Здесь интервалы не указываем, и функция ищет ближайший, к заданному значению, корень
X1 = −1.5 
 .
.
Для нахождения второго корня задаем значение x:=1 и исключаем из функции уже найденный корень:
X2 := root |
y(x) |
,x |
|
||||
|
|
|
|
||||
|
(x − X1) |
. |
|
||||
Получили значение: |
|
|
|
|
|
|
|
X2 = 1.667 |
|
. |
|
|
|
||
|
|
|
|
||||
|
|
|
|
||||
Третий корень ищем по аналогии: |
|
|
|
||||
x := 2 X3 := root |
|
y(x) |
|
,x |
X3 = 4 |
||
|
|
|
|
|
|||
(x − X1) (x − X2) |
. |
||||||
2.Выполним проверку полученного решения:
|
−3 |
= 0 |
|
y(4) = 0 |
|
|
|
y |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
− 15 |
|
y(1.667) = −0.015 y |
3 |
|
= −7.105 |
× 10 |
. |
||
Мы видим, что корень из интервала [1; 2] более точно найден функцией solve.
3. Трансцендентные уравнения можно решать графически, разбив уравнения на два более простых. Например, наше уравнение, заданное в виде
Y(x) := e2x + cos(3 x) ,
разобьем на два:
42
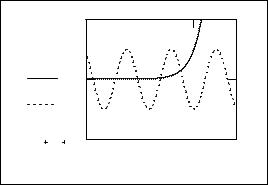
y1(x) := e2 x |
y2(x) := −cos(3 x) . |
Построим графики этих уравнений
2
2
y1( X)
0
y2( X)
− 1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
− 5 |
X |
2 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
По графику видно, что все корни уравнения лежат в интервале (-∞;0). Найдем несколько корней при помощи функции root (интервалы можно подобрать по графику):
x := 0 |
X1 := root(Y(x) ,x,−1 ,0) |
X1 = −0.621 |
||
x := −2 |
X2 := root(Y(x) ,x,−2 ,−1) |
X2 = −1.556 |
||
x := −3 |
X3 |
:= root(Y(x) ,x,−3 ,−2) |
X3 |
= −2.62 |
x := −4 |
X4 |
:= root(Y(x) ,x,−4 ,−3) |
X4 |
= −3.665 |
x := −10 |
X5 |
:= root(Y(x) ,x,−11,−10) |
X5 |
= −10.996 |
4.Выполним проверку полученного решения:
43
Y(X1) = 0 Y(X2) = 0 Y(X3) = 0
Y(X4) = −1.327× 10− 15 Y(X5) = 1.694× 10− 15 |
. |
|
Можно увидеть, что корни находятся с достаточно хорошей точностью, но с удалением от точки 0 точность начинает ухудшаться.
5. Зададим систему уравнений матрицей А и вектором правых частей f:
|
1 |
2 |
3 |
|
|
1 |
|
|
−1 |
1 |
5 |
|
|
−1 |
|
A := |
|
f := |
|
||||
|
1 |
−1 |
7 |
|
|
1 |
. |
Проведем исследование данной системы на разрешимость, для этого вычислим определитель матрицы А:
A = 36 
 .
.
Так как определитель матрицы не равен нулю, следовательно, наша система разрешима и имеет единственное решение.
Получим данное решение графически. Для этого построим каждую плоскость отдельно. В MathCad плоскости задаются так
z1(x,y) := (f0 − A0,0 x − A0,1 y)
z2(x,y) := (f1 − A1,0 x − A1,1 y)
z3(x,y) := (f2 − A2,0 x − A2,1 y)
.
44
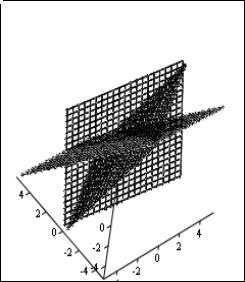
Графическое представление этих плоскостей имеет
вид
z1,z2,z3 |
. |
|
Видно, что в пересечении мы получим одну общую точку для всех плоскостей, которая и будет решением данной системы.
6. Решим систему уравнений матричным методом. Для этого найдем обратную матрицу:
B := A− 1 .
Теперь можно найти решение системы:
X := B f .
Вектор неизвестных имеет вид
45
1
X = 0 
0 .
7.Сделаем проверку:
|
1 |
|
|
1 |
|
|
−1 |
|
|
−1 |
|
A X = |
|
f = |
|
||
|
1 |
|
|
1 |
. |
ЛАБОРАТОРНАЯ РАБОТА № 4 «Метод наименьших квадратов. Регрессия»
Цель работы: Познакомить читателя с основами обработки экспериментальных данных с помощью фундаментальных численных методов и встроенных функций системы MathCad.
Рекомендуемая литература: [1-3, 7, 10].
46

Задание:
1.По заданной выборке построить аппроксимацию на основе заданного набора базисных функций с помощью метода наименьших квадратов.
2.На основе набора базисных функций, предложенного в пункте 1, построить регрессию для заданной выборки.
3.Провести сравнение результатов пункта 1 и пункта
2.
Варианты выборок находятся в таблице № 2 (см. лаб. работу №2), а вариант набора базисных функций представлены в таблице № 4.
Таблица № 4: Варианты набора базисных функций.
№ |
Набор базисных функций |
||
варианта |
|
|
|
1 |
|
2 |
|
1 |
cos(x); |
x3; |
1/x |
1 |
|
2 |
|
2 |
sin(x); |
ex; |
2x |
3 |
3x; |
1/x; |
cos(x) |
4 |
sin(x); |
ln(x); |
x2 |
5 |
x; |
cos(x); |
ex |
6 |
x3; |
sin(x); |
ln(x) |
7 |
cos(x); |
x2; |
2x |
8 |
sin(x); |
ln(x); |
3x |
9 |
cos(x); |
ex; |
1/x |
10 |
sin(x); |
1/x; |
2x |
11 |
cos(x); |
ln(x); |
1/x |
47
12 |
ex; |
ln(x); |
cos(x) |
13 |
sin(x); |
x3; |
ex |
14 |
cos(x); |
x2; |
ln(x) |
15 |
3x; |
x3; |
sin(x) |
16 |
3x; |
cos(x); |
x |
17 |
1/x; |
x2; |
cos(x) |
18 |
x; |
x3; |
sin(x) |
19 |
x2; |
e-x; |
cos(x) |
20 |
sin(x); |
ln(x); |
x |
21 |
1/x; |
x; |
cos(x) |
22 |
sin(x); |
x4; |
ex |
23 |
1/x; |
x4; |
cos(x) |
24 |
2x; |
sin(x); |
x4 |
25 |
ex; |
x4; |
cos(x) |
26 |
sin(x); |
ln(x); |
x4 |
27 |
cos(x); |
x4; |
ln(x) |
28 |
1/x; |
sin(x); |
x4 |
29 |
2x; |
cos(x); |
x4 |
30 |
1/x; |
sin(x); |
3x |
Пример выполнения задания:
Задание:
X Y
0 1
0.50.833
0.20.667
1.50.54
1 |
0.4 |
3 |
0.333 |
48
2.50.286
2 0.25
3.50.222
Базис произвольных функций: cos(x), x2, ex, ln(x+1),
sin(x).
1. Для удобства работы рекомендуем отсортировать выборки так, как это делалось в Лабораторной работе № 2. Получим:
|
0 |
|
|
1 |
|
|
0.2 |
|
|
0.667 |
|
|
0.5 |
|
|
0.833 |
|
|
|
|
|
||
|
1 |
|
|
0.4 |
|
x = 1.5 |
y = |
0.54 |
|
||
|
2 |
|
|
0.25 |
|
|
2.5 |
|
|
0.286 |
|
|
|
|
|
||
|
3 |
|
0.333 |
||
3.5 |
0.222 . |
||||
Зададим константы: N – номер последнего элемента выборки, n – число базисных функций минус единица и параметр i:
N := 8 n := 4 |
|
i := 0 ..N . |
|
Далее зададим набор функций: |
|
|
|
f0(x1) := cos (x1) f1(x1) := |
x12 |
f2(x1) := ex1 |
|
f3(x1) := ln(x1 + 1) |
f4(x1) := sin(x1) |
. |
|
|
|
|
|
Вычислим значения заданных функций в точках выборки x:
49
gi,0 := f0(xi) |
gi,1 := f1(xi) |
gi,2 := f2(xi) |
gi,3 := f3(xi) |
gi,4 := f4(xi) |
. |
Сформируем матрицу системы уравнений для нахождения коэффициентов пробной функции. Для этого зададим параметры:
i1 := 0 ..n |
j1 := 0 ..n. |
Формируем матрицу по формуле: |
|
N |
|
Mi1, j1 := ∑ (gk,i1 gk, j1) |
|
k =0 |
. |
Далее строим вектор правых частей для данной системы уравнений:
|
N |
|
fi1 := ∑ (yk2 gk2,i1) |
|
|
k2 |
=0 |
. |
|
|
|
Решаем нашу систему уравнений M*a=f (см. лаб. работа №3).
После чего получаем требуемую аппроксимацию: P(X) := a0 f0(X) + a1 f1(X) + a2 f2(X) + a3 f3(X) + a4 f4(X) .
График аппроксимации P(X) и экспериментальные точки представлены на рисунке
50
