Новосибирский государственный архитектурно-строительный университет (Сибстрин)

Кафедра прикладной

математики

Отчет по лабораторной работе №1

«Решение нелинейных алгебраических уравнений.

Методы решения систем линейный алгебраических уравнений.»

Выполнил: студ. гр.321

Гридин Александр

Проверил:

Федорченко И. А.

Новосибирск 2011.

1. Часть работы.

Постановка задачи. Задано нелинейное алгебраическое уравнение f(x)=0,5^х-1-(x-2)²+x=0. Решением уравнения является значение х^*, такое, что f(x^*)=0. Решить уравнение приближенным (итерационным) методом – значит построить последовательность {x_n} (n – номер итерации, т.е. приближения к решению), сходящуюся к точному решению уравнения: =x^*. Итерационный метод задается рекуррентной формулой, позволяющей определить последующее приближение по известным предыдущим. Итерационный процесс заканчивается, когда |x_n-x^*|<ε, где ε – точность метода, некоторое наперед заданное число. Перед тем, как начать решение уравнения итерационным методом, необходимо исследовать уравнение на наличие корней и для каждого из корней найти свой интервал изоляции [a,b], содержащего единственный корень уравнения. Условием того, что на отрезке [a,b] существует хотя бы один корень уравнения является f(a)f(b)<0.

Описание методов решения.

1. Метод деления отрезка пополам. Определяем середину отрезка [a,b]: c=(a+b)/2 и проверяем, какому из двух отрезков (a,c) или (c,b) принадлежит искомый корень, т.е. проверяем: f(a)f(c)<0 либо f(c)f(b)<0. Концы нового отрезка, которому принадлежит корень, обозначаем a, b и повторяем процедуру до тех пор, пока не будет достигнуто условие сходимости итерационного процесса: |b-a|<ε. Последующие границы интервала изоляции корня принимаем:

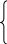c_i-1, если f(a_i-1)f(c_i-1)>0;

a_i =

a_i-1, в противном случае

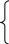
b_i-1, если f(a_i-1)f(c_i-1)>0;

b_i =

c_i-1, в противном случае i = 1,2,3…

c_i = (a_i+b_i)/2, i = 0,1,2…;

Вычисления оформляются в виде таблицы:

i	a	b	c	f(a)	f(c)	|b-a|
0
1
…

2. Метод простой итерации. Приведем исходное уравнение к виду, удобному для применения метода простой итерации: x = φ(x), где, например, φ(x) = x-τf(x). Параметр τ подберем таким образом, чтобы выполнялось достаточное условие сходимости метода: |φ'(x)|<1 для всех xє[a,b].Выберем начальное приближение х₀ = (a+b)/2. Следующие итерации находим по формуле: x_k+1 = φ(x_k)_. Часто τ берут в виде: τ=2/(M+m), где M = max(f '(x)), m = min(f '(x)). Условие окончания итерационного процесса |x_i-x_i-1|<ε.

i	x	|xi-xi-1|
0	x0	|x1-x0|
1	x1
…	…	…

3. Метод Ньютона. Выберем начальное приближение x₀є[a,b]:

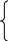a, если f(a)f ''(a)>0 ;

х₀ =

b, в противном случае.

Следующие итерации определяются о формуле x_k+1 = x_k-f(x_k)/f '(x_k). Условие окончания итерационного процесса |x_i-x_i-1|<ε. Вычисления оформляются в виде таблицы:

i	x	f(x)	f '(x)	|xi-xi-1|
0	x0	f(x0)	f '(x0)	|x1-xi-1|
1	x1	f(x1)	f '(x1)
…	…	…	…	…

Формулировка задания.

1. Исследовать функцию f(x)=0,5^х-1-(x-2)²+x=0 на наличие корней графически. Найти интервалы, на которых существует единственный корень уравнения.

2. Для каждого интервала изоляции [a,b] с заданной точностью ε=0.001 найти корни уравнения с использованием метода деления отрезка пополам, метода простой итерации, метода Ньютона.

Исследование функции f(x)=0,5^х-1-(x-2)²+x=0:

х	f(x)
-8	147
-7	39
-6	-7
-5	-23
-4	-25
-3	-21
-2	-15
-1	-9
0	-4
1	-0,5
2	1,25
3	1,125
4	-0,9375
5	-4,96875
6	-10,9844
7	-18,9922
8	-28,9961
9	-40,998
10	-54,999

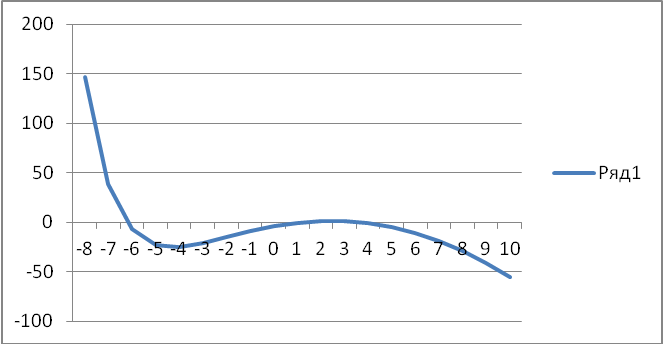
Интервал изоляции [-7;-6], [1;2], [3;4].

Решение уравнения.

1. Метод деления отрезка пополам.

Интервал изоляции [-7;-6].

i	a	b	c	F(a)	F(c)	|b-a|
0	-7	-6	-6,5	39	10,75967	1
1	-6,5	-6	-6,25	10,759668	0,796755	0,5
2	-6,25	-6	-6,125	0,7967554	-3,34813	0,25
3	-6,25	-6,125	-6,1875	0,7967554	-1,34018	0,125
4	-6,25	-6,1875	-6,21875	0,7967554	-0,28821	0,0625
5	-6,25	-6,21875	-6,23438	0,7967554	0,250101	0,03125
6	-6,23438	-6,21875	-6,22656	0,2501008	-0,02009	0,015625
7	-6,23438	-6,22656	-6,23047	0,2501008	0,114745	0,007813
8	-6,23047	-6,22656	-6,22852	0,1147445	0,047261	0,003906
9	-6,22852	-6,22656	-6,22754	0,0472615	0,013569	0,001953
10	-6,22754	-6,22656	-6,22705	0,0135686	-0,00327	0,000977

c=(-7-6)/2=-6,5

f(a)=0,5^-7-1-(-7-2)²-7=39

f(c)=0,5^-6,5-1-(-6,5-2)²-6,5=10,75967

f(a)* f(c)>0

Интервал изоляции [1;2].

i	a	b	c	F(a)	F(c)	|b-a|
0	1	2	1,5	-0,5	0,603553	1
1	1	1,5	1,25	-0,5	0,107948	0,5
2	1	1,25	1,125	-0,5	-0,18212	0,25
3	1,125	1,25	1,1875	-0,182123	-0,03359	0,125
4	1,1875	1,25	1,21875	-0,033593	0,038053	0,0625
5	1,1875	1,21875	1,203125	-0,033593	0,002449	0,03125
6	1,1875	1,203125	1,195313	-0,033593	-0,01552	0,015625
7	1,195313	1,203125	1,199219	-0,015518	-0,00652	0,007813
8	1,199219	1,203125	1,201172	-0,006521	-0,00203	0,003906
9	1,201172	1,203125	1,202148	-0,002033	0,000209	0,001953
10	1,201172	1,202148	1,20166	-0,002033	-0,00091	0,000977

c=(1+2)/2=1,5

f(a)=0,5¹-1-(2-2)²+1=-0,5

f(c)=0,5^1,5-1-(1,5-2)²+1,5=0,603553

f(a)* f(c)<0

Интервал изоляции [3;4].

i	a	b	c	F(a)	F(c)	|b-a|
0	3	4	3,5	1,125	0,338388	1
1	3,5	4	3,75	0,338388	-0,23817	0,5
2	3,5	3,75	3,625	0,338388	0,065427	0,25
3	3,625	3,75	3,6875	0,065427	-0,08254	0,125
4	3,625	3,6875	3,65625	0,065427	-0,0076	0,0625
5	3,625	3,65625	3,640625	0,065427	0,029154	0,03125
6	3,640625	3,65625	3,648438	0,029154	0,010838	0,015625
7	3,648438	3,65625	3,652344	0,010838	0,001635	0,007813
8	3,652344	3,65625	3,654297	0,001635	-0,00298	0,003906
9	3,652344	3,654297	3,65332	0,001635	-0,00067	0,001953
10	3,652344	3,65332	3,652832	0,001635	0,000482	0,000977

c=(3+4)/2=3,5

f(a)=0,5³-1-(3-2)²+3=1,125

f(c)=0,5^3,5-1-(3,5-2)²+3,5=0,338388

f(a)* f(c)>0

2. Метод Ньютона.

Условие начального приближения

f(x)*f''(x)>0

Интервал изоляции [-7;-6].

k	xi	Xi+1 –Xi	F(xi)	f'(xi)
0	-7	0,559358	39	-69,7228
1	-6,44064	0,193172	8,176259	-42,3264
2	-6,24747	0,020124	0,7077	-35,1676
3	-6,22735	0,000202	0,006952	-34,4783
4	-6,22715		6,91E-07	-34,4715

x	f	f''
-7	39	59,497986
-6	-7	28,748993

f(-7)=0,5^-7-1-(-7-2)²-7=39

f''(x)=0,5^x *ln0.5-5*x+5;

f''(x)=0.5^x*(ln0.5)²-5;

f'(-7)= 0,5^-7 *ln0.5-5*(-7)+5 =-69.7228

f(-7)* f''(-7)= 39*59.497986>0

x₁=x₀- f(x)/ f'(x)=-7+39/(-69.7228)=-6.44064

|X₁-X₀|=-0,55936>0,001

Интервал изоляции [1;2].

k	xi	Xi+1 –Xi	F(xi)	f'(xi)
0	1	0,188436	-0,5	2,653426
1	1,188436	0,01355	-0,03142	2,318991
2	1,201986	7,16E-05	-0,00016	2,294734
3	1,202057		-4,6E-09	2,294605

x	f	f''
1	-0,5	-1,759773
2	1,25	-1,879887

f(1)=-0.5

f''(x)=0,5^x *ln0.5-5*x+5;

f''(x)=0.5^x*(ln0.5)²-5;

f'(1) =-1.759773

f(1)* f''(1)= -0.5*(-1.759773)>0

x₁=x₀- f(x)/ f'(x)=1+0.5/2.653426=1.188436

|X₁-X₀|>0,001

Интервал изоляции [3;4].

k	xi	Xi+1 –Xi	F(xi)	f'(xi)
0	4	-0,30805	-0,9375	-3,04332
1	3,691948	-0,0383	-0,09336	-2,43753
2	3,653646	-0,00061	-0,00144	-2,36237
3	3,653036		-3,6E-07	-2,36117

x	f	f''
3	1,125	-1,939943
4	-0,9375	-1,969972

f(4)=-0.9375

f''(x)=0,5^x *ln0.5-5*x+5;

f''(x)=0.5^x*(ln0.5)²-5;

f'(4) =-3.04332

f(4)* f''(4)= -0.9375*(-1.939943)>0

x₁=x₀- f(x)/ f'(x)=4+0.9375/(-3.04332)=3.691948

|X₁-X₀|>0,001