3.Метод Чебышева.

x_k+1 =x_k – (f(x_k))/f'(x_k) - (f(x_k)* f''(x_k))/ 2(f'(x_k))³ ;

Интервал изоляции [-7;-6].

k	xk	Xk+1 –Xk	F(xk)	f'(xk)	f''(xk)
0	-7	0,562781	39	-69,7228	59,49799
1	-6,43722	0,192484	8,031607	-42,1906	39,63389
2	-6,24474	0,017682	0,61162	-35,0733	34,43372
3	-6,22705	-9,4E-05	-0,0032	-34,4683	33,98989
4	-6,22715		4,59E-05	-34,4715	33,99224

x₁ =-7 – (39)/(-69.7228) - 39* 59.49799/ 2(-69.7228)³=-6.43722

Интервал изоляции [1;2].

k	xk	Xk+1 –Xk	F(xk)	f'(xk)	f''(xk)
0	1	0,164886	-0,5	2,653426	-1,75977
1	1,164886	0,030778	-0,08653	2,361084	-1,78572
2	1,195665	0,005303	-0,01471	2,306053	-1,79024
3	1,200968	0,000904	-0,0025	2,296556	-1,79101
4	1,201872		-0,00043	2,294937	-1,79114

x₁ =1 – (-0.5)/( 2,653426) – (-0.5)* (-1,75977)/ 2(2,653426)³=1,164886

Интервал изоляции [3;4].

k	xk	Xk+1 –Xk	F(xk)	f'(xk)	f''(xk)
0	4	-0,27529	-0,9375	-3,04332	-1,96997
1	3,724709	-0,05873	-0,17427	-2,50185	-1,96366
2	3,665978	-0,01066	-0,03072	-2,38656	-1,96215
3	3,655322	-0,00188	-0,0054	-2,36566	-1,96187
4	3,653439		-0,00095	-2,36196	-1,96182

x₁ =4 – (-0,9375)/(-3,04332) -(-0,9375) * (-1.96997)/ 2(-3,04332)³=3,724709

Сравнение результатов, полученных по разным методам решения[3;4].

метод	значение	количество
решения	корня	итераций
деление отрезка пополам	3,652832	10
Метод Чебышева	3,653439	4
Ньютона	3,653036	3

Более выгоден метод Ньютона т.к. он потребовал меньшее количество итераций.

2.Часть работы.Слау.

П остановка задачи. Требуется найти решение системы m линейных уравнений, которая в общем виде записывается в виде

36х₁-5x₂-11х₃ -19х₄=-9

х₁+33х₂-11х₃-20х₄=-8

5х₁-х₂+26х₃-19х₄=-7

11х₁+4х₂-5х₃+21х₄=-6

В матричном виде эта система уравнений записывается так:

Ах=f, где

36 -5 -11 -19

А= 1 33 -11 -20 - матрица системы,

5 -1 26 -19

11 4 -5 21

-9 х1

b= -8 - вектор правых частей х= х2 - вектор неизвестных

-7 х3

-6 х4

Таким образом, задача состоит в том, чтобы при известных коэффициентах матрицы А и элементах вектора f найти такие значения (х₁,х₂… х_m)^T, что при подстановке их в систему уравнений они превращаются в тождества.

Необходимым и достаточным условием существования единственного решения СЛАУ является условие detА≠0. В случае равенства нулю определителя матрица называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.

Все методы решения линейных алгебраических задач можно разбить на два класса: прямые( методы Крамера, обратной матрицы и Гаусса) и итерационные( методы простой итерации, Якоби и Гаусса – Зейделя).

Метод обратной матрицы. Если detA≠0, то существует матрица А^-1, обратная к данной. Умножим исходную систему уравнений на обратную, получим: А^-1Ах=А^-1f.

Известно, что произведение обратной матрицы на исходную дает единичную матрицу Е, следовательно, получаем Ех=А^-1f, х=А^-1f

Решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Т.о., задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.

Метод простой итерации. Преобразуем исходную систему линейных уравнений Ах=f к эквивалентной системе вида:

х=хα+β, где

х – искомый вектор, а α и β – некоторые новые матрица и вектор соответственно. В качестве первого приближения можно взять х_i⁽⁰⁾=0. Следующие приближения находим по рекуррентным формулам

х^(к+1)=αх^(к)+β, к=0,1,2,…

Такой итерационный процесс будем называть методом простых итераций(МПИ). Достаточным условием сходимости МПИ к решению системы при любом начальном векторе х⁽⁰⁾ является требование ||α||<1, где ||α||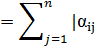 | - норма матрицы α.

Существует несколько способов построения порождающей матрицы α, для которой выполняется достаточное условие сходимости.

Метод Гаусса- Зейделя

В отличии от метода Якоби, в котором вычисление всех компонент вектора (k+1)-го приближения проводилось однообразно, в методе Гаусса- Зейделя для расчета i-й компоненты следующего приближения используется уже вычисленное на том, т.е. (k+1)-м шаге, новые значения первых i-1 компонент:

X₁^(k+1)=1/a₁₁(f₁-a₁₁^(k)-a₁₃x₃^(k)-…-a_1mx_m^(k))

X₂^(k+1)=1/a₂₂(f₂-a₂₁^(k+1)-a₂₃x₃^(k)-…-a_2mx_m^(k))

X_i^(k+1)=1/a_ij(f_i-a_i1^(k+1)-a_i2x₂^(k+1)-…-a_i,i-1x_i-1^(k+1)- a_i,i+1x_i+1^(k)-…-a_2mx_m^(k))

X_m^(k+1)=1/a_mm(f_m-a_m1^(k+1)-a_m2x₂^(k+1)-…-a_m,m-1x_m-1^(k+1))

Или, в компактном виде:

X_i^(k+1)=1/a_ij(f_i-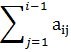 x_j^(k+1)- x_j^(k)), i=1,2…,m.

Достаточным условием сходимости этого метода, как и для метода Якоби, является условие диагонального преобладания:

/ a_ij/> 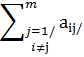, i=1,2…,m.

Формулировка задания.

Найти для своего варианта решение системы линейных уравнений Аx=b;

1. Методом обратной матрицы x= А^-1*b, используя функции Excel.

2. Методом простой итерации с точностью до 0,001

X_i^(k+1)=1/a_ij(b_i- x_j^(k)-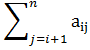 x_j^(k))

3. Методом Гаусса- Зейделя с точностью до 0,001

X_i^(k+1)=1/a_ij(b_i- x_j^(k)- x_j^(k))

Здесь k-номер итерации, n- количество уравнений, х_i⁽⁰⁾- начальное приближение. Оформить вычисления в виде таблиц.