
ЛАБ_ПРАК_MathCad
.pdfТаблица № 2: Варианты для лабораторной работы «Работа с файлами данных.
Сплайн-аппроксимация. Графика»
X |
|
Y |
X |
Y |
1 |
|
2 |
3 |
4 |
Вариант |
1 |
|
Вариант 2 |
|
5,036 |
|
0,3184 |
0,7551 |
1,64 |
1,241 |
|
0,3616 |
1,671 |
0,115 |
0,4048 |
|
0,419 |
1,204 |
3,511 |
0,7919 |
|
2,296 |
0,3196 |
2,797 |
0,1472 |
|
2,972 |
0,2828 |
1,345 |
1,32 |
|
0,76 |
1,911 |
2,131 |
0,258 |
|
0,3144 |
2,705 |
0,6963 |
0,899 |
|
0,3819 |
0,891 |
2,98 |
1,806 |
|
0,9785 |
1,47 |
1,075 |
1,446 |
|
2,966 |
2,31 |
0,6558 |
Вариант |
3 |
|
Вариант 4 |
|
0,008726 |
|
1,757 |
0,08349 |
0,5325 |
1,607 |
|
1,158 |
0,2392 |
0,8898 |
3,563 |
|
1,533 |
0,704 |
0,689 |
0,477 |
|
0,717 |
0,07632 |
0,1324 |
0,3834 |
|
0,813 |
0,7146 |
0,244 |
1,355 |
|
0,4959 |
0,7849 |
0,525 |
0,6015 |
|
0,9044 |
0,2219 |
1,263 |
2,162 |
|
0,1695 |
0,2279 |
0,1329 |
0,1844 |
|
0,4679 |
1,214 |
1,187 |
0,4939 |
|
2,899 |
0,2907 |
0,1417 |
Вариант |
5 |
|
Вариант 6 |
|
0,09998 |
|
0,1452 |
0,6176 |
0,8304 |
0,03405 |
|
1,171 |
0,6983 |
0,95 |
0,4661 |
|
3,586 |
0,3955 |
4,549 |
0,5829 |
|
0,9291 |
0,03916 |
0,1433 |
21
1 |
|
2 |
3 |
4 |
0,1119 |
|
3,437 |
0,7076 |
0,3536 |
0,1879 |
|
0,1517 |
1,273 |
0,5018 |
0,002423 |
|
0,9023 |
0,4185 |
0,5747 |
0,3713 |
|
0,4867 |
0,352 |
0,9625 |
0,9992 |
|
0,1317 |
2,267 |
0,06405 |
0,1315 |
|
0,5139 |
1,016 |
0,03619 |
Вариант |
7 |
|
Вариант 8 |
|
0,7388 |
|
0,2294 |
0,0443 |
0,6852 |
0,2943 |
|
0,5212 |
0,4131 |
1,311 |
3,572 |
|
0,5578 |
1,031 |
0,4316 |
0,9722 |
|
0,3924 |
0,7921 |
1,32 |
0,401 |
|
4,536 |
0,173 |
0,7685 |
0,1338 |
|
1,063 |
2,005 |
1,035 |
0,5464 |
|
0,2574 |
0,3974 |
0,7337 |
0,2235 |
|
0,138 |
1,224 |
0,8975 |
0,5896 |
|
0,3175 |
0,3318 |
3,553 |
0,2228 |
|
0,111 |
0,3803 |
0,5108 |
Вариант |
9 |
|
Вариант 10 |
|
0,3869 |
|
0,6181 |
2,457 |
0,04163 |
0,2324 |
|
0,2458 |
1,257 |
0,2356 |
0,4212 |
|
1,606 |
1,415 |
0,1984 |
1,425 |
|
0,2241 |
0,09192 |
1,976 |
0,6457 |
|
0,1623 |
1,232 |
3,868 |
0,4979 |
|
0,4594 |
0,3304 |
0,287 |
0,2157 |
|
0,4781 |
0,07192 |
0,102 |
1,342 |
|
1,37 |
0,0619 |
0,2614 |
0,5357 |
|
0,2357 |
1,428 |
0,4559 |
0,2696 |
|
0,3336 |
0,425 |
0,3782 |
Вариант |
11 |
|
Вариант 12 |
|
1,445 |
|
2,482 |
1,076 |
1,113 |
1,476 |
|
0,1547 |
0,07766 |
1,586 |
0,277 |
|
1,167 |
0,07734 |
2,058 |
22
1 |
|
2 |
3 |
4 |
0,6433 |
|
0,7411 |
1,906 |
0,111 |
0,02564 |
|
1,634 |
1,33 |
1,489 |
1,416 |
|
0,004966 |
0,1916 |
0,5738 |
0,1483 |
|
0,43 |
1,176 |
0,8502 |
1,248 |
|
1,73 |
4,212 |
0,1446 |
0,1524 |
|
1,278 |
1,639 |
1,306 |
1,405 |
|
0,1739 |
0,8814 |
0,3793 |
Вариант |
13 |
|
Вариант 14 |
|
0,2355 |
|
0,9809 |
0,2398 |
1,529 |
0,9622 |
|
1,444 |
2,62 |
0,2572 |
0,2887 |
|
1,448 |
0,3316 |
0,58 |
0,246 |
|
0,02911 |
1,857 |
0,1585 |
1,582 |
|
3,738 |
0,04041 |
0,6119 |
0,1365 |
|
1,866 |
0,9748 |
0,1386 |
0,498 |
|
4,635 |
0,01389 |
1,465 |
0,6439 |
|
0,4358 |
0,9287 |
0,9814 |
0,03925 |
|
0,8716 |
0,7557 |
3,319 |
0,452 |
|
2,376 |
1,148 |
0,9123 |
Вариант |
15 |
|
Вариант 16 |
|
0,5673 |
|
0,3541 |
0,3837 |
0,3035 |
0,1254 |
|
0,415 |
0,4156 |
2,061 |
0,5927 |
|
0,6183 |
1,135 |
0,9707 |
0,01298 |
|
2,889 |
4,117 |
0,08746 |
0,2282 |
|
1,333 |
1,886 |
3,401 |
1,23 |
|
0,1455 |
0,1182 |
0,7929 |
0,1321 |
|
2,412 |
0,1581 |
1,461 |
0,5219 |
|
0,3399 |
0,2785 |
1,835 |
2,713 |
|
0,1444 |
0,4791 |
0,6828 |
0,421 |
|
1,215 |
1,47 |
0,2789 |
Вариант |
17 |
|
Вариант 18 |
|
0,4775 |
|
0,4342 |
0,04178 |
0,1104 |
0,1289 |
|
0,1861 |
0,4733 |
0,5984 |
23
1 |
|
2 |
3 |
4 |
0,3165 |
|
0,1357 |
0,2763 |
0,6424 |
0,1297 |
|
0,09062 |
1,019 |
0,0006657 |
1,667 |
|
0,8123 |
0,4856 |
0,1408 |
0,8743 |
|
1,028 |
0,6943 |
1,9 |
0,9448 |
|
0,8407 |
0,4041 |
1,245 |
1,483 |
|
6,97 |
0,2867 |
0,02633 |
0,1365 |
|
0,2542 |
0,6276 |
0,3299 |
0,3854 |
|
2,385 |
3,725 |
0,434 |
Вариант |
19 |
|
Вариант 20 |
|
1,038 |
|
0,3761 |
0,4618 |
0,2039 |
4,851 |
|
1,851 |
2,206 |
0,2035 |
0,1626 |
|
2,996 |
0,487 |
0,1066 |
1,176 |
|
3,945 |
1,78 |
1,298 |
0,447 |
|
0,4301 |
0,0867 |
1,457 |
1,641 |
|
0,08886 |
1,45 |
0,1324 |
0,215 |
|
0,8315 |
0,05348 |
0,167 |
0,4604 |
|
1,402 |
2,307 |
3,164 |
0,6255 |
|
0,4203 |
0,8225 |
1,677 |
0,2734 |
|
3,74 |
0,6944 |
0,7921 |
Вариант |
21 |
|
Вариант 22 |
|
0,6255 |
|
1,957 |
0,42 |
1,847 |
0,414 |
|
0,591 |
0,4541 |
0,3955 |
0,3504 |
|
0,7613 |
0,881 |
1,051 |
0,5171 |
|
1,189 |
0,1609 |
0,2232 |
0,2739 |
|
1,061 |
0,9497 |
0,01827 |
1,254 |
|
0,4925 |
0,08356 |
1,207 |
1,301 |
|
0,01553 |
0,2235 |
0,1329 |
0,5905 |
|
1,872 |
0,7689 |
2,27 |
1,757 |
|
0,3367 |
1,114 |
1,925 |
1,782 |
|
0,2517 |
1,111 |
1,163 |
Вариант |
23 |
|
Вариант 24 |
|
0,05358 |
|
0,4713 |
1,343 |
0,5867 |
24
1 |
|
2 |
3 |
4 |
0,08409 |
|
0,37 |
0,8123 |
0,6432 |
1,118 |
|
0,5614 |
0,7556 |
0,3472 |
0,6718 |
|
0,595 |
0,1662 |
0,3092 |
0,3511 |
|
1,386 |
0,4843 |
0,08879 |
0,6002 |
|
0,7008 |
0,1702 |
0,2247 |
0,3884 |
|
0,3967 |
1,459 |
0,9196 |
0,1185 |
|
0,4678 |
0,6872 |
2,915 |
0,3551 |
|
0,2224 |
1,503 |
6,967 |
0,43 |
|
0,01105 |
2,05 |
0,2767 |
Вариант |
25 |
|
Вариант 26 |
|
1,277 |
|
0,4582 |
1,531 |
0,8438 |
0,4443 |
|
0,5201 |
0,03737 |
0,7658 |
1,068 |
|
0,6752 |
2,704 |
0,2856 |
0,3797 |
|
0,791 |
2,177 |
0,575 |
0,4053 |
|
0,06085 |
1,531 |
0,08036 |
0,5317 |
|
1,365 |
0,1101 |
0,1528 |
0,2266 |
|
0,3108 |
0,2463 |
0,7043 |
0,3604 |
|
0,4651 |
3,187 |
0,2885 |
0,1642 |
|
0,4397 |
0,2608 |
1,35 |
0,4164 |
|
0,5804 |
1,152 |
0,2309 |
Вариант |
27 |
|
Вариант 28 |
|
0,06992 |
|
0,7985 |
0,2822 |
0,002487 |
0,24 |
|
0,003961 |
0,3778 |
1,572 |
0,3049 |
|
0,5042 |
3,874 |
0,9365 |
0,8721 |
|
1,738 |
1,734 |
0,5376 |
0,8945 |
|
1,09 |
0,111 |
0,04029 |
1,676 |
|
0,421 |
0,2199 |
0,9533 |
0,1216 |
|
0,8412 |
0,7303 |
2,092 |
1,408 |
|
0,3839 |
0,4475 |
3,042 |
1,913 |
|
0,691 |
0,0342 |
0,2703 |
0,3358 |
|
0,2175 |
1,309 |
6,265 |
|
|
|
|
|
25
|
|
1 |
|
|
2 |
|
3 |
4 |
|
|
Вариант |
29 |
|
|
Вариант 30 |
|
|
|
|
0,4581 |
|
5,343 |
0,3736 |
0,1385 |
||
|
|
0,675 |
|
0,9686 |
1,983 |
3,208 |
||
|
|
0,5772 |
|
0,1876 |
0,3208 |
0,06537 |
||
|
|
1,419 |
|
0,1141 |
1,703 |
1,784 |
||
|
|
0,2294 |
|
0,4255 |
1,119 |
2,124 |
||
|
|
0,1437 |
|
0,3062 |
0,06298 |
2,112 |
||
|
|
0,1022 |
|
0,04343 |
0,3105 |
0,539 |
||
|
|
0,9088 |
|
1,002 |
0,5347 |
0,3094 |
||
|
|
1,557 |
|
0,09918 |
0,5281 |
0,3968 |
||
|
|
0,1828 |
|
0,78 |
0,5095 |
0,21 |
||
Пример выполнения задания: |
|
|||||||
Задание: |
|
|
|
|
||||
|
|
X |
|
Y |
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
0.5 |
|
|
0.833 |
|
|
|
|
|
0.2 |
|
|
0.667 |
|
|
|
|
|
1.5 |
|
|
0.54 |
|
|
|
|
|
1 |
|
|
0.4 |
|
|
|
|
|
3 |
|
|
0.333 |
|
|
|
|
|
2.5 |
|
|
0.286 |
|
|
|
|
|
2 |
|
|
0.25 |
|
|
|
|
|
3.5 |
|
|
0.222 |
|
|
|
|
Примечание: Будем работать на диске С: в папке
Student.
1. С помощью встроенного редактора (Блокнот, WordPad, Word и т.п.) создаем два файла x.txt и y.txt, в которые записываем наши значения. В зависимости от того,
26
как были записаны значения (в строку или в столбик) так они
ибудут прочитаны.
2.Чтение данных из файлов осуществляется следующим образом:
x:=READPRN(”C:\Student\x.txt”) y:=READPRN(”C:\Student\y.txt”).
3.Сформируем матрицу. Для этого задаем параметр i
i:=0.. 8
и записываем следующие формулы
Mi ,0 := xi |
Mi ,1 := yi . |
4. Для сортировки матрицы по столбцу, воспользуемся встроенной функцией
M1 := csort(M,0) ,
где в csort(M,0) первый параметр – сортируемая матрица, а второй – столбец по которому идет сортировка.
5.Запись полученной матрицы в файл производится с помощью команды
WRITEPRN(”C:\Student\m.txt”):=M1 .
6.Для построения линейного сплайна расформируем отсортированную матрицу M1 на два вектора vx и vy. Для этого выполним следующие операции
|
i:=0.. 8 |
vxi := M1i ,0 |
vyi := M1i ,1 . |
Далее получим коэффициенты для линейного сплайна Sl с помощью встроенной функции пользователя lspline:
Sl := lspline(vx,vy) .
27
Сформируем значения сплайна fl в точке x с помощью встроенной функции пользователя interp
fl( X) := interp(Sl,vx,vy , X) ,
где Sl – полученные ранее коэффициенты сплайна; vx, vy – исходные вектора; X – переменная сплайна.
Для построения графиков в пакете MathCad существуют встроенные функции пользователя для вызова графиков различного типа (декартова система координат двух- и трехмерная, полярная система и т.д.). Соответствующие встроенные функции находятся на панели инструментов: //Вид//Панели инструментов// График.
Для наших целей выбираем двухмерную декартову систему координат
.
Заполняем нижнее поле ввода: X,vx; верхнее поле: fl(X),vy и получаем
28
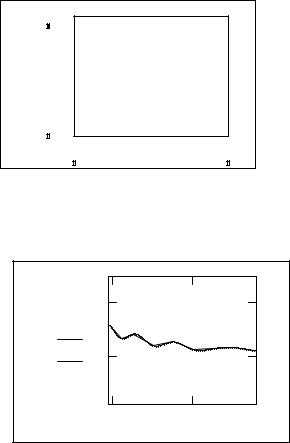
fl(X)
vy
|
|
|
X , vx |
|
. |
Теперь следует определить пределы изменения по оси
X и Y. По оси X: min(vx)-0.1 и max(vx)+0.1; по оси Y: min(vy)-2
и max(vy)+2. Получаем
max( vy)+2
2
fl(z)
vy
0
min( vy)−2
0 |
2 |
|
min( vx)−0.1 |
z, vx max( vx)+0.1 |
. |
|
|
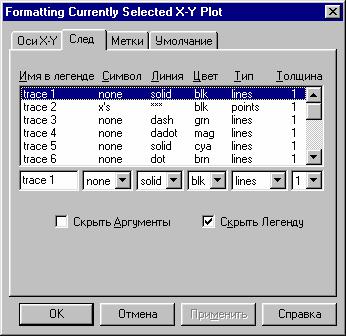
Как видно, графики практически совпали. Значения vy заданы в виде 10 точек, поэтому хотелось бы изобразить их отдельными точками. Для этого установим курсор мыши на выделенном графике и вызовем контекстное меню (щелчек правой кнопки мыши). В контекстном меню выберем «Формат…». Получим диалоговое окно «Формат», в котором открываем вторую закладку «След» (рис.2). В первом столбце указанной таблицы номер изображаемой линии. Во втором – символ, которым эта линия изображается (нет
29
символа, крестики и т.п.). В третьем – вид линии (сплошная, пунктирная и т.п.). В четвертом – цвет линии. В пятом – тип линии (линией, точками и т.д.). В последнем столбце указывается толщина линии в пунктах.
 .
.
рис. 2.
У нас график vy задан вторым, поэтому установим настройки для второй линии как указано на рис.2 и получим
30
