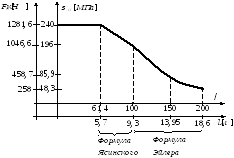4. 6.1. Задача 6.1.

Дано: Сжатая стойка, материал Ст 3.,

R = 200 МПа.

Требуется:

1. С помощью таблицы коэффициентов продольного изгиба подобрать поперечное сечение стойки заданной формы.

2. Подобранное сечение проверить на прочность при наличии ослабления A_nt = 0,85 · A_br.

3. Определить критическую силу и коэффициент запаса устойчивости.

4. Для подобранного сечения построить график зависимости критической силы и критического напряжения от длины и гибкости стержня, изменяя гибкость от 0 до 200.

Решение

Расчёт центрально сжатого стержня на устойчивость производят методом последовательных приближений.

1. Зададим коэффициент продольного изгиба в первом приближении φ = 0,6. Запишем условие устойчивости и выразим из него площадь поперечного сечения стойки.

.

По сортаменту выбираем швеллер с ближайшим значением площади, а именно 2[№27: А = 35,2 см², I_y = 262 см⁴,

i_z = i_x= 10,9 см, b = 95 мм, z₀ = 2,47 см.

В данном случае потеря устойчивости будет происходить в плоскости YOX, т.к. очевидно, что I_y < I _z => i_y < i_z.

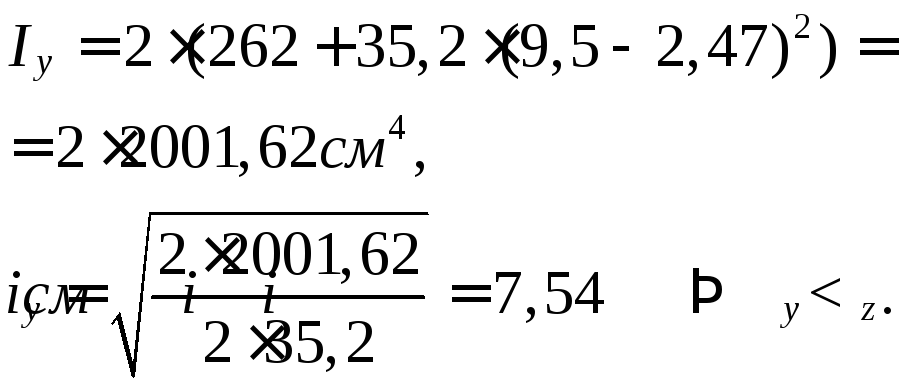
С помощью СНиП определяется значение коэффициента продольного изгиба φ.

λ = 50 φ = 0,869,

λ = 60 φ = 0,827.

Для λ=55,7 определим φ с помощью интерполяции:

Выполним проверку устойчивости

.

Выполним еще одну итерацию. Во втором приближении коэффициент продольного изгиба находится как среднеарифметическое значение между заданным в начале предыдущей итерации (φ = 0,6) и вычисленным для швеллера №27 (φ = 0,846). . Последующие вычисления аналогичны вычислениям, изложенным выше.

.

По сортаменту выбираем швеллер с ближайшим значением площади, а именно 2[№22: А = 26,7 см², I_y = 151 см⁴,

i_z = i_x = 8,89 см, b = 82 мм, z₀ = 2,21 см.

Определим значение момента инерции относительно оси y

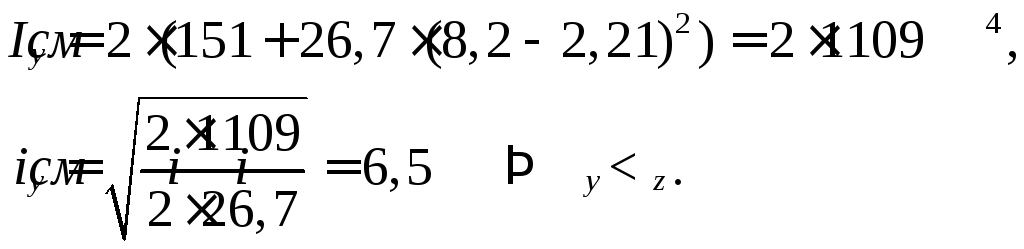
С помощью СНиП определяется значение коэффициента продольного изгиба φ.

λ = 60 φ = 0,827,

λ = 70 φ = 0,782.

Для λ = 64,6 определим φ с помощью интерполяции: .

Выполним проверку устойчивости

.

Проверим 2[№20: А = 23,4 см², I_y = 113 см⁴, i_z = i_x = 8,07см,

b = 76 мм, z₀ = 2,07 см.

Определим значение момента инерции относительно оси y

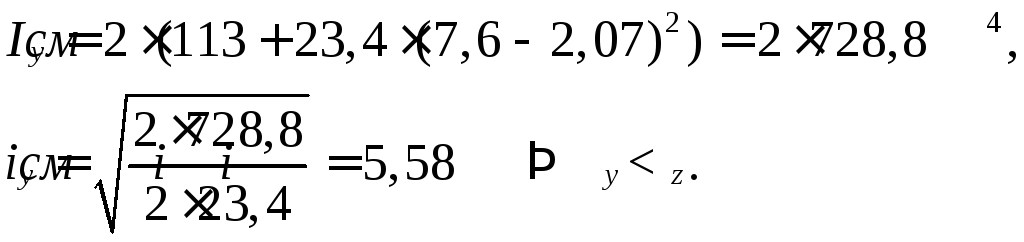
С помощью СНиП определяется значение коэффициента продольного изгиба φ.

λ = 70 φ = 0,782,

λ = 80 φ = 0,734.

Для λ = 75,3 определим φ с помощью интерполяции: .

Выполним проверку устойчивости

.

Окончательно принимаем 2[№22. Расчет на устойчивость закончен.

2. Выполним проверку прочности подобранного сечения при наличии ослабления A_nt = 0,85 · A_br.

.

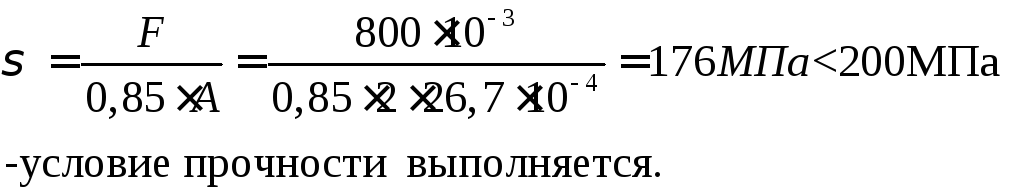
Сечение, подобранное из условия устойчивости, удовлетворяет условию прочности, корректировку сечения проводить не требуется.

3. Определение критической силу и коэффициента запаса устойчивости.

Предельная гибкость для Ст 3.

Сравним гибкость, найденную в п.1. расчета на устойчивость с предельной гибкостью: λ = 64,6 < 100. В случае, когда гибкость стержня меньше предельной гибкости определение критической силы производят с помощью эмпирической зависимости Ясинского.

Определим коэффициент запаса устойчивости.

4. Для подобранного сечения построим график зависимости критической силы и критического напряжения от длины и гибкости стержня, изменяя гибкость от 0 до 200.

Поперечное сечение состоит из двух прокатных профилей 2[№22: площадь одного профиля А = 26,7см², минимальный момент инерции всего сечения, состоящего из двух профилей I_min = 2218см⁴ и минимальный радиус инерции i_min = 6,5см.

Задавая гибкость стержня 62,4 (λ_min для СТ 3.), 100, 150, 200 будем получать соответствующую этим гибкостям длину стержня.

В интервале 61,4 ≤ λ ≤ 100 определение критических значений следует производить с помощью формулы Ясинского.

В интервале 100 ≤ λ ≤ 200 определение критических значений следует производить с помощью формулы Эйлера.

Для удобства сведём результаты расчёта в таблицу.

λ	l [м]	σcr [МПа]	Fcr [кН]
61,4	5,7	240	1281,6
64,6	6	235,04	1255,2
100	9,3	196	1046,6
150	13,95	85,9	458,7
200	18,6	48,3	258