Калинин / Приборостроителям / Математика 1 (16)

ВАРИАНТ ЧЕТВЕРТЫЙ

(для студентов, номера личных дел которых оканчиваются цифрой 4).

Контрольная работа № 1

1. По формулам Крамера решить систему линейных уравнений:

2. Найти предел:

3. Найти производную функции:

4.Найти катет прямоугольного треугольника наибольшей площади, если сумма этого катета и гипотенузы данного треуголь­ника равна 6 см.

5.Составить уравнение касательной к кривой , проходящей через точку с координатами (—3; 0). Сделать чертеж.

6.Исследовать функцию и схематично построить ее график.

Контрольная работа № 2

1.Найти неопределенный интеграл:

Вычислить определенные интегралы:

2.

3.

4. Решить дифференциальное уравнение:

5. Вычислить площадь фигуры, ограниченной линиями:

6. Экспериментальные данные о значениях переменных х и у приведены в таблице:

xi 1	3	5	6	8	11	13
yi	1,3	1,0	0,8	0,5	0,4	0,2

В результате их выравнивания получена функция .Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью у = ах + b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

7. Используя разложение подынтегральной функции в ряд Маклорена, вычислить с точностью до 0,001 значение определен­ного интеграла:

.

Контрольная работа №1.

2) - для раскрытия неопределенности используем правило Лопиталя-Бернулли и продифференцируем по отдельности числитель и знаменатель.

.

.

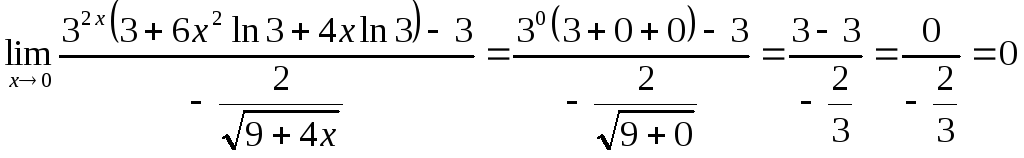3.

Производная суммы есть сумма производных слагаемых:

.

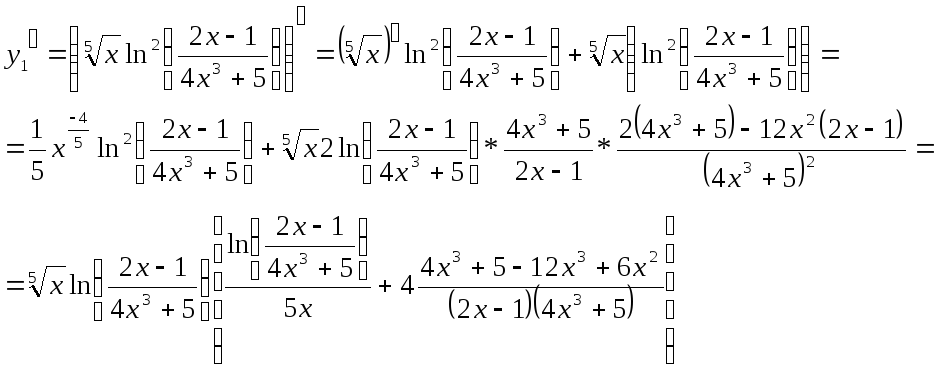
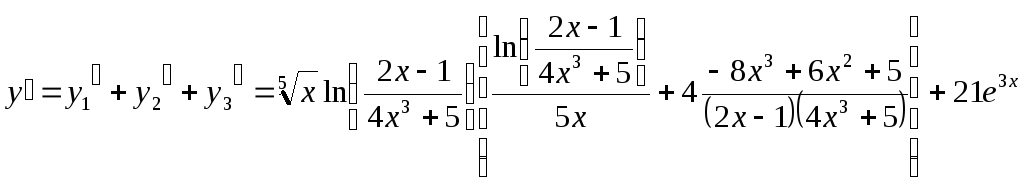4. Площадь прямоугольного треугольника ; при a=0, S=0; a=6см, S=0.

- по теореме Пифагора.

- условие задачи, тогда см.

Следовательно .

.

Считая а переменным , найдем экстремум функции:

;

.

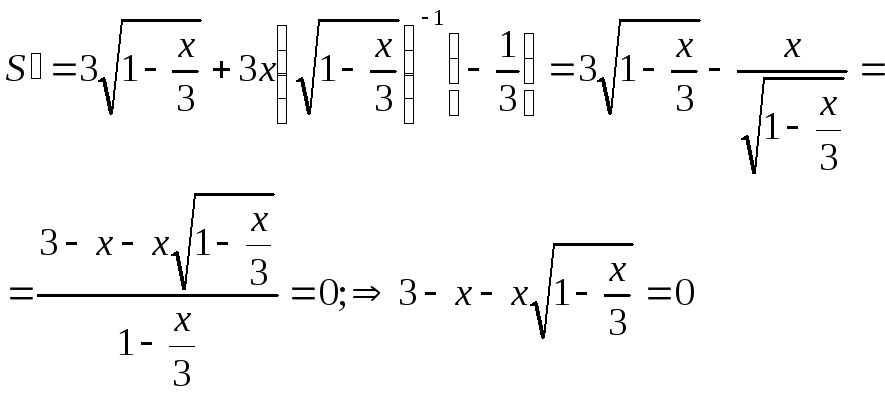
- методом итерационного подбора ,

x₃ – не удовлетворяет условию (длина катета величина строго положительная).

см. – мах;

.

см² (максимальна) при длине катета см, гипотенузы см.

катет см.

1. Главный определитель системы:

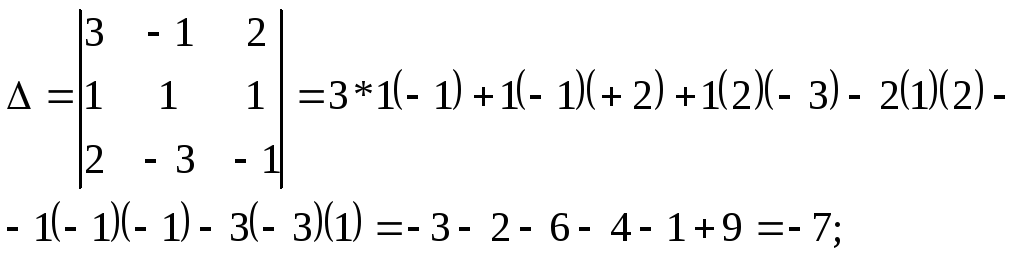
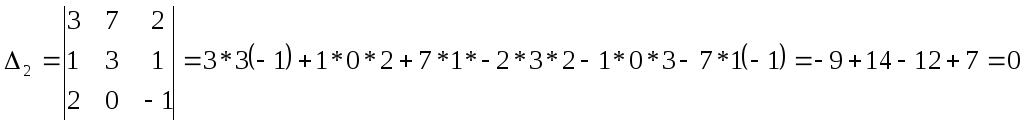
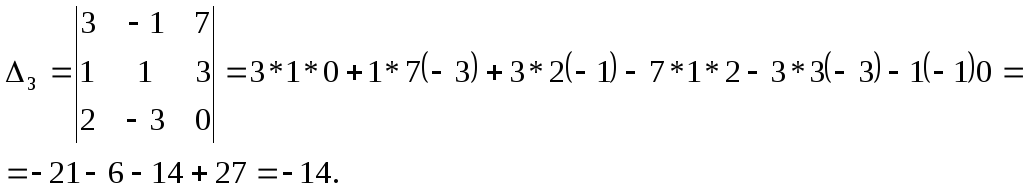
Формулы Крамера:

;

;

.

Проверка подстановкой:

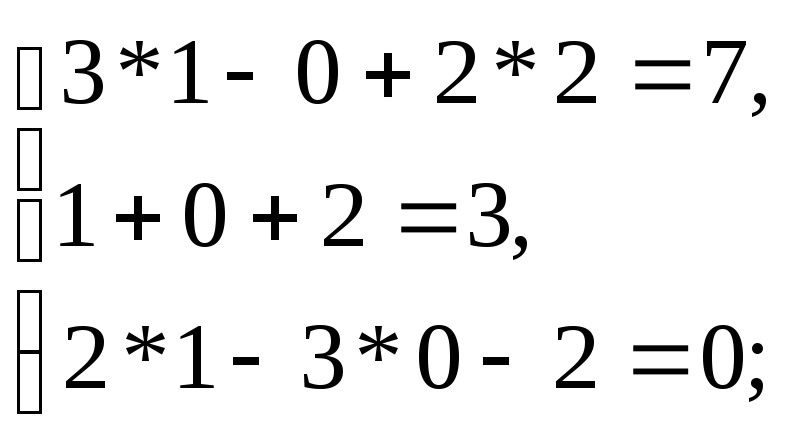
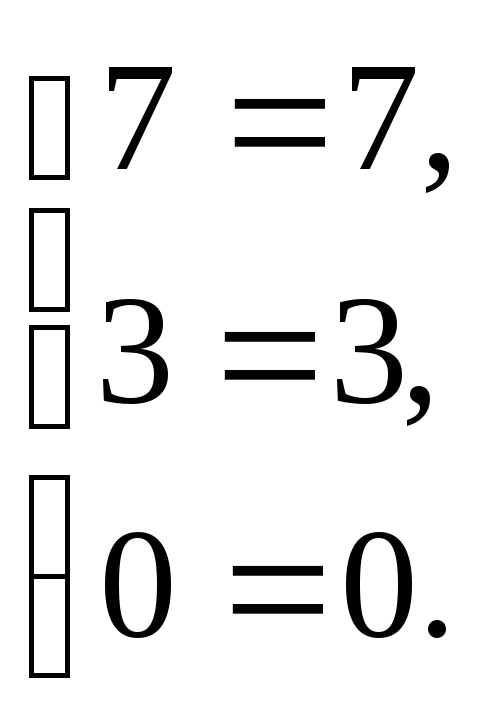
Контрольная работа №2. (Табличные интегралы по М.Л. Смолянский «Таблица неопределенных интегралов», М. «Наука» 1967.)

1.

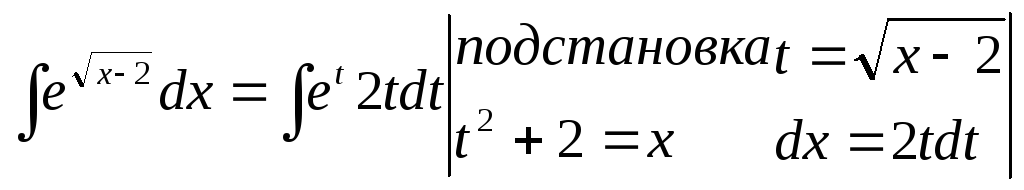
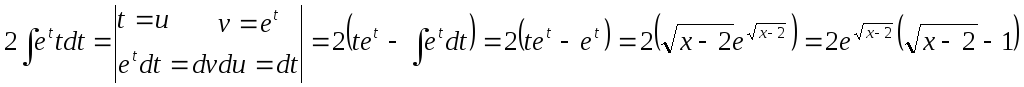(интегрировали по частям)

2.

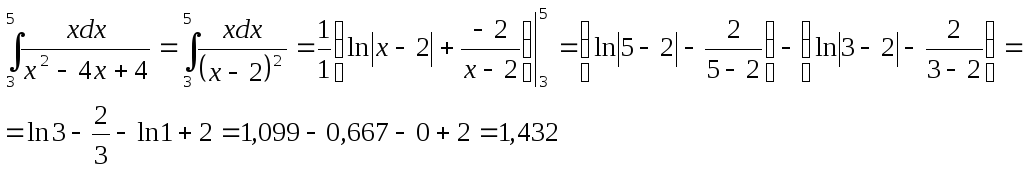
По табличному интегралу:

3.

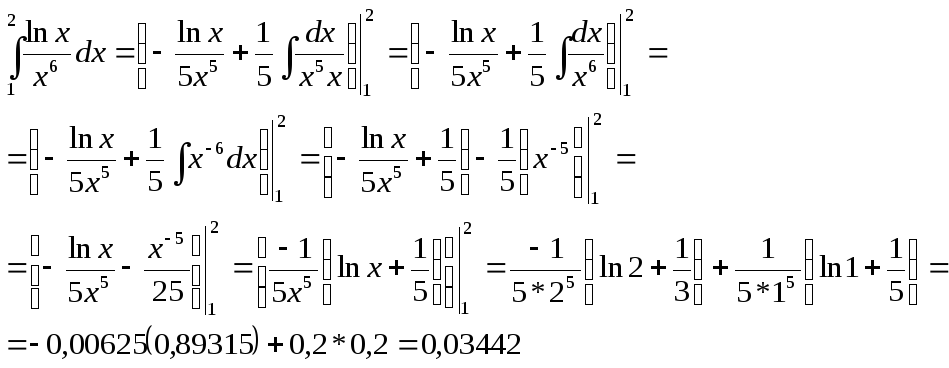
По табличному интегралу ; при .

4. - Это уравнение с разделяющимися переменными.

Делим обе части на и и разделяем:

;

.

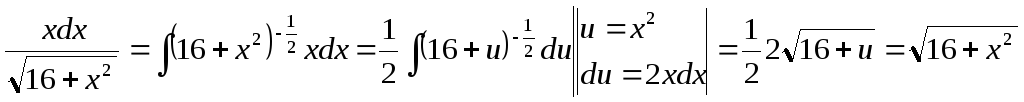
5. Графики функции ; ; .

Точки пересечения графиков:

и , точка (0;1)

и , точка (-1;2)

и , точка (-2;1)

Задача – найти площадь ABCD.

Найдем отдельно площади AECD, ABE, BCE.

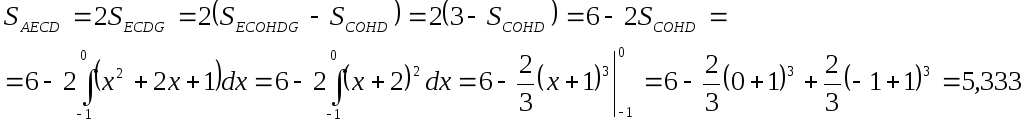
кв. ед.

кв.ед.

кв.ед.