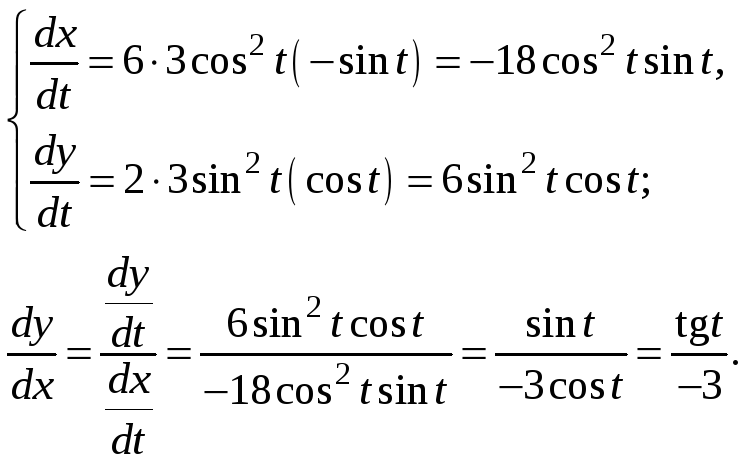Калинин / Приборостроителям / Математика 1 (12)

Задача 1

Доказать, что векторы образуют базис и найти координаты вектора в этом базисе:

Условие компланарности трёх векторов: .

Базис образуется векторами в том случае, когда они некомпланарны:

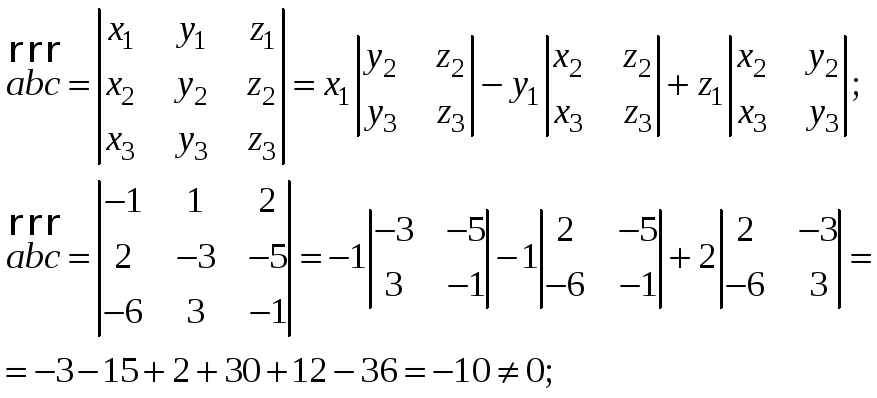
Данные три вектора образуют базис трёхмерного пространства.

Разложим вектор по элементам данного базиса (найдём компоненты А, В, С разложения вектора):

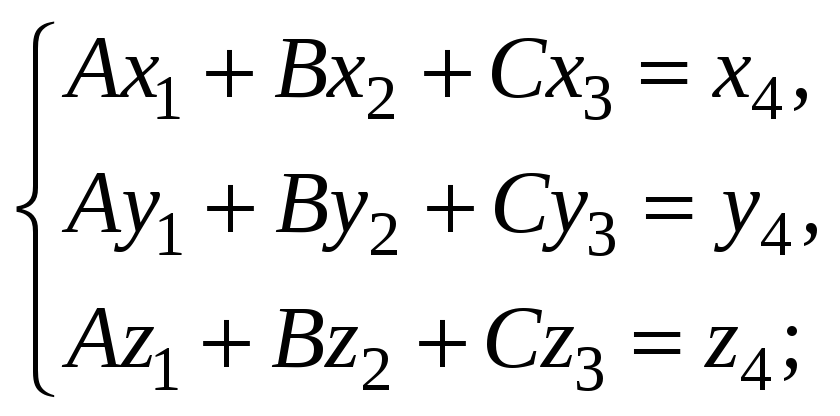
Подставляем значения и получаем систему из трёх уравнений с тремя неизвестными:

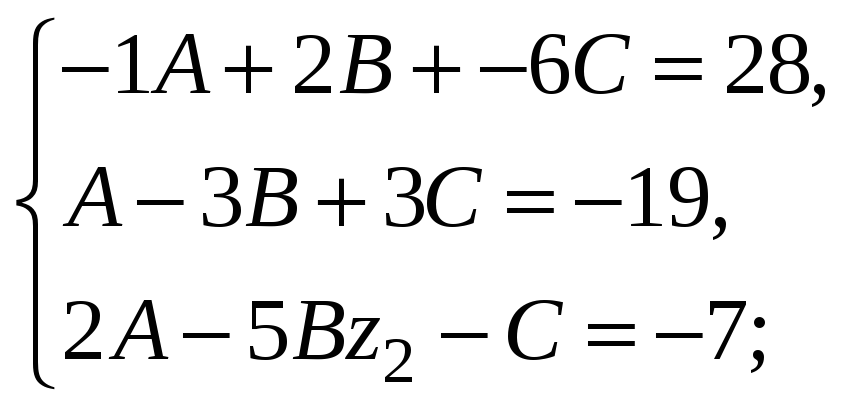
Решая её средствами Mathcad, получаем А=2; В=3; С=-4.

Таким образом разложение составит:

.

Задача 2

Даны четыре точки

Составить уравнения:

А) плоскости ;

Б) прямой ;

В) прямой , перпендикулярной плоскости ;

Г) прямой , параллельной прямой ;

Д) плоскости, проходящей через точку перпендикулярно к прямой .

Вычислить:

А) синус угла между прямой и плоскостью ;

Б) косинус угла между координатной плоскостью хОу и плоскостью .

1. Уравнение плоскости 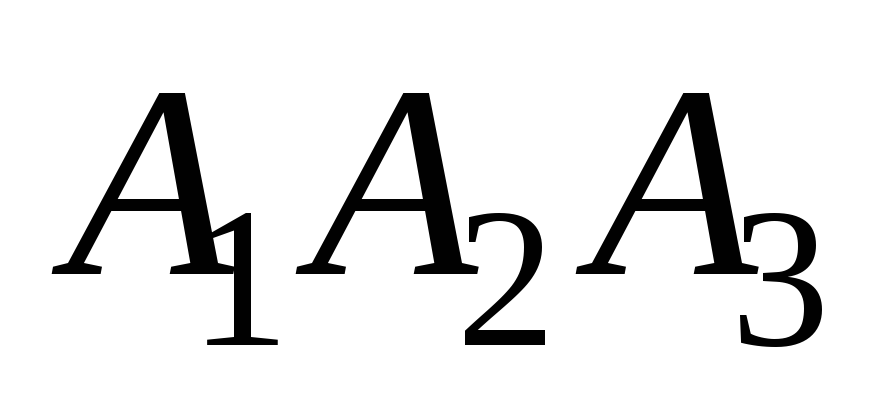имеет вид

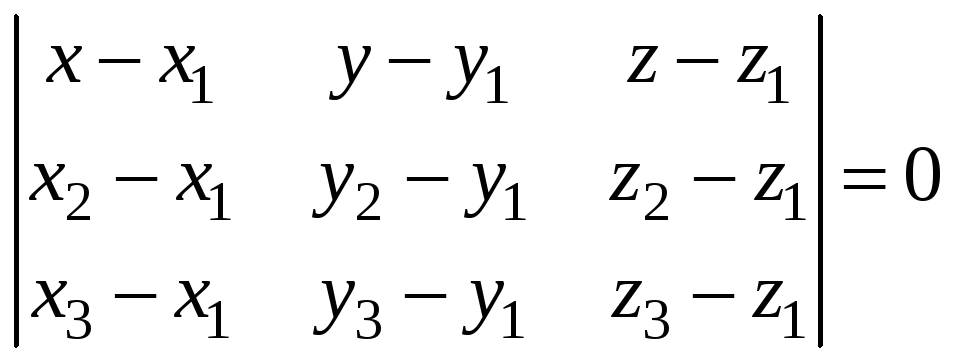
или для нашей задачи

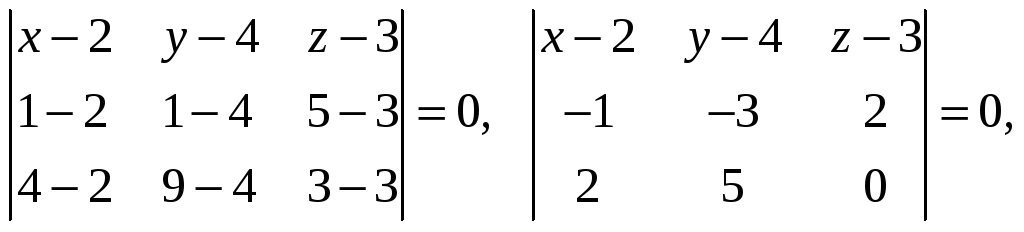
Разложим определитель по элементам первой строки:

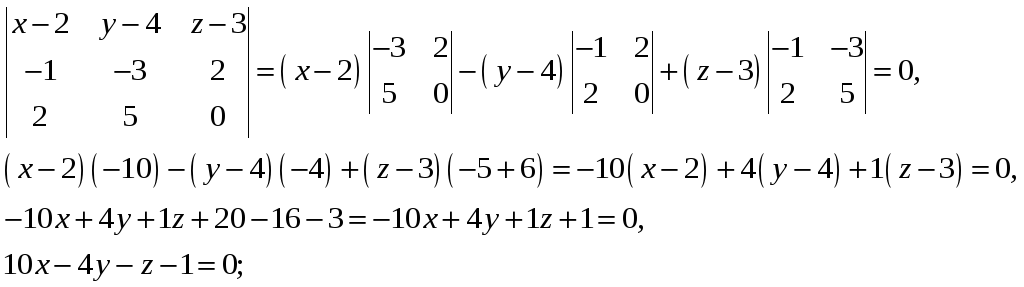
2. Уравнения прямо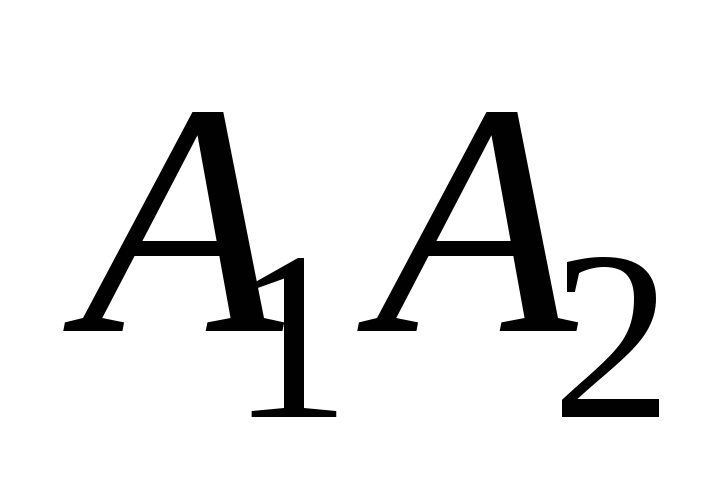й найдём в канонической форме, для этого воспользуемся уравнением прямой, проходящей через две заданные точки 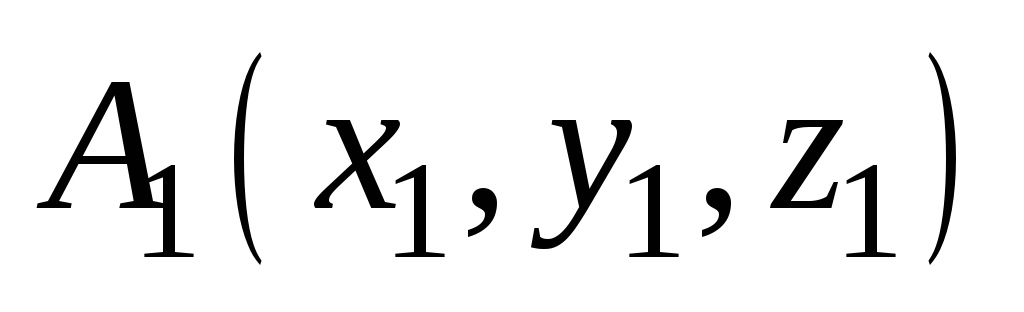и :

,

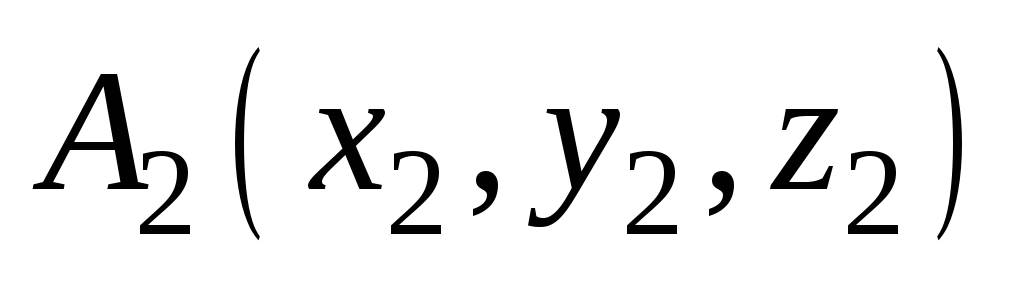3. Уравнения высоты, опущенной из вершины на грань 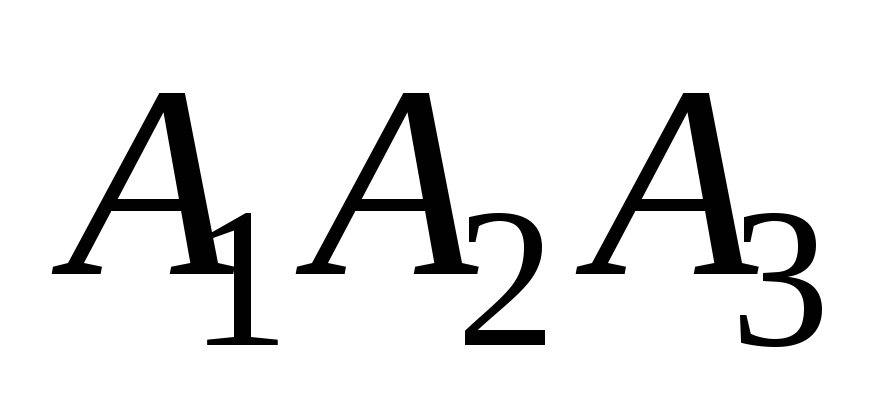(уравнение прямой , перпендикулярной к плоскости ).

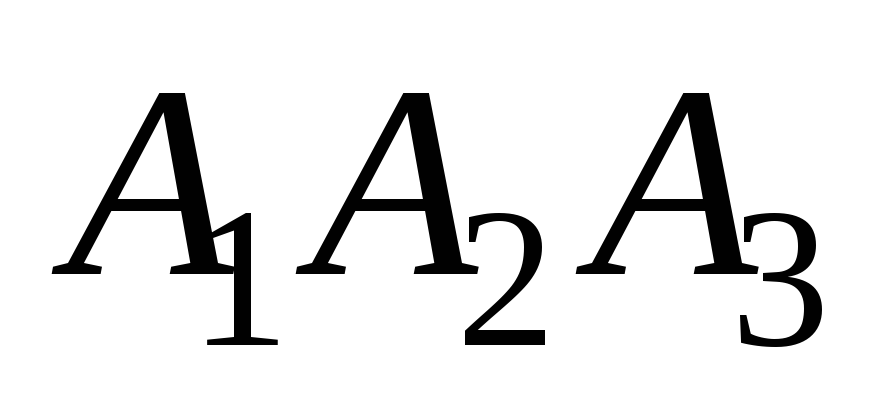Канонические уравнения прямой , проходящей через точку , имеют вид , где l, m, n – координаты направляющего вектора прямой.

Так как высота перпендикулярна плоскости , то из условия перпендикулярности прямой и плоскости координаты направляющего вектора прямой, перпендикулярной плоскости можно заменить координатами нормального вектора плоскости l=A=10; m=B=-4; n=C=-1.

Окончательно получим

4. Уравнение 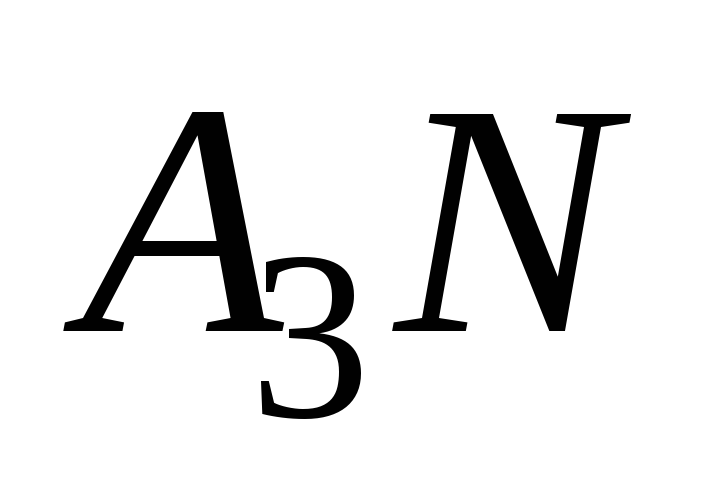прямой , параллельной прямой 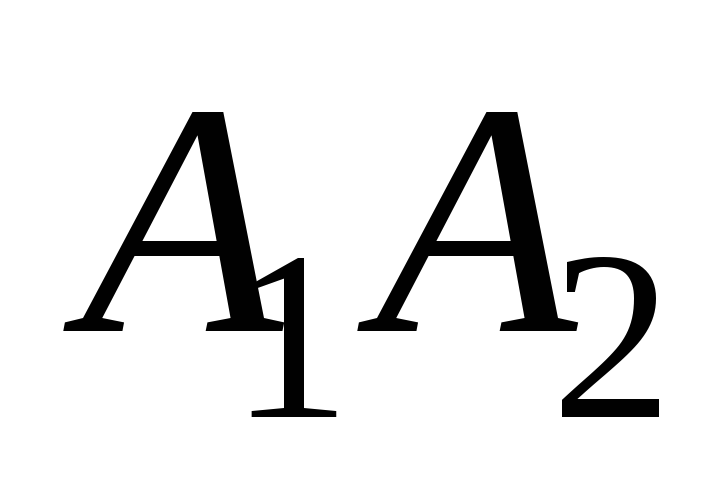будем искать в каноническом виде, учитывая, что для параллельных прямых 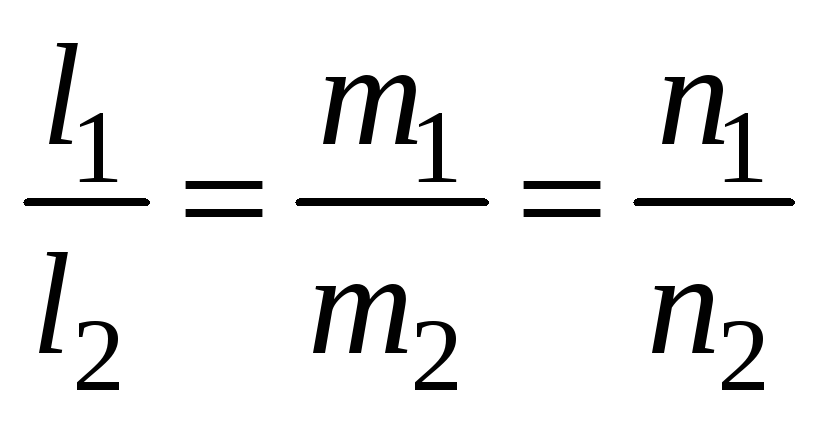. Тогда уравнение прямой, параллельной прямой 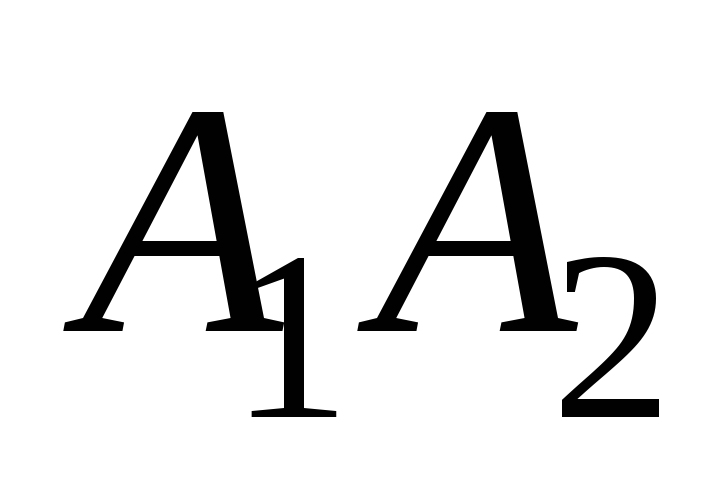и проходящей через точку :

5. Уравнение плоскости, проходящей через точку перпендикулярно к прямой найдём из соображений, что прямая принадлежащая данной плоскости так же как и плоскость, в которой она лежит параллельна и перпендикулярна другим геометрическим объектам.

Условие перпендикулярности двух прямых:

,

Откуда можно подобрать бесконечное множество прямых, перпендикулярных данной, например,

Теперь можно получить уравнение плоскости с данным направляющим вектором, проходящую через точку :

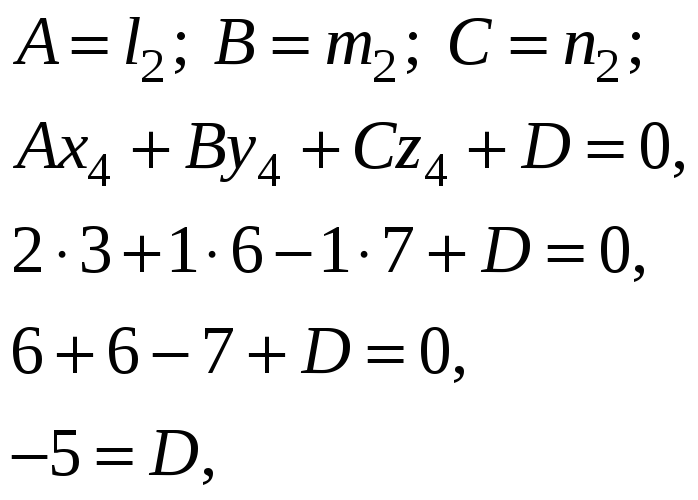
И окончательно, уравнение плоскости, проходящей через перпендикулярно прямой :

6. Углом ψ между ребром и гранью (плоскостью) будет острый угол между прямой 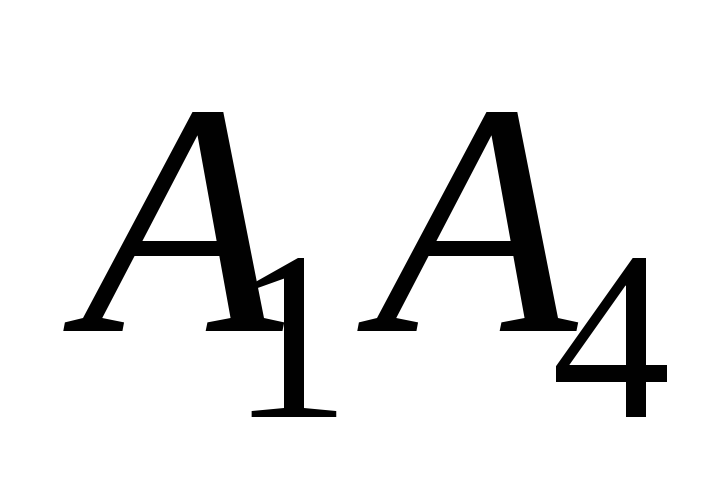и её проекцией на плоскость 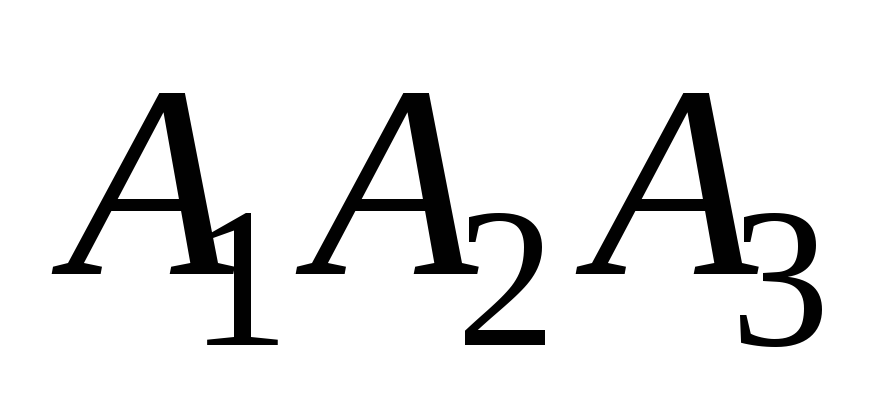. Для нахождения угла ψ воспользуемся формулой

Канонические уравнения прямой получим как:

Отсюда l=1; m=2; n=4, где l, m, n – координаты направляющего вектора прямой :

;

Уравнение плоскости было получено в пункте 5:

Отсюда А=10; В=-4; С=-1, где А, В, С – координаты нормального вектора плоскости :

Тогда получаем

7. Косинус угла между координатной плоскостью хОу и плоскостью :

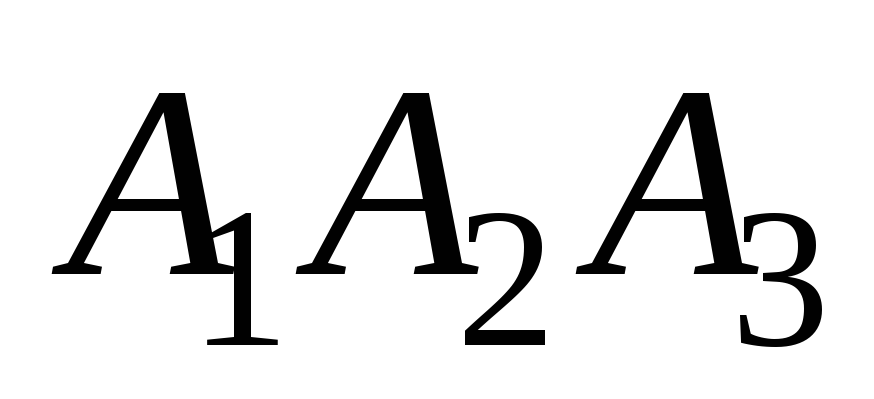Так как координатная плоскость хОу не имеет координаты z, то координатного числа n у плоскости не будет и, тогда уравнение косинуса угла между плоскостями найдём как угол между двумя прямыми, лежащими в этих плоскостях, причём прямая в плоскости хОу должна быть проекцией прямой из плоскости :

Задача 3

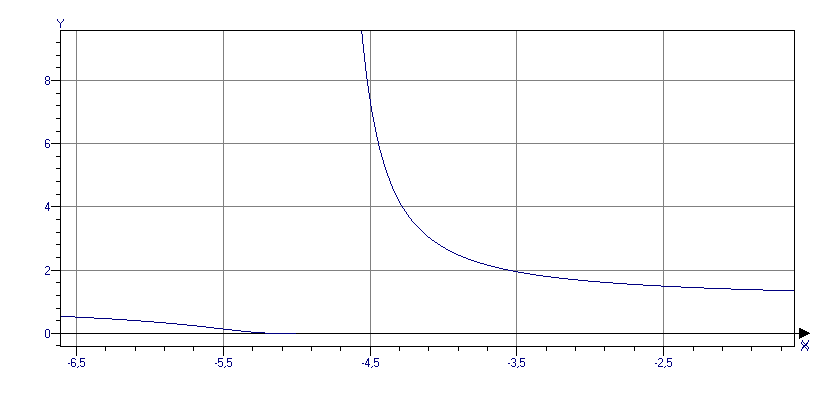
Провести полное исследование функций и построить графики

1. Область определения функции вся числовая прямая с выколотой точкой х=-5

2. Область значений функции всё множество положительных действительных чисел:

3. Функция всюду положительна (не имеет пересечений с осью абсцисс), с осью ординат пересекается в одной точке х=0

4. Функция имеет первую производную - функция монотонно убывает на всей области определения.

5. Функция имеет вторую производную 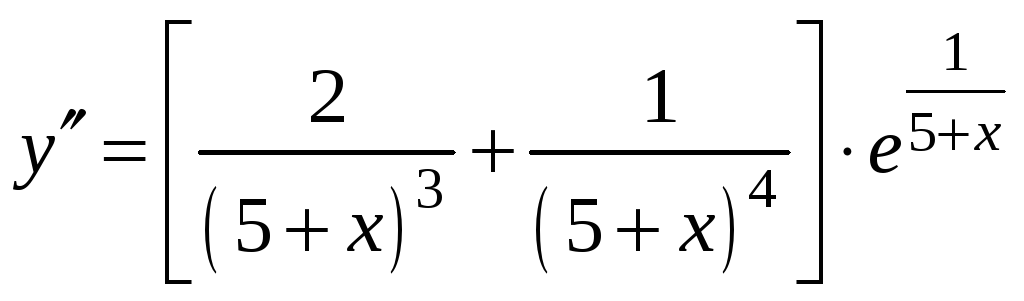- функция вогнута на всей области определения.

6. Функция имеет вертикальную асимптоту х=-5, горизонтальные асимптоты у=0 при стремлении х к бесконечности и .

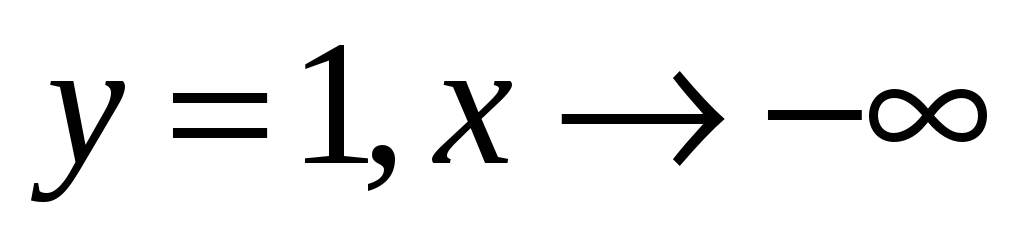7. Построение графика функции:

Задача 5

Даны вершины треугольника АВС: Найти:

А) уравнение стороны АВ,

Б) уравнение высоты СН,

В) уравнение медианы АМ,

Г) точку N пересечения медианы АМ и высоты СН,

Д) уравнение прямой, проходящей через вершину С параллельно стороне АВ,

Е) расстояние от точки С до прямой АВ.

1. Найдём уравнение стороны АВ. Найдём уравнение прямой, на которой лежит сторона АВ. Используем уравнение прямой, проходящей через две точки 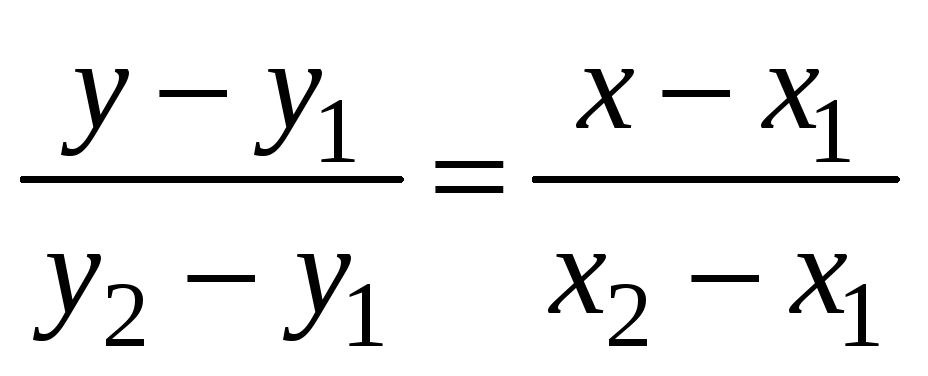, полагая

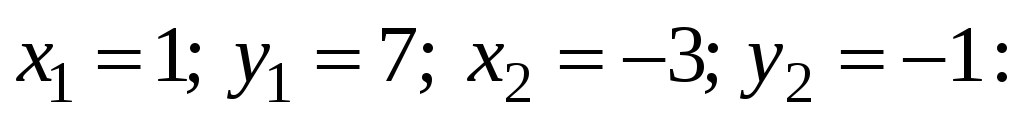
2. Найдём уравнение высоты, проведённой из вершины С. При составлении уравнения прямой, на которой лежит высота треугольника, воспользуемся формулой 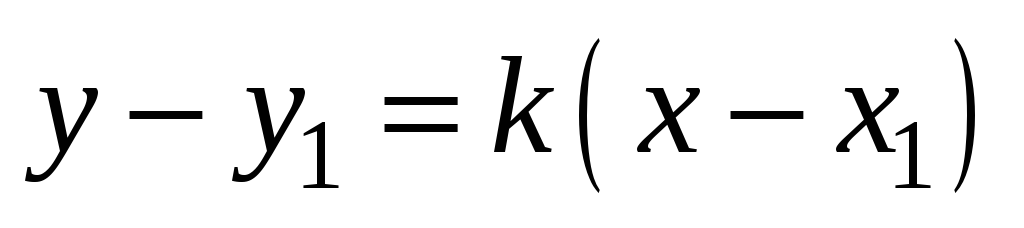и условием перпендикулярности двух прямых :

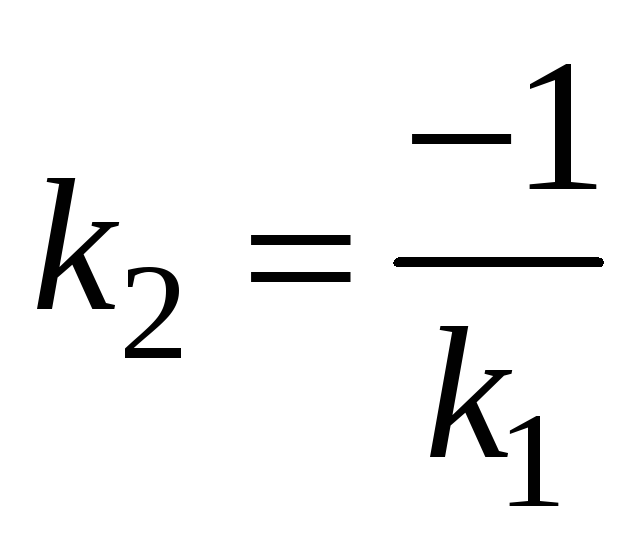Определим угловой коэффициент прямой АВ. Для этого разрешим уравнение стороны АВ относительно у:

Следовательно, высота, проведённая из точки С, имеет угловой коэффициент

Тогда, уравнение высоты, опущенной из вершины С(11;-3) на сторону ВС:

3. уравнение медианы АМ:

Медиана делит противолежащий высоте отрезок пополам, отсюда координаты точки М – середины отрезка ВС:

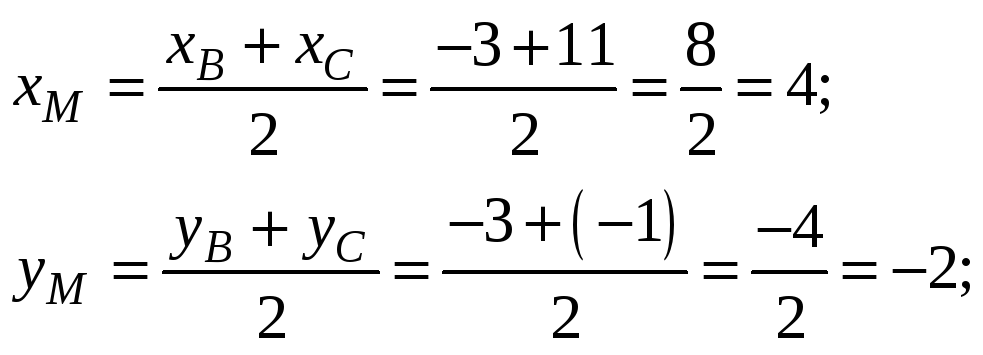
Уравнение медианы:

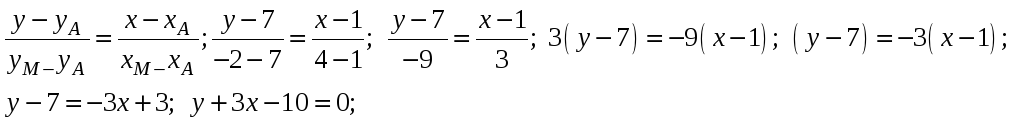
3. точку N пересечения медианы АМ и высоты СН:

Координаты пересечения двух прямых, заданных в общем виде:

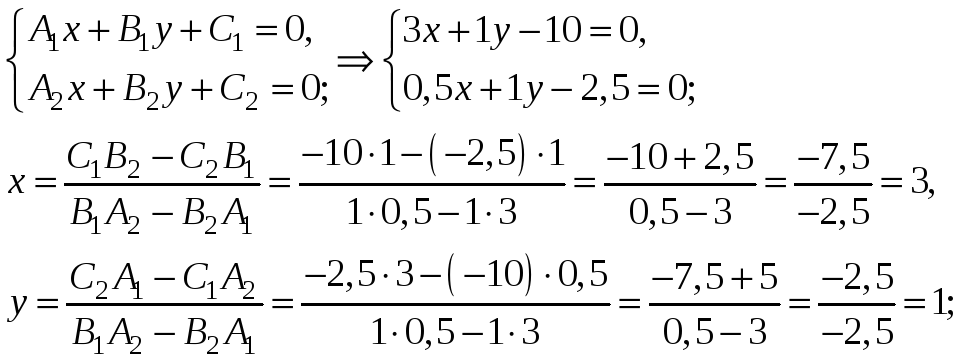
3. уравнение прямой, проходящей через вершину С параллельно стороне АВ

Прямая параллельна другой если имеет равный с той прямой угловой коэффициент k=2 для прямой АВ.

Уравнение прямой, проходящей через данную точку в заданном направлении:

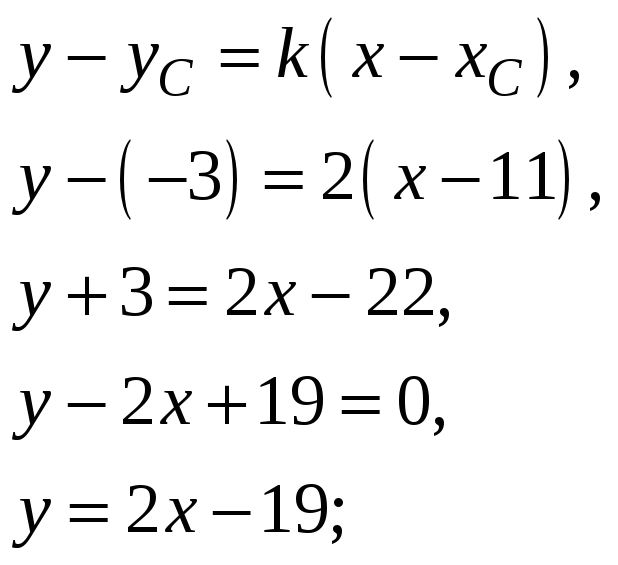
3. Найдём длину высоты, проведённой из вершины С. Она равна расстоянию от точки С(11;-3) до прямой АВ заданной уравнением 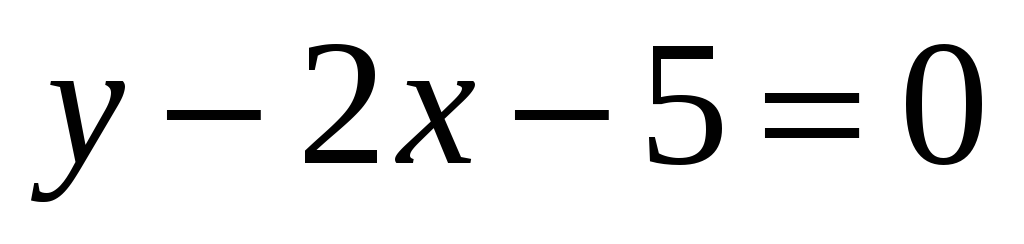. По формуле 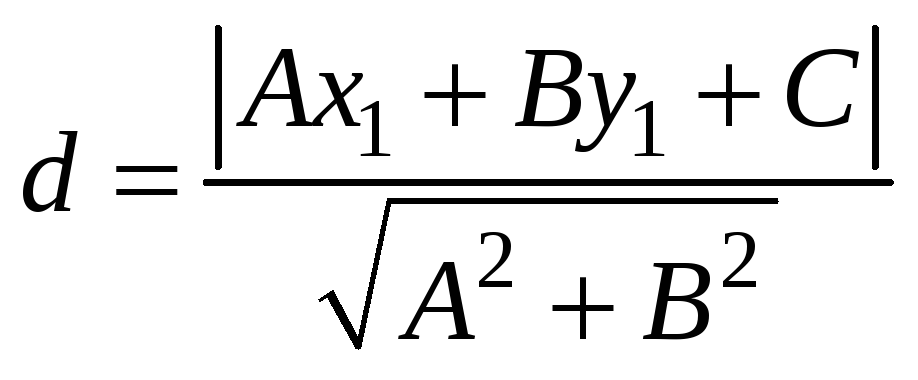вычисляем расстояние от точки А до прямой ВС, полагая

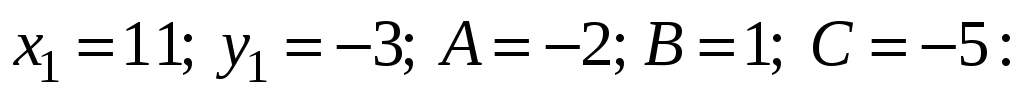
Задача 6

Проверить совместность системы уравнений и в случае совместности решить её:

А) по формулам Крамера;

Б) матричным методом;

В) методом Жордана-Гаусса.

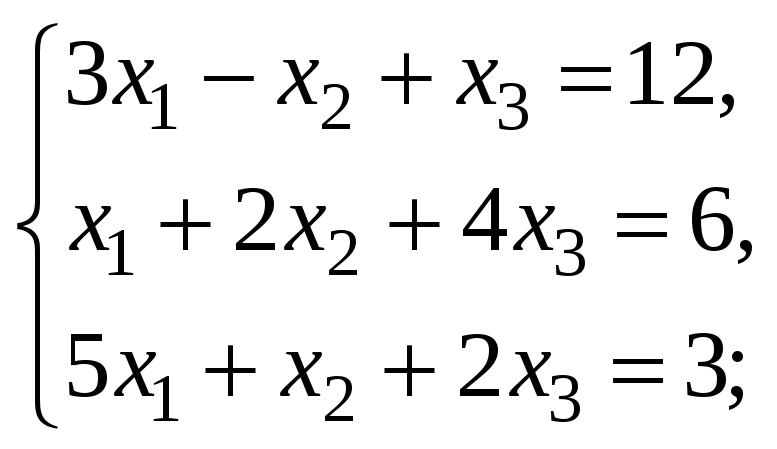
1. Метод Крамера

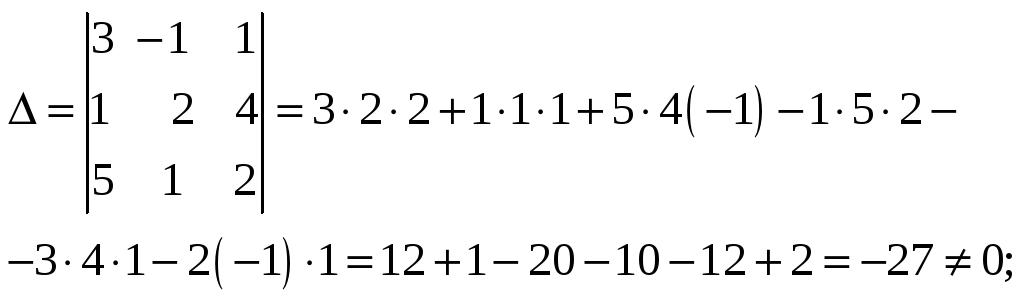
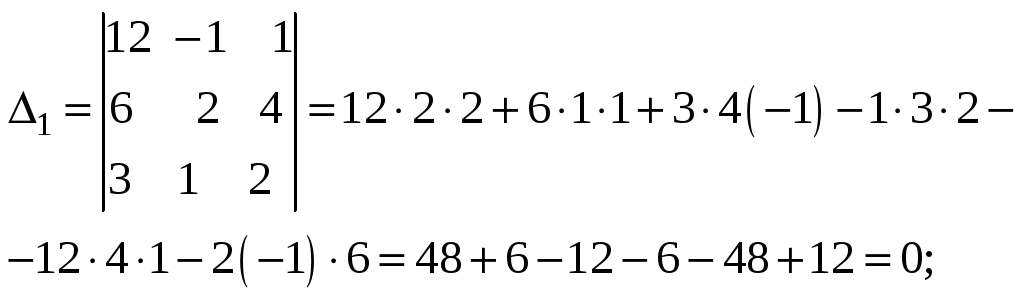
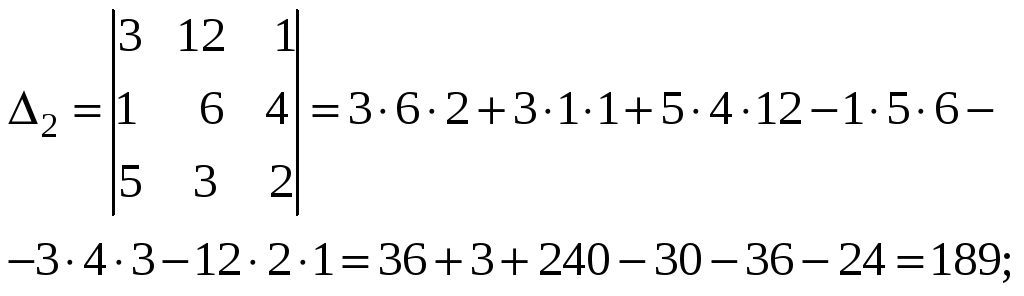
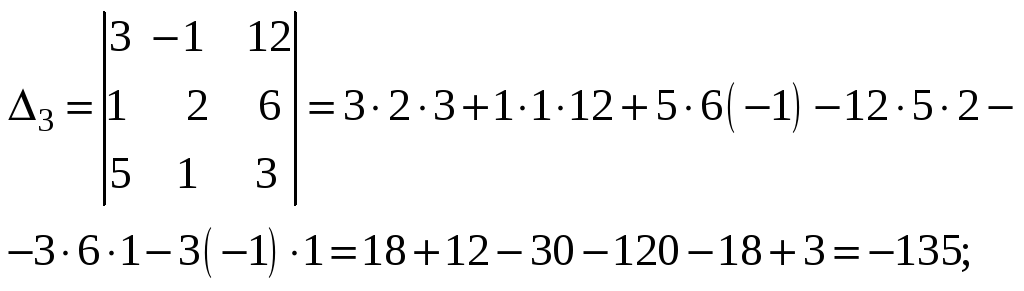
Отсюда

;

;

.

Проверка:

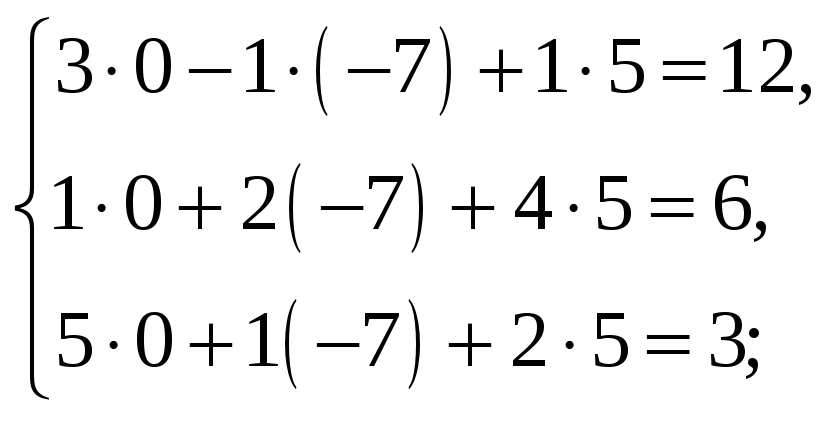
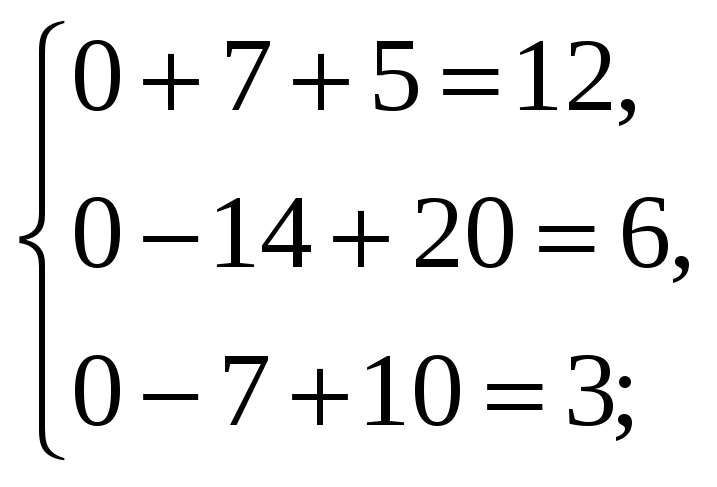
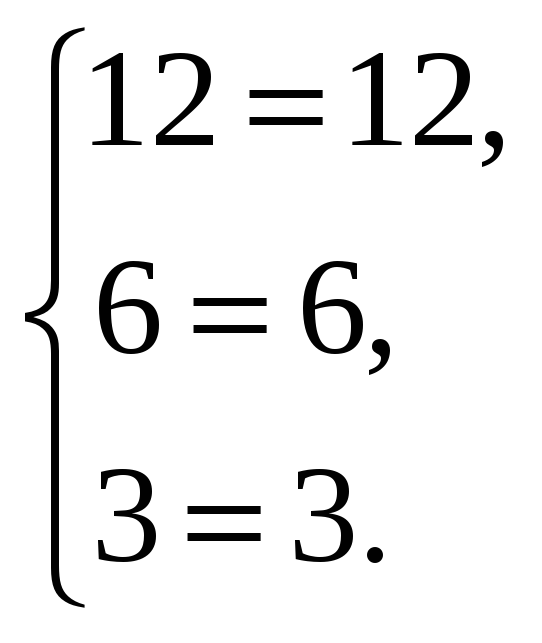
Уравнения системы превратились в верные тождества, что подтверждает правильность решения.

2. Метод обратной матрицы.

Главный определитель определили в предыдущем методе:

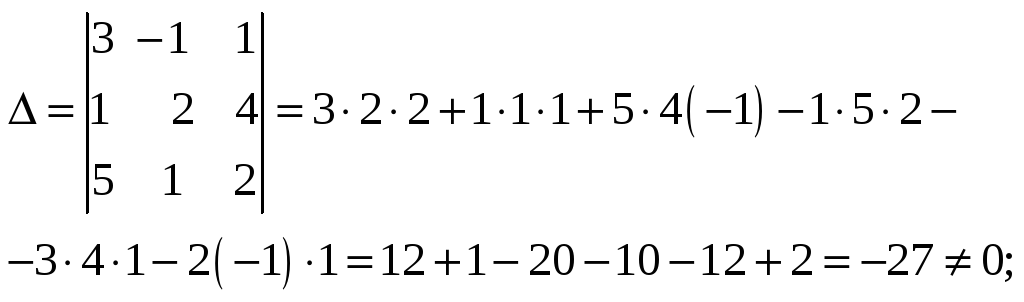
Вычислим алгебраические дополнения элементов этого определителя:

,

,

.

,

,

.

,

,

.

Тогда обратная матрица имеет вид

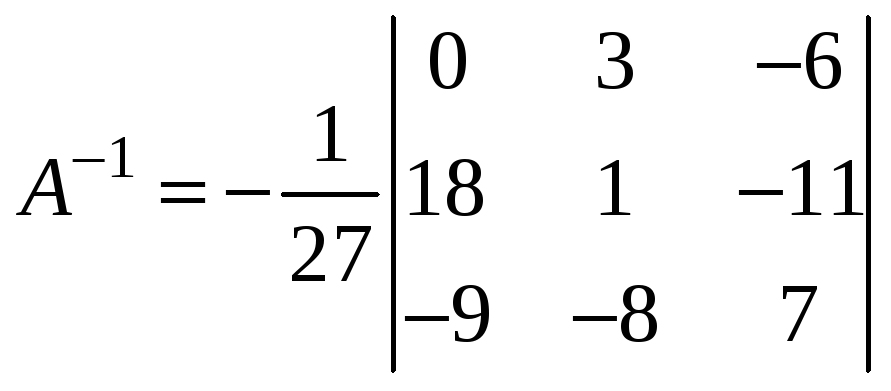
Следовательно

Следовательно:

;

;

. – что совпадает с предыдущим методом.

3. Метод Гаусса.

Составим расширенную матрицу системы и поменяем местами строки: первая станет второй, третья – первой, вторая – третьей. Затем вычтем из второй строки первую, умноженную на 3, а из третьей первую, умноженную на 5.

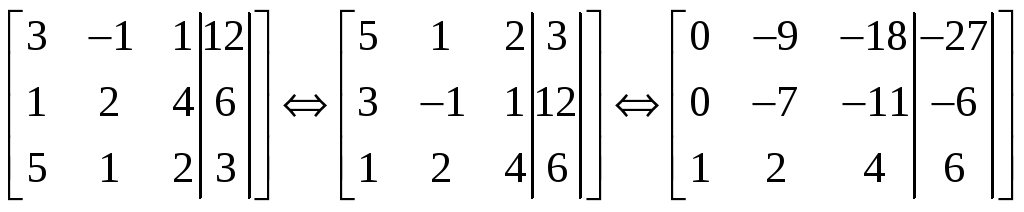
Затем преобразуем первую строку, поделив её на -9, и, умножив на -7, сложим со второй строкой, поделённой предварительно на -1:

Система уравнений приняла треугольный вид:

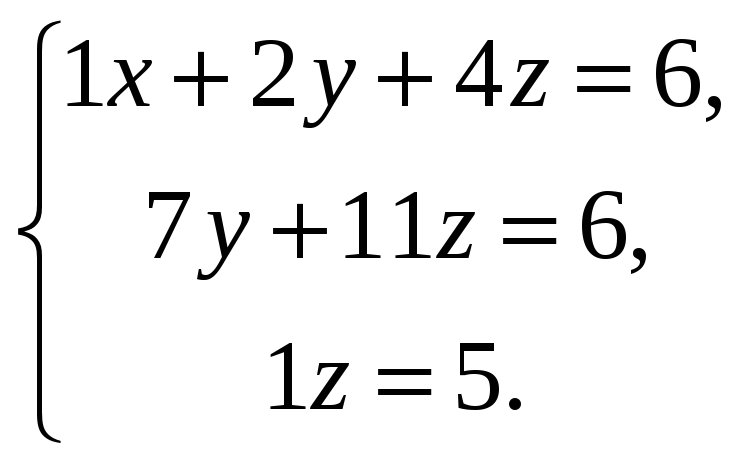Из последнего уравнения имеем .

Подставляя это значение во второе уравнение получаем .

Теперь из первого уравнения находим х.

.

;

;

.

Задача 7

Найти производную функции у

1)

2)

3)

4)

5)

1) Найдём производную непосредственным дифференцированием:

2) Найдём производную непосредственным дифференцированием как производную от произведения двух функций:

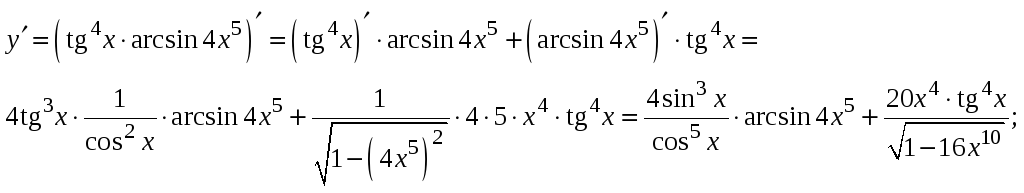
3) Найдём производную непосредственным дифференцированием как производную от частного двух функций:

4) Найдём производную дифференцированием данной функции как неявной:

5)

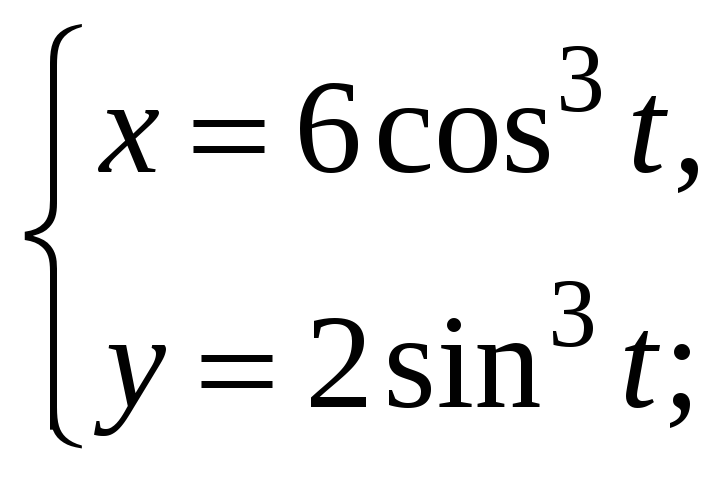
Находим :