Bilety / 18

18. Выпуклые функции. Признаки выпуклости функции. Необходимый признак точки перегиба, достаточный признак точки перегиба, их геометрический признак. Примеры

Выпуклые функции

     Функция f на интервале

     1) выпукла (выпукла вниз), если

     2) строго выпукла (строго выпукла вниз), если

     3) выпукла вверх, если

     4) строго выпукла вверх, если

     Признаки выпуклости дифференцируемых функций

     1. Если f' возрастает на , то f выпукла на (если f' строго возрастает, то f строго выпукла).

     2. Если , то f выпукла на (если обращаясь в нуль, возможно, лишь в конечном числе точек, то f строго выпукла).

     3. Функция f выпукла тогда и только тогда, когда график функции лежит не ниже касательной, проведенной к нему в любой его точке.

     Свойства выпуклых функций

1. 

В частности:

     2.

     3. Точки любой дуги графика лежат под хордой, стягивающей эту дугу.

     4. Функция f непрерывна на интервале и имеет в каждой его точке конечные односторонние производные.

     5. Функция f имеет на не более одного локального минимума и не имеет локальных максимумов.

     Точки перегиба

     Пусть функция f определена в некоторой окрестности точки x₀, непрерывна в точке x₀ и имеет в этой точке конечную или бесконечную производную. Если при переходе через точку x₀ функция f меняет направление выпуклости, то x₀ называют точкой перегиба функции f, а точку (x₀; f(x₀)) - точкой перегиба графика функции f. График функции переходит с одной стороны касательной, проведенной в точке (x₀; f(x₀)), на другую сторону. Точки перегиба f - точки экстремума для f'.

Необходимое условие перегиба.

Сформулируем необходимое условие перегиба графика функции.

Пусть график функции y=f(x) имеет перегиб в точке  и имеет при непрерывную вторую производную, тогда выполняется равенство .

Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения , в которых вторая производная равна нулю, являются абсциссами точек перегиба.

Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все  из области определения функции, для которых  и . Обычно это точки, в которых знаменатель первой производной обращается в ноль.

Первое достаточное условие перегиба.

После того как найдены все , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.

Пусть функция y=f(x) непрерывна в точке , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах этой окрестности слева и справа от , вторая производная имеет разные знаки, то  является точкой перегиба графика функции.

Как видите первое достаточное условие не требует существования второй производной в самой точке , но требует ее существование в окрестности точки .

Сейчас обобщим всю информацию в виде алгоритма.

Алгоритм нахождения точек перегиба функции.

Находим все абсциссы  возможных точек перегиба графика функции ( или  и ) и выясняем, проходя через какие  вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки  будут точками перегиба графика функции.

Второе достаточное условие перегиба.

Если , а , тогда  является абсциссой точки перегиба графика функцииy=f(x).

Пример.

Выяснить, является ли точка  точкой перегиба графика функции .

Решение.

Для начала убедимся, что точка  принадлежит графику функции:

Функция определена для всех действительных значений аргумента. Найдем первую и вторую производные.

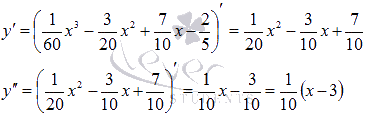
Вторая производная обращается в ноль при x=3, то есть необходимое условие перегиба графика функции в точке  выполнено, и эта точка может быть точкой перегиба. Воспользуемся вторым достаточным условием перегиба. Для этого найдем третью производную и убедимся, что ее значение при x=3 отлично от нуля.

Очевидно, что значение третьей производной отлично от нуля для любых x, в том числе и для x=3. Поэтому, по второму достаточному условию перегиба графика функции, точка  является точкой перегиба.