9. Кратные, криволинейные и поверхностные интегралы.
Векторный анализ.
371-380. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (a>0).
371.
372.
373.
374.
375.
376.
377.
378.
379.
380.
381-390. Вычислить с помощью тройного интеграла объём тела, ограниченной указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xOy.
381.
382.
383.
384.
385.
386.
387.
388.
389.
390.
391. Вычислить криволинейный интеграл.
вдоль дуги L окружности x=5cost, y=5sint, обходя её против хода часовой стрелки от точки A(5; 0) до точки B(0; 5). Сделать чертёж.
392. Вычислить криволинейный интеграл.
вдоль ломаной L=OAB, где O(0; 0), A(2; 0), B(4; 5). Сделать чертёж.
393. Вычислить криволинейный интеграл.
вдоль границы L треугольника ABC, обходя её против хода часовой стрелки, если A(1; 0), B(1; 1), C(0; 1). Сделать чертёж.
394. Вычислить криволинейный интеграл.
вдоль дуги L параболы y=x2 от точки A(-1; 1), до точки B(1; 1). Сделать чертёж.
395. Вычислить криволинейный интеграл.
вдоль верхней половины L эллипса x=3cost, y=2cost (0≤ t≤π). Сделать чертёж.
396. Вычислить криволинейный интеграл.
вдоль ломаной L=ABC, где A (1; 2),B (1; 5),C (3; 5). Сделать чертёж.
397. Вычислить криволинейный интеграл.
вдоль дуги L кривой y=e-x от точки A (0; 1) до точки B (-1; e). Сделать чертёж.
398. Вычислить криволинейный интеграл.
вдоль дуги L=AB прямой от точки A (1; 2) до точки B (2; 4). Сделать чертёж.
399. Вычислить криволинейный интеграл.
вдоль дуги L параболы y=2x2 от точки O (0; 0) до точки A (1; 2). Сделать чертёж.
400. Вычислить криволинейный интеграл.
вдоль дуги L кривой y=ln x от точки A(1; 0) до точки B (e; 1). Сделать чертёж.
401-410. Даны векторное поле F=Xi+Yj+Zk и плоскость Ax+By+Cz+D=0(p), которая совместно с координатными плоскостями образует пирамиду V. Пусть σ - основание пирамиды, принадлежащее плоскости (p); λ - контур, ограничивающий σ; n - нормаль к σ, направленная вне пирамиды V. Требуется вычислить,
1) поток векторного поля F через поверхность σ в направлении нормали n;
2) циркуляцию векторного поля F по замкнутому контуру λ непосредственно и применив теорему Скота к контуру λ и ограниченной им поверхности σ с нормалью n;
3) поток векторного F через полную поверхность пирамиды V в направлении внешней нормали к её поверхности непосредственно и применив теорему Остроградского. Сделать чертёж.
401.
402.
403.
404.
405.
406.
407.
408.
409.
410.
411-420. Проверить, является ли векторное поле F= Xi+Yj+Zk потенциальным и соленоидальным. В случае потенциальности поля F найти его потенциал.
411.
412.
413.
414.
415.
416.
417.
418.
419.
420.
10. Ряды
421-430. Исследовать
сходимость числового ряда
.
421.
422.
423.
424.
425.
426.
427.
428.
429.
430.
431-440. Найти интервал
сходимости степенного ряда
.
431.
. 432.
.
433.
. 434.
.
435.
. 436.
.
437.
. 438.
.
439.
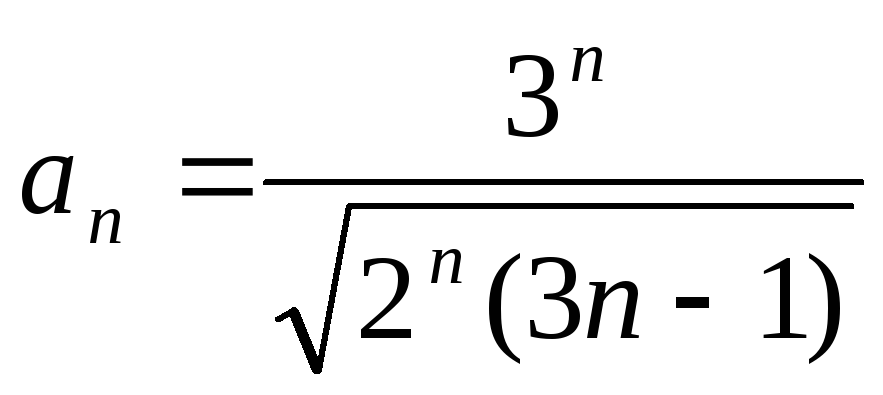. 440.
.
441-450. Вычислить
определённый интеграл
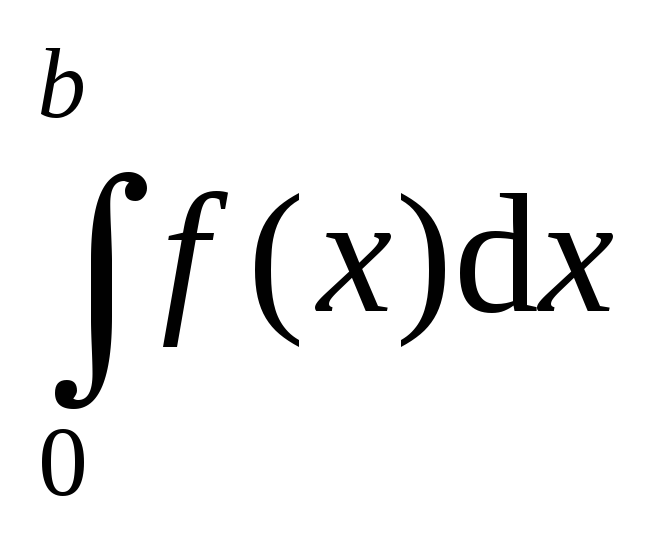с точностью до 0,001, разложив подынтегральную
функцию в степенной ряд и затем
проинтегрировать её почленно.
441.
442.
443.
444.
445.
446.
447.
448.
449.
450.
451-460. Найти три первых, отличных от нуля члена разложения в степенной ряд решения y=y(x) дифференциального уравнения y′=(x; y), удовлетворяющего начальному условию y(0)=y0,
451.
452.
453.
454.
455.
456.
457.
458.
459.
460.
461-470. Разложить данную функцию f(x) в ряд Фурье в интервале (a; b).
461.
в
интервале (-π; π).
462.
в
интервале (-2; 2).
463.
в
интервале (-π; π).
464.
в
интервале (-1; 1).
465.
в
интервале (-π; π).
466.
в
интервале (-2; 2).
467.
в
интервале (-π; π).
468.
в
интервале (-1; 1).
469.
в
интервале (-0; 2π).
470.
в
интервале (-π; π).