Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный экономический университет (бывш. ФИНЭК, ИНЖЭКОН)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МАТЕМАТИКА_КР2

.pdf

Скачиваний:

Добавлен:

14.03.2016

Размер:

1.58 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

10.

y tgx

cos2 x

11.

y ctgx

sin2 x

12.

y arcsin x

13.

y arccos x

1 x2

14.

y arctgx

1 x2

15.

y arcctgx

1 x

y f (x)

Логарифмической

производной

функции

называется производная от

логарифма этой

функции:

(ln y) y , при y > 0. Нахождение производных от многих y

функций значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. При этом логарифмическую производную применяют формально, не учитывая, что формула имеет смысл лишь при y > 0.

Функция y(x) называется неявной, если зависимость между х и у выражена уравнением F(x,y)=0, неразрешенным относительно у.

Чтобы найти производную от неявной функции, надо данное уравнение продифференцировать, считая у функцией от х, а затем полученное уравнение решить относительно производной y .

Рассмотрим примеры вычисления производных.

Пример 1. Найти производную функции y x3 3 . x 2 x 1

Решение. Применяя правила 4,1 и таблицу производных, получим:

3x 2 (x 2

x 1) (x3 3) (2x 1)

2x3

3x 2 6x 4

(x 2 x 1)2

(x2

1)2

Пример 2. Найти y

y 3cos

, если

(sin ( x)) .

Решение.

Последовательно

применяя

правило

дифференцирования сложной функции, получим:

y 3 2 cos(sin 5 (

)) cos(sin

5 (

))

6 cos(sin 5 (

))

( sin(sin 5				1		)))					1						))	6 cos(sin 5 (							1		)) sin(sin 5						1		))
				(							(sin 5 (																						(
				(	x						(sin 5 (					x										x							(	x
1						1												1										1
5sin 4 (			)	(sin(						)) 30 cos(sin 5 (													)) sin(sin 5 (								))
5sin 4 (		x	)	(sin(					x	)) 30 cos(sin 5 (										x			)) sin(sin 5 (						x		))
1						1					1							1										1
sin 4 (		) cos(						)			(			) 30 cos(sin 5 (										)) sin(sin 5				(				))
sin 4 (	x	) cos(					x	)			(		x	) 30 cos(sin 5 (							x			)) sin(sin 5				(		x		))
sin 4 (	1	) cos(					1	)				1			.
sin 4 (		) cos(						)							.
	x						x					x 2
Пример 3. Найти производную функции y (x 3)sin 2x .
Решение. Применим логарифмическую производную:
				ln y ln( x 3)sin 2x														sin 2x ln( x 3)
				y		2 cos 2x ln( x 3)													sin 2x
				y															sin 2x
				y															x 3
				y															x 3
																						sin 2x
				y y 2 cos2x ln( x 3)
				y y 2 cos2x ln( x 3)
																								x 3

	y (x 3)		sin 2x			sin 2x
			2 cos2x ln( x 3)				.

						x 3
	Пример4.	Найти			производную		функции
y	e x2 sin 3 (x 4) arctg (x3 )			.
	tg 4	(x 1)

	Решение.	В	случае		произведения		нескольких
сомножителей		применение			логарифмической		производной

также эффективно:

ln y ln e x2 ln sin 3 (x 4) ln arctg (x3 ) ln tg 4 (x 1)

3ln sin( x 4) ln arctg (x3 ) 4 ln tg(x 1).

cos(x 4)

3x2

2x 3

arctg (x3 ) 1 x6

sin( x 4)

tg(x 1) cos2 (x 1)

e x2

sin 3 (x 4) arctg (x3 )

tg 4 (x 1)

cos(x 4)

3x2

sin( x 4)

) 1 x

arctg(x

tg(x 1) cos

Пример

5. Найти

производную функции

y(x) ,

если

x 2 3xy 2

2 y 1

x 2 y

Решение. Применим правило дифференцирования

неявной функции:

2x 3 1 y 2 x 2 y y

2 y

(2x y )(2 y

(x 2 y) 2

2 y

y) 2x(2 y

2x 3y 2

6xyy

1) y (2 y 1)

(x 2 y) 2

2 y 2 y 1) 2x(2 y 1)

2x 3 y 2

6xyy

y (2x

(x 2 y) 2

2x(2 y 1)

y (2x

2x 3 y

( x 2

y) 2

( x 2 y) 2

6xyy

(2x 2

2x(2 y 1)

2 2x 3y

6xy

2x(2 y 1) (2x 3y 2 )( x 2 y) 2

(2x 2 1 6xy(x 2 y) 2 )

КОНТРОЛЬНЫЕ ЗАДАНИЯ

Найти производные функций, заданных в явном и неявном виде.

2.1.

a) y 5 arcsin 2

3 1 5x2 ;

b) x 2 3xy

y3 2

2.2.

a) y 5 3x cos x ;

b) y x xy

a) y

3 y

2.3.

; b) x3 y xy 3 e 2 .

tg 4

5x3

3 6x

1 x

2.4.

a) y

;

b) yx 2 xy 3 ln(x 2

y 2 ).

		lg(x 1) tg 2	(2x) e x3
2.5.	a) y			b) x3	y2 x2	sin( xy).
		(x2	1)3

2.6.a)

2.7.a)

2.8.a)

2.9.a)

2.10.a)

xy2 3

y 4 cos

arcctg (x

3x) ; b)

xy 4

sin 2x

xy x y 2 .

y 1

b) xy arcctg 2

x3 3x2 1

; b) y 2 x

e3 y2

5y.

3 1 sin 2x

xy 2 4x

(arcsin 3x) 3

; b)

6x.

2 x2 arctg 2 x ln(x 2 1)

; b) y

xy 5

sin 3 x

2.11. a) y sin 3 (x			1		); b) 2x3	3y		xy 3		.

			e3x					xy 4
		x 3 x2					3x 2 2
2.12.	a) y ctg			; b) xy 10 y 2					.
							2 y 5
		2

y 2 x

2.13. a) y 3

; b)

x 2 y3 .

x y

x 1

2 x2

2.14.

a) y 1

; b) x3 y xy 3 sin( xy).

x 1


2.15.	a) y	x3	2 ln5 (2x 3)	; b) cos y	x 2 y 1	.
					x y3
			3 arcsin x
			3 arcsin x

2.16.a) y 3ln 4 (arcsin 2 x);

2 arcsin (

2.17.a) y arctg(x )


	3		2x2 1
2.18.	a) y			;	b)
2.18.	a) y	sin 2 x 1		;	b)
		sin 2 x 1
2.19.	a) y (ln x)lg3 x ;				b)

b)		y 2		xy sin y 1.
b)		x3		xy sin y 1.
		x3
x2 ) ; b) xy					x	cos2 y .
x2 ) ; b) xy					y	cos2 y .
					y
							x
	x2 y 2 x					2 y	x	.
	x2 y 2 x					2 y		.
							y
x 2 1			x3 y 2 .

y 2 1
y 2 1

2.20.

a) y

3x2

2 x3

; b)

ln3 x

ln 2 (x 1)

sin y

УКАЗАНИЯ К ЗАДАНИЮ 3.

ТЕМА 3. ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА

Внутренняя точка x0 интервала (a,b) называется точкой

максимума (минимума) функции	f (x) , если существует
такое 0 , что для всех x из	интервала (x0 , x0 ) ,

содержащегося внутри интервала (a,b) , выполняется

неравенство f ( x0 ) f ( x) ( f ( x0 ) f ( x)). Точки максимума и минимума называют точками экстремума (локального экстремума) функции. Точки, в которых производная обращается в ноль, называют стационарными точками.

Приведем формулировки теорем, используемых при исследовании функций.

Достаточное условие строгого возрастания (убывания)

функции.
Если			(a,b) , то	f (x)
	f (x) 0	( f (x) 0) в интервале

строго возрастает (убывает) в этом интервале.

Промежутки, в которых функция возрастает (убывает),

называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции необходимо:

1.найти область определения функции;

2.найти производную функции;

3. приравнять производную к нулю и определить ее корни (стационарные точки), а также найти точки, в которых производная не существует, а функция определена;

4. определить знак производной в каждом из промежутков, на которые разбивается полученными точками область определения функции.

Необходимое условие экстремума функции

Если функция f (x) дифференцируема в точке x0 и достигает в этой точке максимума (минимума), то f (x0 ) 0.

Точками экстремума могут быть только те точки, в которых производная равна нулю, либо не существует. Точки, в которых производная равна нулю или не существует, называют точками, подозрительными на экстремум, или критическими точками.

Достаточные условия экстремума функции

Если при переходе через точку x0 , подозрительную на экстремум, производная меняет знак, то точка x0 является точкой экстремума. При этом если в некоторой окрестности

точки x0	f			x x0		и f			для x x0 , то x0
		(x) 0 для					(x) 0
является	точкой максимума.					Если	же в		этой	окрестности
	для		x x0 и		0 для			x x0 , то		x0	– точка
f (x) 0				f (x)
минимума.
Другим			достаточным			признаком			существования
экстремума		в	стационарной			точке		x0	является		условие

		(тогда
f (x0 ) 0 (тогда это точка максимума) и	f (x0 ) 0	(тогда
это точка минимума). При этом считается,	что f (x)	имеет

непрерывную вторую производную в некоторой окрестности

точки x0 .

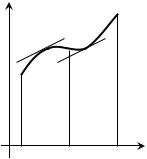
График функции y f (x) называется выпуклым (или выпуклым вверх) в интервале (a,с) , если он расположен не выше касательной проведенной в любой точке этого интервала (рис.1).

График функции y f (x) называется вогнутым (или выпуклым вниз) в интервале (с,b) , если он расположен не ниже касательной, проведенной в любой точке этого интервала (рис. 1).

y =f(x)

0 a

b X

Рис. 1

Достаточные условия выпуклости (вогнутости) графика функции

Если f (x) 0 в интервале (a,b), то график функции является выпуклым в этом интервале; если же f (x) 0, то в интервале (a,b) график функции вогнутый.

Точка x0 ; f (x0 ) графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.

Если x0	─ абсцисса	точки перегиба графика		функции
y f (x),	то вторая	производная равна	нулю	или	не
существует в этой точке. Точки, в которых					или
			f (x) 0

f (x) не существует, называются критическими точками второго рода.

Если при переходе через критическую точку второго рода x0 вторая производная меняет знак, то точка x0 ; f (x0 ) есть

точка перегиба.

Прямая l называется асимптотой кривой y = f(x), если расстояние точки М(х,у) на кривой от прямой l стремится к нулю при неограниченном удалении этой точки по кривой от начала координат, (т.е. при стремлении хотя бы одной из

координат точки к бесконечности).

Прямая

y a

является

вертикальной

асимптотой

кривой y = f(x), если:

lim

f ( x)

или

lim f (x) .

x a 0

Прямая

y b

является

горизонтальной

асимптотой

кривой y

= f

(x),

если

существует

lim f (x) b

или

lim f (x) b .

y kx b

Прямая

является

наклонной

асимптотой

кривой y = f(x), если существуют пределы:

k lim

f (x)

, b lim( f (x) kx),

или

k lim

f (x)

, b lim ( f (x) kx) .

При исследовании функции и построении ее графика удобно придерживаться следующего плана.

1.Найти область определения функции.

2.Определить четность (нечетность), периодичность функции.

3.Найти точки разрыва.

4.Определить точки пересечения графика с осями координат.

5.Найти точки экстремума и вычислить значения функции в этих точках.

6.Определить интервалы возрастания и убывания функции.

7.Найти точки перегиба, интервалы выпуклости и вогнутости.

8.Определить асимптоты.

9.Найти предельные значения функции при аргументе,

стремящемся к границам области определения.

В процессе исследования функции не обязательно строго придерживаться приведенной схемы.

Пример. Исследовать функцию	f (x)	x 2	и построить ее
		x
	1
график.

Решение.

1. Данная функция определена и непрерывна на всей оси ОХ, за исключением точки x 1, где она терпит бесконечный разрыв. Область определения функции

х ( ; 1) ( 1; )
2.	Поскольку	f ( x) f (x) и	f ( x) f (x) , то

рассматриваемая функция не является ни четной, ни нечетной, то есть это функция общего вида. Функция непериодична.

3.Точка х=-1 является точкой разрыва.

4.Точка (0;0) является точкой пересечения функции с осями координат.

5.Точки экстремума.

Вычислим производную:

y /	2x(1 x) x2	x2 2x	x(x 2)		.
	(1 x)2	(1 x)2	(1	x)2

Производная обращается в нуль при x 0						и x 2.
Производная не существует при х=-1.

Точка ( 2; 4) ─максимум, а точка (0,0) ─минимум функции.

Построим интервалы монотонности (рис. 2):

Y '(x) +	-	-	+	x
				x
Y (x)	-2	-1	0
	-2	-1	0

Рис. 2

6.Функция возрастает при x ( ; 2) (0; )и убывает при x ( 2; 1) ( 1;0) .

7.Найдем вторую производную:

y"		(2x 2) (1 x)2		2(1 x) (x2		2x)
			(1	x)4

	2x 2 2x2		2x 2x2 4x			2	.
			x)3			x)3
		(1			(1
	Вторая производная в нуль нигде не обращается, но при

переходе через точку x 1 меняет свой знак с минуса на плюс. Следовательно, в интервале ( ; 1) график функции выпуклый, а в интервале ( 1; ) ─ вогнутый. Точек перегиба функция не имеет.

8. Асимптоты функции.

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.04.20192.44 Mб5Матем (ПОСОБИЕ). doc моё.doc
#
01.04.2015150.45 Кб24матем.docx
#
01.04.20151.97 Mб18Математика Лин алгебра КР 2012.doc
#
20.08.20191.77 Mб1Математика(1).doc
#
10.12.20181.77 Mб4математика.doc
#
14.03.20161.58 Mб11МАТЕМАТИКА_КР2.pdf
#
02.04.2015575.63 Кб12Математические метод.pdf
#
16.11.2019139.78 Кб5Матер к зан.07.09.doc
#
25.11.2019132.49 Кб5Материал для распечатки к 101112.docx
#
22.12.2018338.94 Кб8Материал для студентов.doc
#
01.04.2015537.6 Кб30Материаловедение.doc