10

ЛАБОРАТОРНАЯ РАБОТА № 4

Спектральный анализ сигналов с угловой модуляцией

Цель работы. Изучение спектрального состава сигналов с частотной и фазовой модуляцией при изменении параметров несущего и модулирующего сигналов.

I. Теоретическая часть Введение

С целью снижения уровня помех при приеме радиосигналов в радиотехнике используется сигналы с угловой модуляцией. Изменение частоты или фазы высокочастотного (ВЧ) сигнала по закону передаваемого сообщения называется угловой модуляцией. Природные помехи, в основном, имеют вид амплитудно-модулированных (АМ) сигналов. Поэтому применение сигналов с угловой модуляцией значительно снижает уровень помех и повышает качество передачи, но за это приходится платить значительным усложнением конструкции передатчика и расширением полосы занимаемых частот (примерно в 56 раз по сравнению с АМ-сигналом).

1. Радиосигналы с угловой модуляцией

Изменение частоты по закону передаваемого сообщения называется частотной модуляцией (ЧМ), изменение начальной фазы по закону передаваемого сообщения – фазовой модуляцией (ФМ). Поскольку в обоих случаях аргумент гармонического колебания определяет мгновенное значение угла, то такие радиосигналы имеют общее название – сигналы сугловой модуляцией (УМ).

2. Частотно-модулированные сигналы

Изменение несущей частоты ВЧ гармонического сигналапо закону передаваемого сообщения называетсячастотной модуляцией (ЧМ), где  амплитуда,  частота,  начальная фаза ВЧ-сигнала. В радиотехнике ВЧ-сигнал принято называть несущим,  несущей частотой,  амплитудой несущего сигнала. При ЧМ несущая частота зависит от модулирующего сигнала как

, (1)

k – коэффициент пропорциональности, размерность которого определяется размерностью модулирующего сигнала. Рассмотрим случай однотональной модуляции. Это означает, что модулирующий сигнал является гармоническим , где– частота модулирующего сигнала. В этом случае мгновенная частота ЧМ-колебания равна:

, (2)

где величину принято называтьдевиацией частоты несущего сигнала. Девиация частоты – максимальное отклонение частоты ВЧ-сигнала при ЧМ от частоты несущего колебания . Полную фазу ЧМ-колебания в любой момент времени определим путем интегрирования

. (3)

Величину , которая являетсядевиацией фазы, принято называть индексом угловой модуляции при ЧМ:

. (4)

Из соотношения (3) следует, что при частотной модуляции происходит и фазовая модуляция. С учетом соотношения (3) выражение для ЧМ-сигнала запишется в виде:

. (5)

На рис.1 представлены временные осциллограммы соответственно несущего колебания (а), модулирующего (б) колебания и ЧМ-сигнала (в).

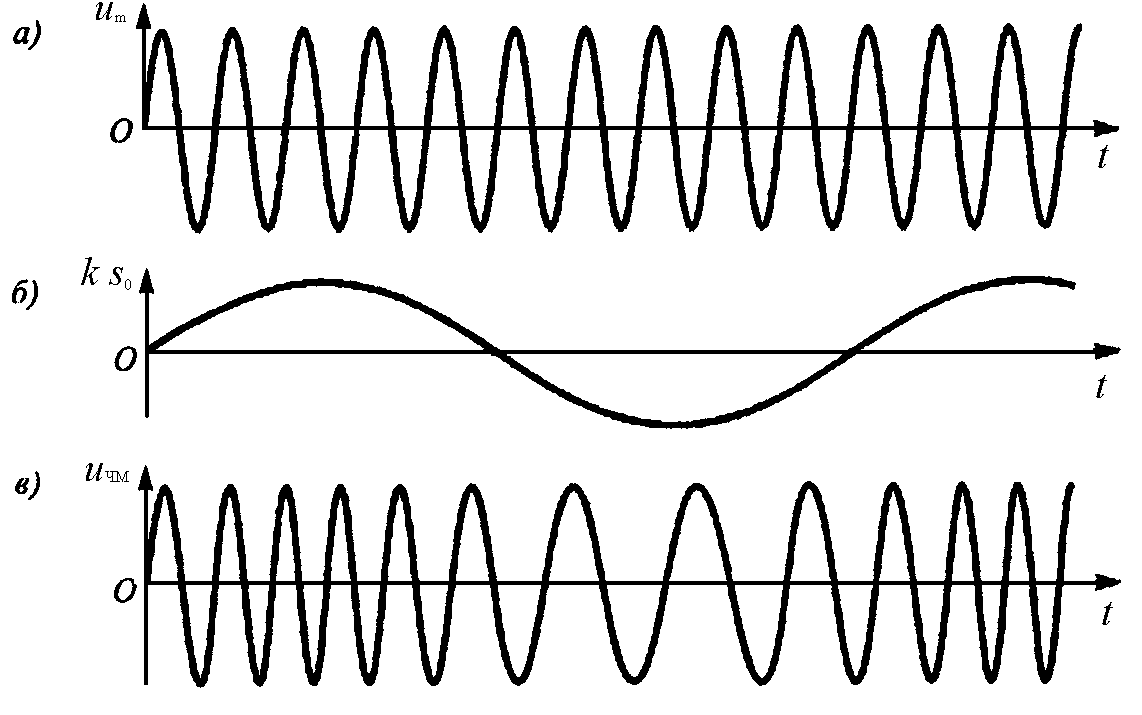
Рис. 1. Частотная однотональная модуляция: а) несущее колебание,

б) модулирующий сигнал, в) ЧМ-сигнал

3. Спектр частотно-модулированного сигнала при однотональной модуляции

Используя тригонометрическое соотношение выражение для ЧМ-сигнала запишется в виде:

. (6)

Проведем анализ полученного выражения.

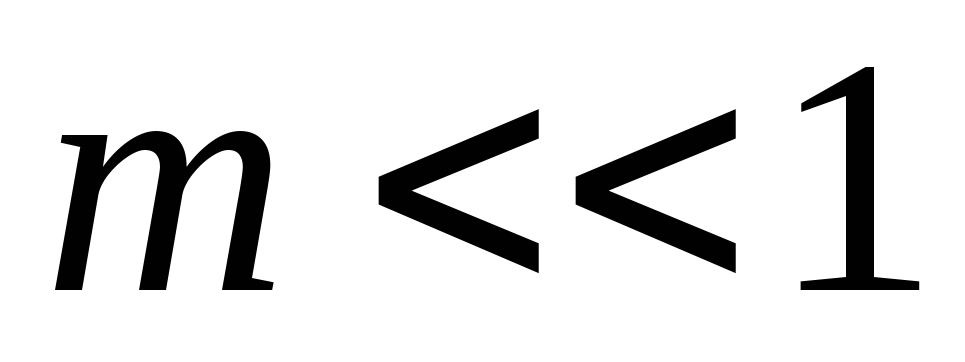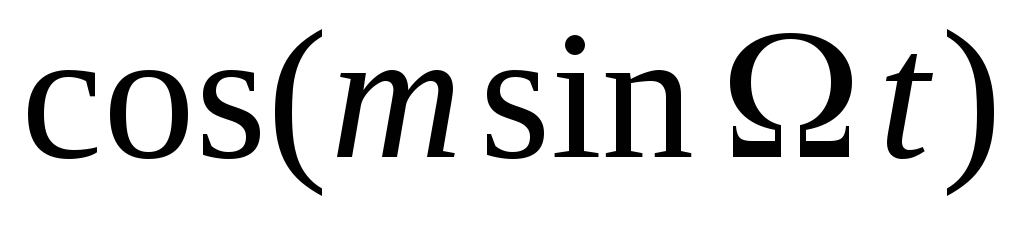
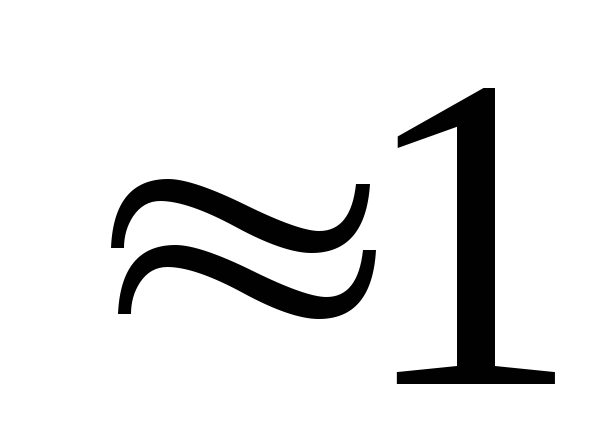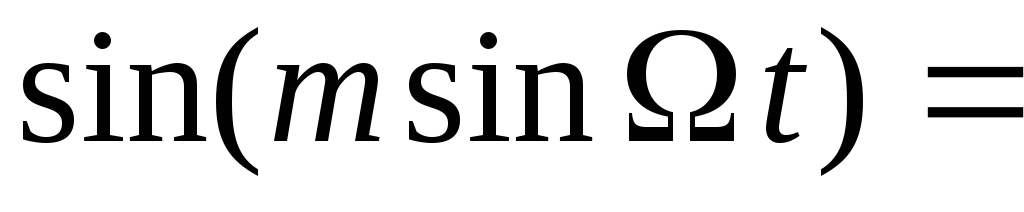
1. Для случая, когда ,,, 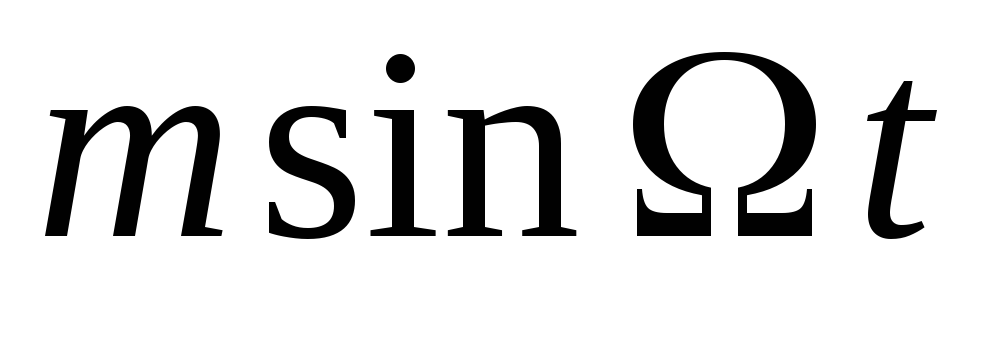следовательно, выражение (6) примет вид

. (7)

Используя выражение для косинуса суммы двух углов, получим

. (8)

Из (8) следует, что спектр ЧМ-сигнала аналогичен спектру АМ-сигнала (см. работу № 3). Он состоит из несущего колебания с частотой и амплитудой, нижнего и верхнего боковых колебаний с частотами соответственно,и амплитудами. Принципиальное отличие спектров состоит в том, что вектор нижнего бокового колебания повернут на 180 по отношению к вектору нижней боковой АМ-колебания (рис. 2а). На рис. 2б показан спектральный состав ЧМ-сигнала при .

у

u_ЧМ

х

u_в.б.

u_н.б.

u_m

t

t

t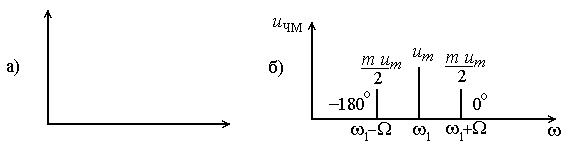

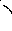
Рис. 2. Векторная диаграмма ЧМ колебания (а); спектр ЧМ-колебания (б).

2. Рассмотрим спектр ЧМ-колебания при условии, что 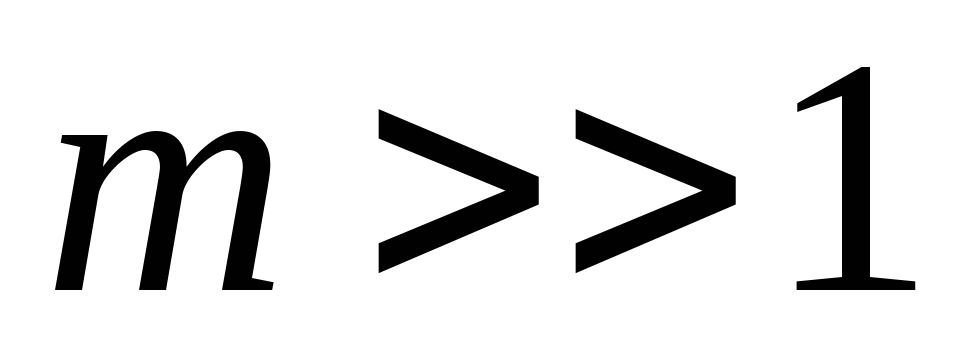. Для этого случая характерна высокая помехоустойчивость сигнала, поэтому большинство радиопередающих устройств работает именно при. Для получения выражения для ЧМ-сигнала необходим аппарат функций Бесселя. Известно, что

, (10)

, (11)

где – функции Бесселяn-го порядка. Соотношения (10) и (11) получены при разложении в ряд Фурье левых частей этих равенств. Подставляя выражения (10) и (11) в соотношение (5) с учетом, что при отрицательном порядке значение , получим

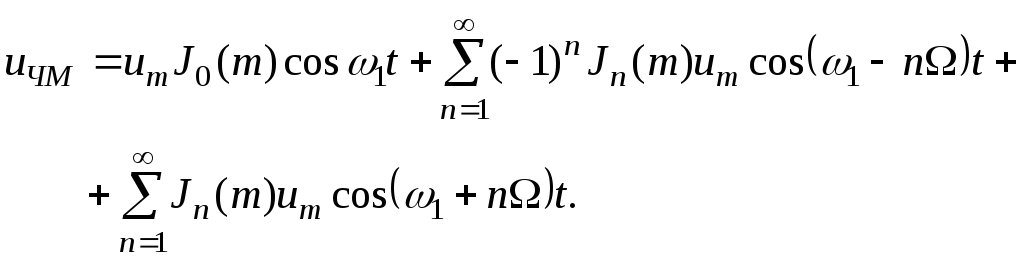(12)

Из выражения (11) видно, что спектр ЧМ-сигнала при однотональной модуляции при состоит из несущего колебания с частотойи амплитудойи бесконечного числа нижних и верхних боковых составляющих с частотами,и соответственно амплитудами,. Следует отметить, что нечетные нижние боковые повернуты относительно несущего колебания на 180. Теоретически спектр ЧМ-колебания является бесконечно широким. Для практической оценки ширины спектра учитывают ограниченное число гармоник, равных . Поэтому практическая ширина спектра равна:

. (13)

В случае произвольного сигнала (речь, музыка и др.) под  понимается наивысшая частота в спектре модулирующего сигнала (кГц). При радиовещании. Поэтому полоса занимаемых частот враз выше, чем при АМ-сигналах.