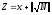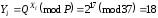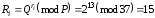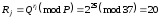1) Факторизуємо модуль n і визначаємо прості числа p та q;

2) знаходимо значення функції:

;

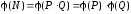3) розв’язуємо рівняння:

.

Факторизацію виконуємо, використовуючи метод двійкового решета.

Спочатку визначаємо базу розкладу – прості невеликі числа р1, р2 , ... рr , добуток яких Р_б є близьким до N=3599.

.

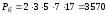Знаходимо .

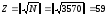Будуємо таблицю аналогічно як у задачі 1, пп. 1.14.

Таблиця 2.25 – Розрахунки

x		Z2mod3599	2	3	5	7	17	залишок
1	60	1	─	─	─	─	─	1
2	61	122	1	─	─	─	─	61
3	62	245	─	─	1	2	─	─
4	63	370	1	─	1	─	─	37
14	73	1730	1	─	1	─	─	173
23	82	3125	─	─	5	─	─	─
26	85	27	─	3	─	─	─	─
49	108	867	─	1	─	─	2	─
61	120	4	2	─	─	─	─	─
62	121	245	─	─	1	2	─	─

Беремо рядки зі значеннями x=3 та x=62, в результаі маємо:

;

.

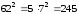Перемноживши рядки, маємо:

або

.

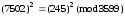Знайшовши залишок від значення 7502, маємо

.

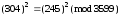Отже x=304 , y=245.

Далі

НОД (│304-245│,3599)=59=Р,

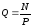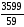==61.

Отже Р=59, Q=61.

Далі знаходимо

.

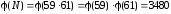Тепер ключовий розв’язок має вигляд

.

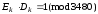Після переходу до рівняння

,

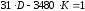подамо його у вигляді

.

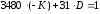Розв’язуємо це діафантове рівняння , використовуючи ланцюгові дроби

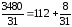; r0=112;

; r1=3;

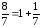; r2=1;

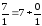; r3=7; μ=3;

;

;

;

;

.

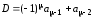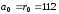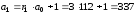Перевіримо правильність розв’язку

.

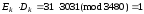Таким чином E_k=31; D_k=3031.

2.15 Криптографічні протоколи виробки та установки ключів. Приклади розв’язку задач та задачі для самостійного розв’язання

2.15.1 Приклади розв’язку задач

Задача 1.

Синтезуйте повний протокол узгодження та установки ключів, використовуючи криптографічні перетворення в групі точок ЕК. Обґрунтуйте та виберіть розміри загальносистемних параметрів та ключів.

Розв’язок задачі.

Згідно з вимогами міжнародного стандарту ISO-15946-3 та стандарту США X9.63 повний протокол-примітив базується на використанні довгострокових та сеансових ключів. Нехай криптографічні перетворення здійснюються над простим полем Галуа GF(P). Тоді довгостроковими загальносистемними параметрами є:

• A та B – параметри кривої y² = x² + Аx + В (mod P);

• порядок кривої u та порядок поля P;

• коефіцієнт ковариації h (u = 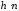, деn порядок базової точки G).

Як загальносистемні параметри, що використовуються при формуванні сеансових ключів, можуть бути як загальносистемні параметри виробки довгострокових ключів так і інші загальносистемні параметри. Ми вибираємо різні криві і відповідно різні базові точки та ключі.

Загальносистемними параметрами сеансових ключів є:

a_l, b_e, u_e, h_e, P_e, d_e,a, Q_e,a, d_e,b, Q_e,b .

Для довгострокових ключів загальносистемними параметрами є:

a_s, b_s, u_s, h_s, P_s, d_s,a, Q_s,a, d_s,b, Q_s,b.

В подальшому розглянемо випадок, коли загальносистемні параметри та базова точка при криптографічних перетвореннях будуть однакові для формування як довгострокових ключів так і сеансових.

Далі довгострокові відкриті ключі сертифікуються та висилаються кореспондентам A та B згідно з рис. 2.30.

Q_s,a

A B

d_s,a Q_s,b d_s,b

Рисунок 2.30 – Висилання сертифікованих ключів

Виробляємо загальні довгострокові секрети

;

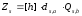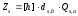
Сеансові ключі виробляються згідно з рис. 2.31

Q_e,a

A B

d_e,a Q_e,b d_e,b

Рисунок 2.31 – Виробка сеансових ключів

Короткострокові загальні секрети є

; .

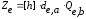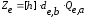Загальний секрет на сеанс виробляємо як 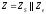. Сеансів ключ обчислюємо, як:,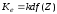

де kdf – є геш або друга функція.

Тепер обґрунтуємо порядок базової точки n з кута зору стійкості, вважаючи, що секретним є тільки сеансовий ключ d_s. Найбільш простим (швидким) на сьогодні методом роз’язку дискретного логарифмічного рівняння в групі точок ЕК є метод 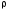–Полларда. Його складність визначається як

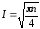. (2.143)

Якщо потужність криптоаналітичної системи є 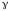, тоді безпечний час є

.

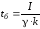Нехай років, а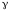=10¹⁰ операцій складання на ЕК/с, тоді

,

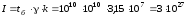де k = с/рік.

Знаходимо із рівняння n

.

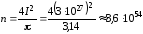В двійковому поданні довжина e в бітах

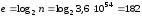бітів.

Якщо секретними є як довгостроковий так і короткостроковий ключі, тоді складність роз’язку двох рівнянь

.

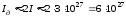Якщо I_д обмежений I, тобто

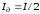
і

.

Тому

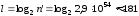біт.

Таким чином, вибираючи модулі з довжиною більше 182 бітів, можна забезпечити заданий рівень стійкості.

Задача 2.

Розробіть однопрохідний протокол з використанням довгострокових (головних) ключів на основі криптоперетворень в групі точок ЕК. Визначте необхідну величину порядку базової точки, якщо необхідно забезпечити захист від криптоаналітика з потужністю 10¹⁴ операцій складання на ЕК/с. з t_б = 10¹⁰ років (при імовірності успішного криптоаналізу P_k 10^-2).

Розв’язок задачі.

Виробку ключів зображено на рис. 2.32

Q_s,b

A B

d_s,a Q_s,a d_s,b

Q_e,a

d_e,a

Рисунок 2.32 – Виробка ключів

;

;

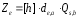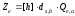
Загальний секрет Z виробляємо

Z = Z_s || Z_e

і далі аналогічно як і в задачі 1.

Вважаючи, що для розв’язку дискретних логарифмічних рівнянь в групі точок ЕК застосовується метод 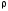–Полларда для розв’язку рівнянь

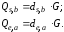
Необхідно застосувати криптоаналітичну систему з потужністю 2I, де I – потужність, необхідна для розв’язку одного рівняння.

Оскільки 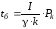, то

.

Далі із рівняння (2.143)

.

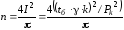Порядок базової точки в бітах визначаємо як

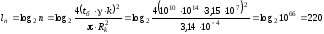бітів.

Задача 3.

Нехай виробка загального секрету здійснюється за схемою Діфі-Хеллмана в полі GF(97) причому твірний елемент 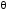=5 для користувачівA та B. Необхідно виробити загальний секрет.

Розв’язок задачі.

Кореспондент A генерує особистий ключ X_a, скажімо X_a = 36.

Кореспондент B генерує особистий ключ X_b, скажімо X_b = 58.

Далі кореспонденти A та B обчислюють свої відкриті ключі

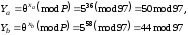
та обмінюються ними між собою.

Загальні секрети виробляються як

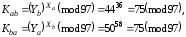
оскільки

,

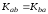то ключ вироблено правильно.

Задача 4.

Ключі криптографічного перетворення виробляються відповідно до протоколу з використанням схем Діфі-Хеллмана. Розробіть протоколи виробки ключів, якщо перетворення здійснюється в полі GF(P), P=37.

Розв’язок задачі.

Загальносистемними параметрами в схемах Діфі-Хеллмана є просте число Р=37 та твірний елемент Q. Оскільки Q не відомо, то виберемо його, перевіривши виконання умов:

де 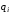– співмножники канонічного розкладуР-1.

Розкладаємо Р-1: 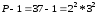. ОтжеQ буде твірним, якщо

Вибираємо випадкове значення Q=2. Обчислюємо

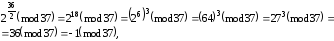
таким чином і умова про твірний елемент виконується.

Обчислюємо

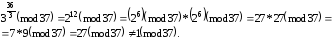
Таким чином, Q=2 – твірний елемент. Зазначимо, що всього для простого Р існує 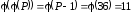твірних елементів.

Генеруємо довгострокові ключі для А_і та А_j користувачів:

Ai	Aj
Xi=17	Xj=11

Сертифікуємо Y_i та Y_j і розсилаємо сертифікати Y_i та Y_j . В результаті у А_i є Х_і , Y_j та Y_i ; у А_j є Х_j , Y_j та Y_i . На кожному сеансі зв’язку формуються сеансові ключі:

Ai	Aj
rri=17	rj=11

Загальний секрет формується таким чином:

Користувач А_і розраховує загальний секрет, як

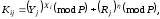
а користувач A_j як

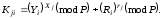
Підставивши значення, маємо

,

.

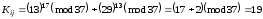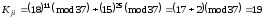Таким чином 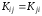і кореспондентиA_i та A_j виробили однаковий загальний секрет. Цей загальний секрет може бути використаний як у явному вигляді, так і за рахунок відповідного перетворення.