5.8 Частотная модуляция с минимальным сдвигом.

Чатотная модуляция с минимальным сдвигом (MSK- minimum shift keying) это метод модуляции у которого сглаживание фронтов импульсов

осуществляется по закону гармонической фуекции. Вобщем случае модулированное колебание может быть записано в виде:

где ,.

Функции I_i(t) и Q_i(f) определяется моделирующим колебанием и могут быть записаны в виде

I_i(t) = a_ip(t); Q_i (t)= b_iq(t),

где p(t) и q(t)моделирующие колебания, обеспечивающие

скругление фронтов передаваемых посылок; a_i и b_i - символы нечетных и

четных посылок, равные 1.

При передаче прямоугольных импульсов

В результате можно записать следующее равенство.

Символы а_i и b_i в квадратурных каналах могут быть смещены

относительно друг друга на Т_c.

Одна из широко применяемых форм скругления фронтов соответствует

следующему виду функций p(t) и q(t)

В этом случае будет справедливо выражение

Текущая фаза такого сигнала в произвольный момент времени равна

,

а мгновенная частота

.

Моделирующие символы в квадратурных каналах a_i и b_i имеют длительность Т_c . Основная моделирующая частота , девиация частоты, индекс частотной модуляции. Посколькуa_i и b_i равны , возможны четыре варианта модулированного сигнала:

Из этих выражений видно, что фаза выходного напряжения за изменяется на .

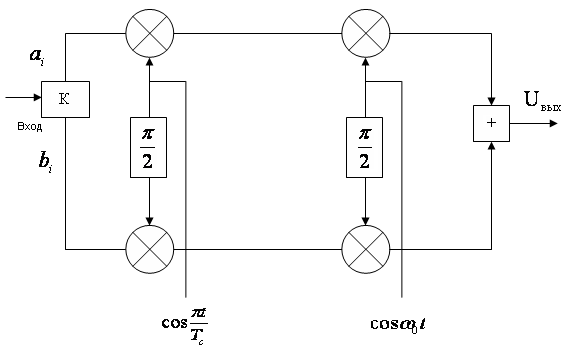
Рис.5.24 Стуктурная схема модулятора

На этом рисунке обозначены:

K – коммутатор, распределяющий нечетные и четные посылки по каналам;

- фазовращатель на ;

- перемножитель;

+ - сумматор.

Прием сигналов осуществляется с помощью фазового детектора, который обеспечивает умножение принимаемого колебания на опорное и интегрирование. Опорное напряжение равно .

В результате приема четырех моделированных колебаний на выходе получим четыре сигнала:

1)

2)

3)

4)

Здесь чертой обозначено интегрирование.

Таким образом, в течение интервала напряжение на выходе демодулятора принимает одно из двух возможных значений:.

Изменение вида напряжения показано на рисунке 5.25

Рис. 5.25 Эпюры напряжения.

Учитывая ранее приведенные выражения, можно утверждать, что при напряжении на выходе модулятора, равным , передавались 11 или 10, а при напряжении- передавались 01 или 00 (рис. 5.25). Следовательно при выходном напряжениипервый символ 1, а при- первый символ 0. Значение второго символа определяется по виду выходного напряжения на следующем временном интервале длительностью.

Так как в пределах длительности посылки фаза изменяется непрерывно и линейно, ширина спектра. сигнала снижается. Спектр частот достаточно компактен. При этом главный лепесток огибающей спектра сигнала включает 99,5% мощности сигнала.

Частотная модуляция с минимальным сдвигом находит широкое применение в стандарте сотовой связи GSM. С целью уменьшения ширины спектра частот последовательность информационных бит до модулятора проходит через фильтр с характеристикой вида гауссовой кривой и поэтому модуляция называется гауссовской. Применение такого фильтра позволяет при дискретном изменении частоты получить «гладкие переходы». В результате удается получить произведение равным 0,3.