5.3. Помехоустойчивость при приеме сигналов с различными видами модуляции.

Рассмотренные в предыдущем разделе методы оптимального приема, которые обеспечивают потенциальную помехоустойчивость, предполагают идеальное согласование сигналов с характеристиками каналов связи и являются предельно достижимыми. Поэтому важно уметь оценивать помехоустойчивость при применении разнообразных видов модуляции для реального приема сигналов. Наибольшие трудности в технической реализации возникают при когерентном приеме сигналов. Поэтому при применении АМ и ЧМ наиболее распространен некогерентный способ приема этих сигналов.

Широкое применение нашли средства относительной и двукратной относительной фазовой модуляции. В них удалось преодолеть принципиальные трудности, которые продолжительное время препятствовали практическому использованию ФМ. В данном разделе излагается методика оценки помехоустойчивости при использовании различных видов модуляции.

5.3.1. Помехоустойчивость при приеме амплитудно-моделированных сигналов.

При использовании АМ справедливы выражения . Напряжение канального сигнала записывается в виде

, где

- порядковый номер символа;

- номер позиции кода с основанием ;

- функция, описывающая форму импульсного сигнала;

- коэффициент амплитудной модуляции.

Структурная схема демодулятора АМ сигналов приведена на рис. 5.8.

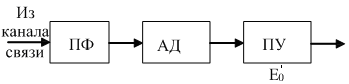
Рис. 5.8. Структурная схема демодулятора АМ сигнала.

Единственным критерием, который позволяет различать элементы, соответствующие 1 и 0, есть величина амплитуды колебаний. Если напряжение на выходе детектора приемника превышает некоторое пороговое значение, то фиксируется сигнал 1, если это напряжение ниже, то фиксируется сигнал 0. В соответствии с этим демодулятор двоичных АМ сигналов, структурная схема которого приведена на рис.5.8, состоит из полосового фильтра ПФ, который обеспечивает защиту от сосредоточенных помех и снижение уровня флуктуационных помех, амплитудного детектора (АД), выделяющего огибающую принимаемого сигнала, и порогового устройство (ПУ) с порогом .

Ошибки при приеме возникают, если при передаче 1 суммарное напряжение сигнала и помехи на выходе приемника будет ниже порога, т.е., и если при передаче0 напряжение помех окажется больше , т.е..

Поскольку при передаче данных вероятности передачи 1 и 0 обычно равны, т.е. Р(1) = Р(0) = 0,5, то справедливо выражение

. (5.7)

Плотность вероятности огибающей суммы синусоидального сигнала и помехи на выходе детектора подчиняется обобщенному закону Релея

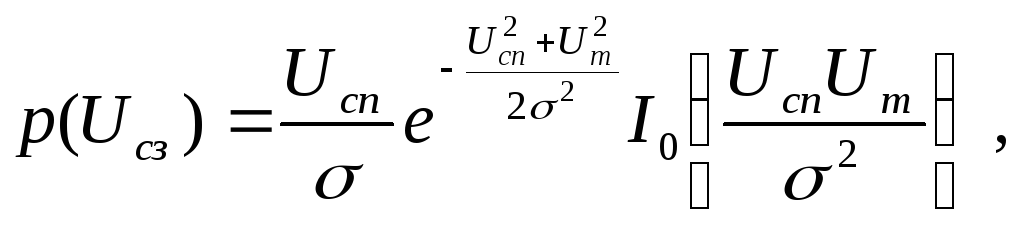
где значение огибающей суммы сигнала и помехи;

- модифицированная функция Бесселя нулевого порядка.

Считая , получим распределение вероятности для огибающей помехи(простой законРелея)

.

В соответствии с приведенными на рис.5.9 зависимостями распределения для иможно определить вероятности ошибок Р(0/1) и Р(1/0):

;

.

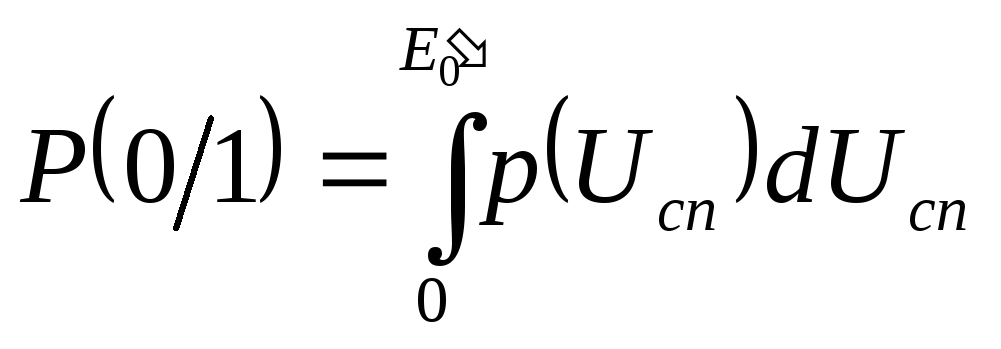Рис. 5.9 К выводу вероятности ошибки

В общем случае Р(0/1)Р(1/0), т.е. при некогерентном приеме АМ сигналов канал несимметричный.

Подставив значение ив (5.7), получим:

(5.8)

где: ;;,

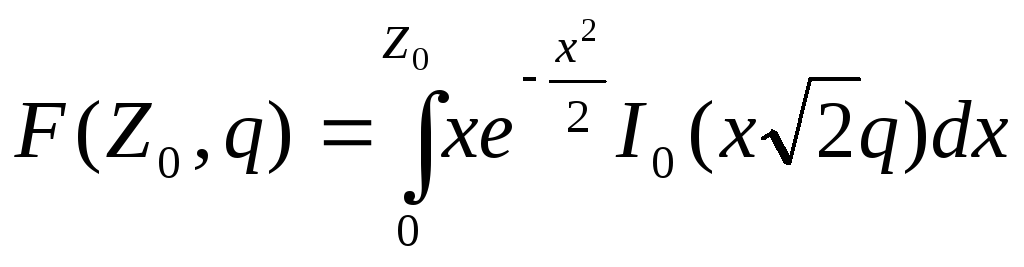где: _ эффективное напряжение сигнала.

Как видно из выражения (5.8), величина зависит от отношения сигнал / помеха и от величины порога .

Существует оптимальное значение порога, который зависит от величины q. На рис.5.10 показана зависимость относительного значения порога от отношения сигнал / помеха по напряжениюq. Из этого рисунка видно, что при большом значении q величина стремится к 0,5.

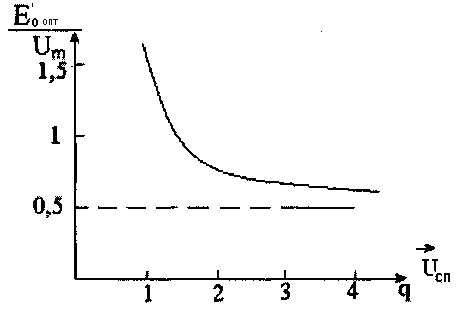
Рис.5.10 зависимость

Для ориентировочных расчетов вероятности ошибки при воздействии флуктуационных помех при q>3 и можно использовать формулу:

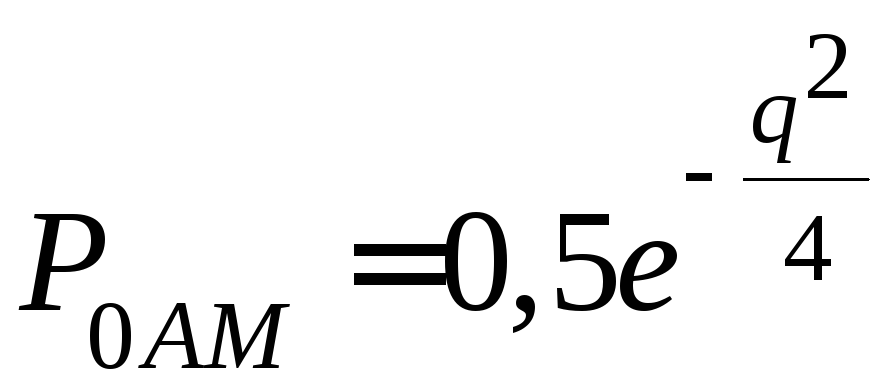(5.9)

при этом основная часть ошибок обусловлена вероятностью «ложных тревог». График зависимости вероятности ошибки от отношения сигнала к шуму по мощности приведен на рис.5.11:

Рис.5.11 Зависимость