Определение. Точка области определения функции называется стационарной, если в этой точке существуют частные производные первого порядка, и выполняется необходимое условие экстремума:

.

Достаточное условие экстремума

Теорема. Пусть в окрестности стационарной точки функцияимеет частные производные до третьего порядка включительно. Обозначим:

; ;;.

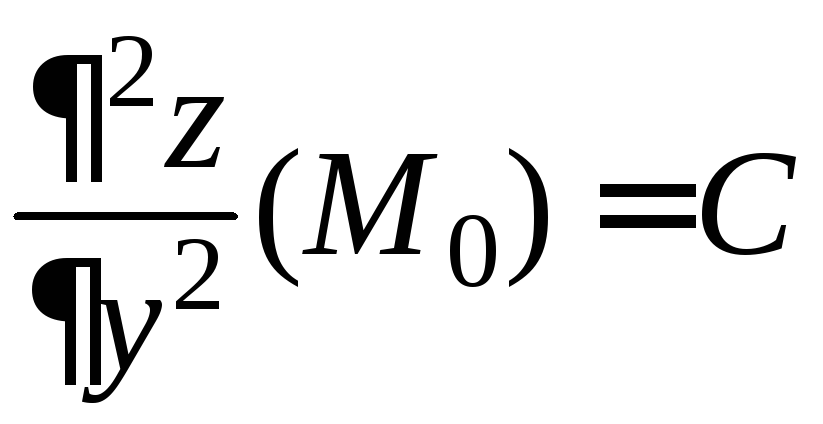Тогда:

1. Если , то в точкеэкстремума нет.

2. , то в точке имеется экстремум; при этом:

если , то— точка максимума;

если , то— точка минимума.

(без доказательства).

Замечание. Если , то для решения вопроса о наличии экстремума требуется привлечение производных более высоких порядков.

Пример. Рассмотрим функцию

.

Здесь

; .

Решая систему уравнений, находим стационарные точки путем решения системы уравнений:

.

Функция имеет единственную стационарную точку . Находим частные производные второго порядка:

; ;.

Далее, , и. Значит,— точка минимума.

14. Производная по направлению и градиент

I. Направляющие косинусы вектора

Н

апомним, что для ненулевого вектораплоскости или пространства его направляющими косинусами называются косинусы углов, которые этот вектор образует с осями декартовой системы координат (рис. 19).

Если ненулевой вектор плоскости имеет в ортонормированном базисе, связанном с этой системой, координаты, то есть, то

; .

Аналогично в случае ненулевого вектора пространства формулы для направляющих косинусов имеют вид:

; ;

.

Направляющие косинусы вектора задают его направление в пространстве. Вектор , координатами которого являются направляющие косинусы вектора, сонаправлен с вектороми имеет модуль, равный единице (рис. 20).

II. Понятие производной по направлению

Пусть в области плоскостизаданы функция двух переменных, точка, и ненулевой вектор . Будем выбирать переменную точкутаким образом, чтобы векторбыл сонаправлен с вектором(рис. 21).

Обозначим приращения независимых переменных при переходе от точки к точкечерез,; соответств

ующее приращение функции через. Тогда

.

Определение. Пусть стремится к точкетаким образом, что векторостается направленным одинаково с вектором. Если существует конечный предел отношенияпри, то этот предел называетсяпроизводной функции по направлению вектора в точке  .

Обозначение производной по направлению: . Итак, согласно определению:

.

Замечание. Производная по направлению показывает скорость изменения функции в точке в направлении вектора. В частности производные по направлению базисных ортов равны соответствующим частным производным:

.

Пусть вектор имеет направляющие косинусы,.

Теорема. Пусть функция удовлетворяет двум условиям:

1. В окрестности точки она имеет частные производные .

2. В самой точке частные производные непрерывны.

Тогда для производной по направлению справедлива формула:

. (24)

Доказательство. Пусть ,— приращения независимых переменных, соответствующие переходу от точкик точке. Ввиду непрерывности частных производных для соответствующего приращения функциисправедлива формула:

, (25)

где функции и― бесконечные малые величины прии(п. 6). Деля обе части (25) на, получаем:

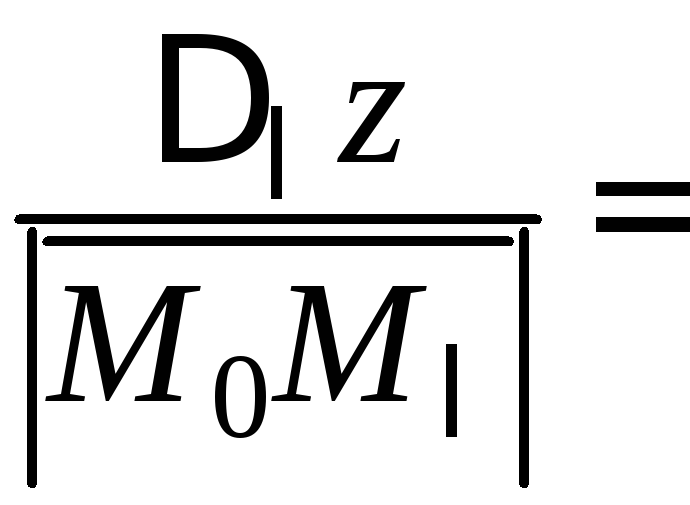
. (26)

Поскольку вектор сонаправлен с вектором, то величина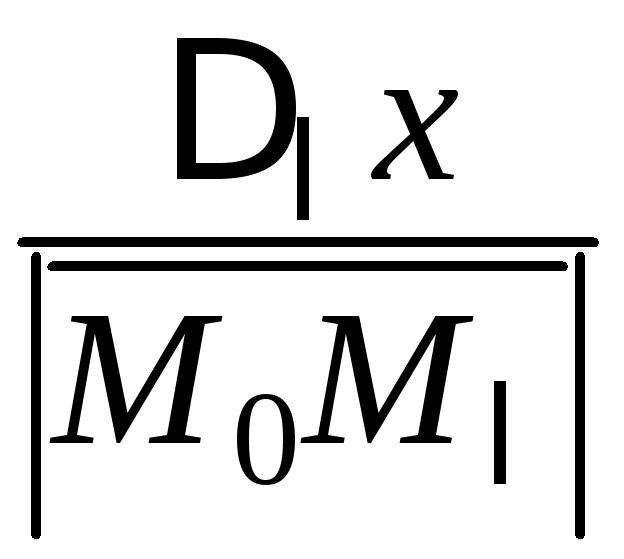, будучи направляющим косинусом вектора, совпадает с направляющим косинусом вектора:. Аналогично.

Равенство (26) теперь принимает вид:

. (27)

Поскольку ,, когда, то переходя в (27) к пределу при, получаем на основании свойств предела:

. ▄

Пример. Пусть ,,. Вычислим производную по направлению. Находим частные производные:

; ;

; .

Находим направляющие косинусы вектора :

; .

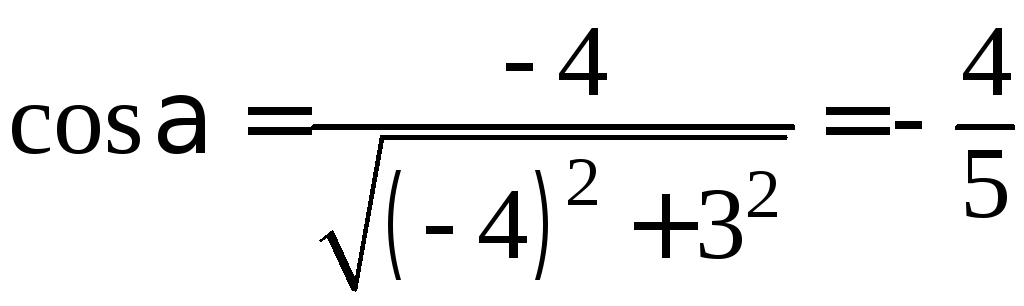Подставляем найденные значения в формулу (24):

.

Аналогичным образом определяется производная по направлению в случае функции трех или более переменных. Для функции трех переменных формула (24) (в случае непрерывности частных производных) принимает вид:

.