6. Дифференцируемость функции нескольких переменных

I. Понятие дифференцируемости

Напомним, что для функции одной переменной дифференцируемость в точкепо определению означает существование конечного предела

.

Необходимым и достаточным условием для этого является возможность представления приращенияв точкев виде:

, (1)

где является бесконечно-малой величиной; при этомявляется, как функция переменной, бесконечно малой величиной более высокого порядка, чем [4].

В случае функции нескольких переменных в основу понятия дифференцируемости кладется условие, аналогичное (1).

Итак, пусть функция определена в окрестности точки.

Определение. Функция называетсядифференцируемой в точке , если ее полное приращение в этой точке, как функция аргументови, представимо в виде:

, (2)

где функция является прибесконечно малой величиной более высокого порядка, чем(рис. 9).

В этом случае выражение , являющееся линейной функцией аргументови, называетсяполным дифференциалом функции в точке.

З

амечание. Из дифференцируемости функции в точкеследует ее непрерывность в этой точке, поскольку из (2) следует: .

Теорема. Если функция дифференцируема в точке, то в этой точке существуют частные производные, и коэффициентыив формуле(2) равны их значениям:

.

Доказательство. Положим в формуле (2) и устремимк нулю. При этомстановится частным приращением, и (2) принимает вид:

,

откуда

, (3)

причем

,

так что в соответствии с условием на и ввиду ограниченности величины: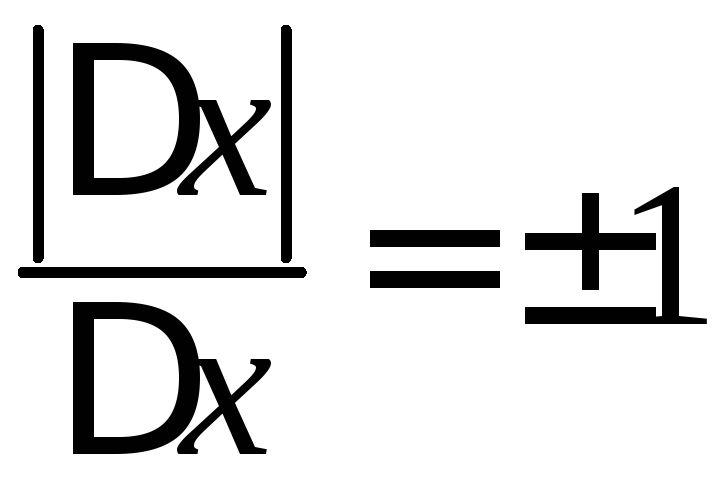

Переходя в равенстве к пределу при , получаем:.

Аналогично устанавливается равенство .▄

Таким образом, полный дифференциал имеет вид:

.

Из формулы (2) следует, что при малых по модулю иимеет место приближенное равенство полного приращения и полного дифференциала, которые отличаются на бесконечно малую величину более высокого порядка, чеми.

II. Формула для полного приращения

Теорема. Пусть функция удовлетворяет двум условиям:

1. В окрестности точки она имеет частные производные .

2. В самой точке частные производные непрерывны.

Тогда для полного приращения в точкесправедлива формула :

, (4)

где частные производные вычислены в точке , а функции являются приибесконечно малыми величинами.

Доказательство.

(см. рис. 7).

Разность

можно рассматривать как разность двух значений функции

,

зависящей от одной переменной , причем ее производная является частной производной поисходной функции:. По теореме Лагранжа [4]:

,

где промежуточная точка , и потому.

Аналогично разность

можно рассматривать как разность двух значений функции , зависящей от одной переменной, причем ее производная является частной производной по исходной функции :. По теореме Лагранжа:

,

где промежуточная точка , и потому.

Итак,

. (5)

Воспользуемся теперь непрерывностью частных производных в точке :

.

Отсюда по теореме о структуре сходящейся переменной [4]):

;

,

где функции являются бесконечно малыми величинами при и . Подставляя эти выражения в (5), получаем (4). ▄