Р ис. 6

2. Предел функции нескольких переменных

Пусть точка является для области определенияфункциивнутренней или граничной, так что в любой ееокрестности (то есть сколь угодно близко от нее) содержатся точки области.

Определение. Число называетсяпределом функции вточке (говорят также:при или при ), если для любого(сколь угодно малого) существует, такое что при выполнении условийсправедливо неравенство.

Обозначения:

; ;;

.

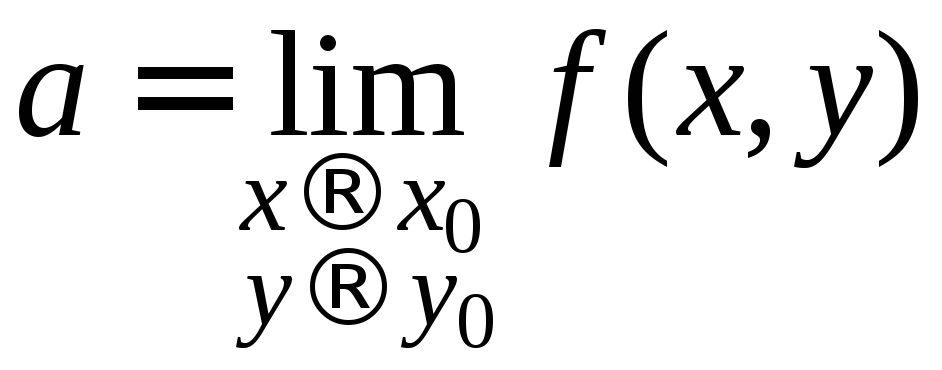Аналогично определяется предел функции трех или более переменных.

Замечания. 1. Геометрически утверждение о том, что , означает, что значения функциисколь угодно близко приближаются к числу, если точка, оставаясь в области определения, достаточно близко подходит к точке.

2. Предел функции нескольких переменных обладает cвойствами, аналогичными свойствам предела функции одной переменной [1]. Мы будем использовать их по мере необходимости.

3. Приращения функции нескольких переменных

Пусть ―фиксированная точка области определения функции, а приращениянезависимых переменныхине выводят переменные точки

,

за пределы (рис. 7).

О

пределение. 1. Полным приращением функции в точке называется разность

.

Для фиксированной точки полное приращениеявляется функцией переменных, которая определена при всех достаточно малых по модулю.

2. Частным приращением функции в точке по переменной называется разность

.

Для фиксированной точки частное приращениеявляется функцией переменной, которая определена при всех достаточно малых по модулю.

Аналогично частным приращением функции в точке по переменной называется разность

.

Для фиксированной точки частное приращениеявляется функцией переменной, которая определена при всех достаточно малых по модулю.

Пример. Рассмотрим функцию . Ее полное приращение

Частные приращения:

Если , то в точке:

; ;.

Аналогично определяются полное и частные приращения функции большего числа переменных. Например, для функции :

;

;

;

.

4. Непрерывность функции нескольких переменных

Пусть функция нескольких переменных задана в области, точкапринадлежит.

Определение. Функция непрерывна в точке , если ее предел в этой точке равен значению функции в самой точке:

.

Это означает, что близким к точкамсоответствуют близкие кзначения функции.

Определение. Функция непрерывна в области , если она непрерывна в каждой точке этой области.

Для функции двух переменных это геометрически означает, что поверхность графика функциине имеет скачков, разрывов, является непрерывной в интуитивном смысле.

Аналогично определяется непрерывность в точке и области для функции большего числа переменных.

Теорема (критерий непрерывности в терминах приращений). Для того, чтобы функция была непрерывна в точке, необходимо и достаточно, чтобы бесконечно малым (стремящимся к нулю) приращениям независимых переменныхисоответствовало бесконечно малое приращение функции:.

Доказательство. По свойствам предела:

. ▄

5. Частные производные

Пусть функция определена в окрестности точки.

Определение. Частной производной функции в точкепо переменной называется предел отношения частного приращения в этой точке к вызвавшему его приращениюпеременнойпри.

Обозначения частной производной:

Итак, согласно определению,

.

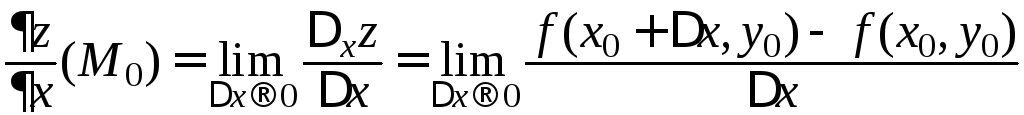Аналогично

.

Таким же образом определяются частные производные для функции большего числа переменных. Например, для функции :

.

При вычислении частной производной по переменной все остальные независимые переменные считают постоянными величинами (равными соответствующим координатам точки ), и применяют правила дифференцирования функции одной переменной [4].

Примеры. 1. .

(производная второго слагаемого равна нулю как производная константы);

.

2. .

.

3. . Частная производная по переменнойявляется производной степенной функции с фиксированным показателем; поэтому. Частная производная по переменнойявляется производной показательной функции с фиксированным основанием; поэтому.

4. . По правилу дифференцирования сложной функции:

;

.

5. .

.

6. .

.

Геометрический смысл частных производных

Частная производная функции по переменной

в точке является обычной производной функциив точке.

График функции , сдвинутый из координатной плоскости вдоль оси, является линией пересечения поверхностис плоскостью, параллельной координатной плоскости(рис. 8). Поэтому частная производнаяравна тангенсу угланаклона касательнойк оси; при этом точкаявляется проекцией точкина плоскость.