
- •Федеральное агентство морского и речного
- •II. Понятие области
- •III. Определение функции
- •Р ис. 6
- •3. Приращения функции нескольких переменных
- •5. Частные производные
- •6. Дифференцируемость функции нескольких переменных
- •I. Понятие дифференцируемости
- •II. Формула для полного приращения
- •III. Достаточное условие дифференцируемости
- •IV. Соотношение понятий непрерывности, дифференцируемости и частных производных
- •7. Частные производные сложной функции
- •8. Полная производная сложной функции
- •9. Дифференцирование неявной функции
- •10. Уравнения касательной к пространственной линии
- •Как и в случае плоской кривой, имеет место следующее Определение. Касательной к линии в точке называется предельное положение секущей при .
- •11. Уравнение касательной плоскости и уравнения нормали к поверхности
- •Уравнения нормали к поверхности
- •(Без доказательства).
- •13. Экстремумы
- •Необходимое условие экстремума
- •Определение. Точка области определения функции называется стационарной, если в этой точке существуют частные производные первого порядка, и выполняется необходимое условие экстремума:
- •II. Понятие производной по направлению
- •III. Понятие градиента
- •IV. Связь производной по направлению с градиентом
- •Литература
- •Ястребов Михаил Юрьевич математика
- •Учебное пособие
Уравнения нормали к поверхности
О пределение.Прямая
пределение.Прямая
![]() ,
проходящая через точку
,
проходящая через точку![]() поверхности
поверхности![]() перпендикулярно касательной плоскости
перпендикулярно касательной плоскости![]() ,
называетсянормалью
к поверхности
в точке
,
называетсянормалью
к поверхности
в точке
![]() (рис. 17).
(рис. 17).
Направляющий
вектор нормали
![]() совпадает с нормальным вектором
касательной плоскости:
совпадает с нормальным вектором
касательной плоскости:
 .
.
Поэтому канонические уравнения нормали к поверхности имеют вид:

В последнем примере канонические уравнения нормали имеют вид:
 .
.
12. Частные производные высших порядков
Пусть
функция
![]() имеет в области
имеет в области![]() частные производные
частные производные .
Функции
.
Функции в свою очередь могут иметь частные
производные в области
в свою очередь могут иметь частные
производные в области![]() или более узкой области. Эти частные
производные называютсячастными
производными второго порядка
исходной функции
или более узкой области. Эти частные
производные называютсячастными
производными второго порядка
исходной функции ![]() .
.
У функции двух переменных могут быть четыре разных частных производных второго порядка:
1)
 ,
или в других обозначениях
,
или в других обозначениях![]() ;
;
2)
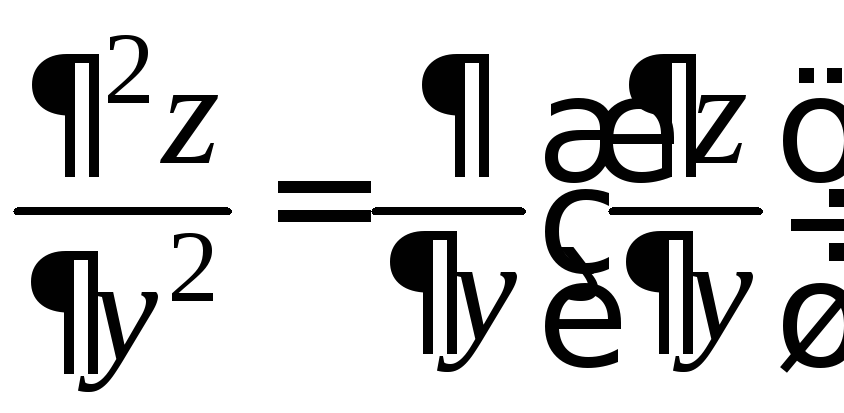 ,
или в других обозначениях
,
или в других обозначениях![]() ;
;
3)
 ,
или в других обозначениях
,
или в других обозначениях![]() ;
;
4)
 ,
или в других обозначениях
,
или в других обозначениях![]() .
.
Исходные
частные производные
 называются при этом частными
производными первого порядка.
называются при этом частными
производными первого порядка.
Аналогично определяются и частные производные более высоких порядков от функций двух и более переменных.
Пример.
У функции
![]() среди частных производных третьего
порядка имеются в том числе следующие:
среди частных производных третьего
порядка имеются в том числе следующие:
 ;
;
 ;
; .
.
и т. д.
Те из частных производных второго и более высоких порядков, у которых дифференцирование ведется по различным переменным, называются смешанными. Так, в последнем примере первые две из частных производных третьего порядка являются смешанными.
Пример.
Рассмотрим функцию
![]() .
Здесь
.
Здесь
 ;
;
 .
.
Далее,
 ;
;
 ;
; ;
;
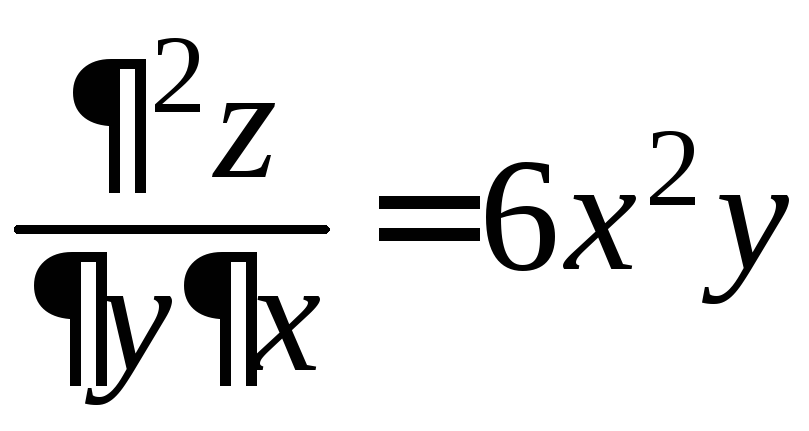 .
.
Совпадение
смешанных частных производных
 и
и в последнем примере является неслучайным;
именно справедлива следующая
в последнем примере является неслучайным;
именно справедлива следующая
Теорема. Пусть выполнены два условия:
1.
В окрестности точки
![]() существуют частные производные
существуют частные производные и
и .
.
2.
В самой точке
![]() смешанные частные производные
смешанные частные производные и
и непрерывны.
непрерывны.
Тогда имеет место равенство смешанных частных производных:
 .
.
(Без доказательства).
13. Экстремумы
Пусть
функция
![]() задана в области
задана в области![]() ,
содержащей точку
,
содержащей точку![]() .
.
Определение.
1. Точка
![]() называетсяточкой
максимума
функции
называетсяточкой
максимума
функции
![]() ,
если для всех точек
,
если для всех точек![]() из некоторой окрестности точки
из некоторой окрестности точки![]() выполняется неравенство
выполняется неравенство![]() (другими словами, точка
(другими словами, точка![]() являетсядля
этой окрестности
точкой наибольшего значения).
являетсядля
этой окрестности
точкой наибольшего значения).
2.
Аналогично точка
![]() называетсяточкой
минимума
функции
называетсяточкой
минимума
функции
![]() ,
если для всех точек
,
если для всех точек![]() из некоторой окрестности выполняется
неравенство
из некоторой окрестности выполняется
неравенство![]() .
.

Точки максимума и минимума называют точками экстремума.
Замечание.
Понятие точки экстремума является
локальной
характеристикой
функции, говорящей о ее поведении в
малой окрестности
точки
![]() .
В точках, далеких от
.
В точках, далеких от![]() ,
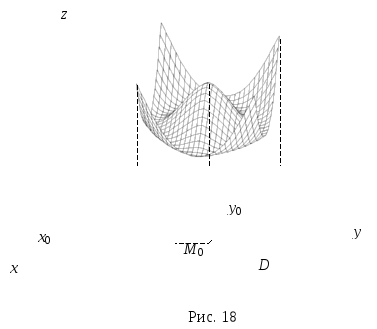
значения функции могут быть больше, чем
в точке максимума или меньше, чем в точке
минимума (рис. 18).
,
значения функции могут быть больше, чем
в точке максимума или меньше, чем в точке
минимума (рис. 18).
Необходимое условие экстремума
Теорема.
Если функция
![]() имеет в точке
имеет в точке![]() экстремум, то каждая из частных производных
экстремум, то каждая из частных производных ,
если она существует в этой точке, равна
нулю.
,
если она существует в этой точке, равна
нулю.
Таким
образом, необходимое условие экстремума
в точке
![]() в случае существования частных производных
имеет вид:
в случае существования частных производных
имеет вид:
 ;
;
 .
.
Доказательство.
Пусть например,
![]() — точка максимума, и в этой точке
существует частная производная
— точка максимума, и в этой точке
существует частная производная![]() .
Зафиксируем
.
Зафиксируем![]() и рассмотрим функцию одной переменной
и рассмотрим функцию одной переменной![]() .
Тогда
.
Тогда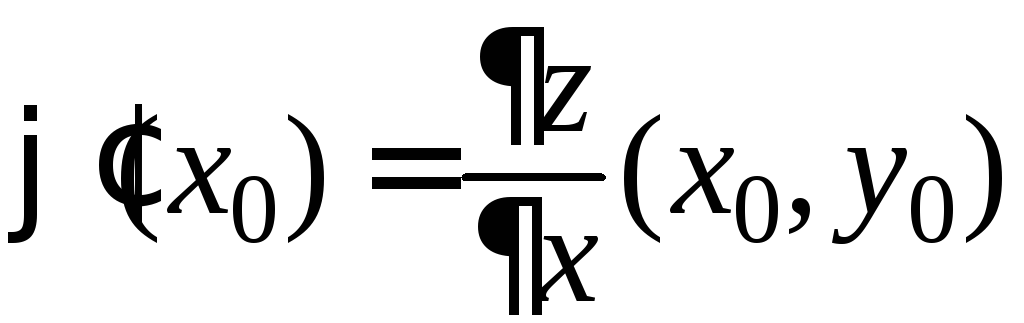 .
Из определения точки экстремума следует,
что
.
Из определения точки экстремума следует,
что![]() является для функции
является для функции![]() точкой максимума, и необходимое условие
экстремума для функции одной переменной
дает:
точкой максимума, и необходимое условие
экстремума для функции одной переменной
дает:![]() ,
то есть
,
то есть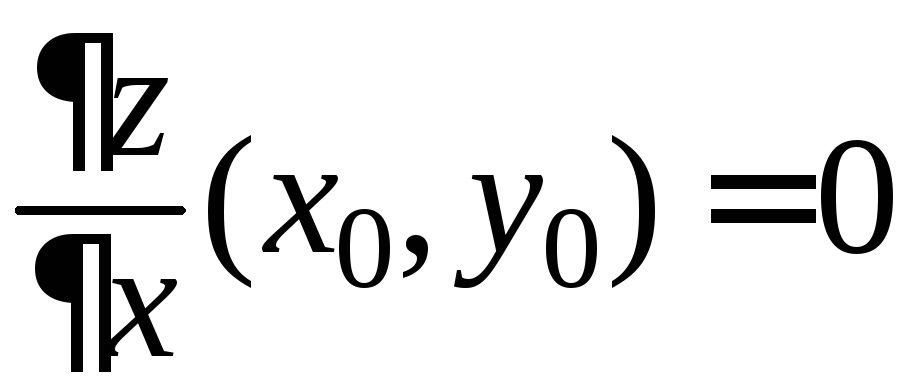 .
.
