20

Методические указания и контрольные задания для студентов заочного обучения в соответствии с рабочей программой учебной дисциплины МАТЕМАТИКА

Номер варианта контрольной работы по математике соответствует последней цифре учебного шифра студента:

Таблица вариантов:

№ варианта	Номера заданий
(последняя цифра шифра)
1	1	11	21	31	41	51	61	71	81	100
2	2	12	25	32	42	56	62	72	82	98
3	3	13	22	33	43	60	63	73	83	94
4	4	14	30	34	44	57	64	74	84	92
5	5	15	29	35	45	58	65	75	85	95
6	6	16	26	36	46	52	66	76	86	99
7	7	17	23	36	47	53	67	77	87	97
8	8	18	24	38	48	54	68	78	88	91
9	9	19	27	39	49	55	69	79	89	96
0, т.е. вариант 10	10	20	28	40	50	59	70	80	90	93

Перечень рекомендуемых учебных изданий, дополнительной литературы:

Основные источники:

1. Богомолов Н.В. Математика: учебник для ссузов./ Н.В. Богомолов, П.И. Самойленко – М.: Дрофа, 2006. – 395 с.

2. Богомолов Н.В. Сборник задач по математике: учебное пособие для ссузов / Н.В. Богомолов. – М.: Дрофа, 2006. - 204 с.

3. Омельченко В.П. Математика: учебное пособие / В.П. Омельченко. – М.: Феникс, 2007 – 380 с.

Дополнительные источники:

4. Валуцэ И.И. «Математика для техникумов», М., 1989.

5. Данко П.Е. Высшая математика в упражнениях и задачах (в двух частях)./ П.Е. Данко, А.Г. Попов, Г.Я. Кожевникова. - М.: 1996, 1997. – 304с.

6. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов./ Н.Ш. Кремер. – М.: ЮНИТИДАНА, 2006.-573 с.

7. Лунгу К.Н. Сборник задач по высшей математике/ К.Н. Лунгу.– М.: Айрис-прес, 2005.-576с.

8. Письменный Д.Т. Конспект лекций по высшей математике: полный курс/ Д.Т. Письменный. – М.: Айрис-прес, 2006.-608с.

9. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. / Д.Т. Письменный.– М.: Айрис-прес, 2006.-288с.

10. Яковлев Г.Н. Математика для техникумов: Алгебра и начала анализа. / Часть 1-2./ Г.Н. Яковлев. - М.: Наука, 1ч. 1987. – 464с., 2ч 1988. – 272с

ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ:

1. - 10. Вычислите пределы:

1. а) ; б) . 2. а) ; б) .

3. а) ; б) . 4. а) ; б) .

5. а) ; б) 6. а) ; б) .

7. а) ; б) . 8. а) ; б)

9. а) ; б) . 10. а) ; б) .

11. - 20. Найдите производную функции:

11. y = ln²cosx. 12. y = . 13. y = . 14. y=. 15. y=.

16. y = . 17. y = . 18. y =. 19. y = . 20. y = .

21. - 22. Найдите вторую производную функции:

21. y = x∙lnx – x. 22. y = 5∙lnx + x.

23.-28. Задачи на приложения производной:

23. Составьте уравнение касательной к графику в точке с абсциссой х = -2.

24. Составьте уравнение нормали к графику в точке с абсциссой х = -2.

25. Тело движется прямолинейно по закону s= 3 + 9t + 3t+ . Найдите ускорение движения тела в конце 3 секунды.

26. Тело движется прямолинейно по закону s= t³- 4t² + 5. Найдите ускорение движения тела в момент времени t=2 сек.

27. Найдите интервалы монотонности функции: у = .

28. Найдите интервалы выпуклости и вогнутости функции: у = .

29.-30. Найдите дифференциал функции:

29. y = - дифференциал первого порядка, 30. y = x∙lnx –7x - дифференциал второго порядка.

31.-40. Найдите интегралы:

31. а) ; б).32. а) ; б).

33. а) ; б).34. а) ; б).

35. а) ; б).36. а) ; б).

37. а) ; б).38. а) ; б).

39. а) ; б).40. а) ; б).

41.- 50. Вычислите интеграл:

41. 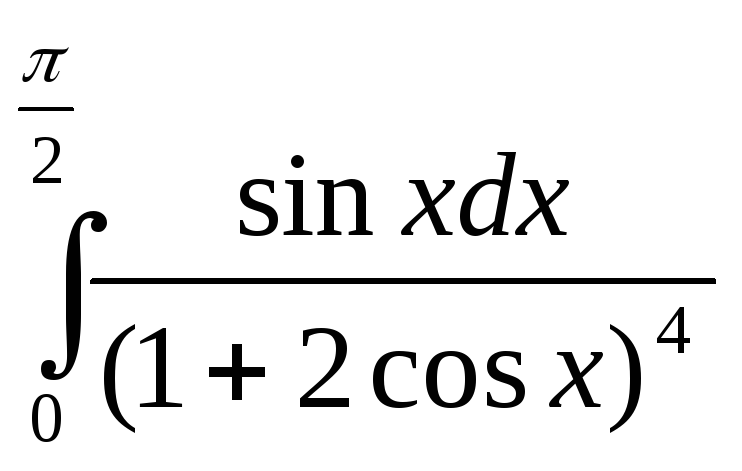. 42. . 43.. 44. . 45. .

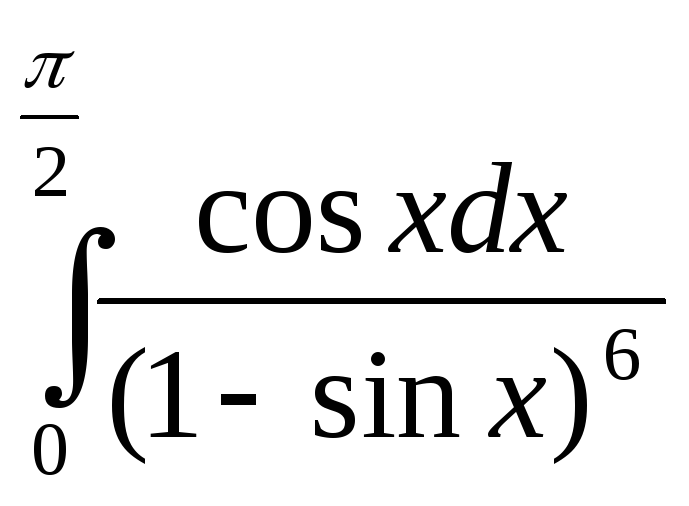46. . 47. . 48. . 49. . 50. .

50. Задачи на применение определенного интеграла:

51. Вычислите площадь фигуры, ограниченной линиями: .

52. Вычислите площадь фигуры, ограниченной линиями: .

53. Вычислите площадь фигуры, ограниченной линиями: .

54. Вычислите площадь фигуры, ограниченной линиями: и осью Ох.

55. Вычислите площадь фигуры, ограниченной осью Ох и линией.

56. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:

.

57.Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:

.

58.Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:.

59. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: .

60. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями:

.

61. – 70. Решите дифференциальное уравнение и найдите частное решение:

61. , при x=-4 y=1. 62. , y =4 при x= 0.

63. , y=3 при х=0. 64. , y=7 при х=0.

65. , у=3 при х=1. 66. ,y = 6 при x = 0.

67. , y=1 при x=2. 68. ; y=1 при x= -1.

69. ; y=4 при x=1. 70. , у=4 при х=2.

71. - 80. Найдите общее решение дифференциального уравнения:

71. .72. . 73. .74. .75. .

76. .77. . 78. .79. . 80. .

81. – 90. Исследуйте на сходимость ряд:

81. .82. .83. . 84. .85. .

86. .87. . 88. . 89. . 90.

91. – 100. Задачи из основ теории вероятностей и математической статистики

91. Сколькими способами можно расставить на полке шесть различных книг?

92. Сколько пятизначных чисел можно составить из цифр 0, 1, 2, 3, 4 без повторений?

93. Из цифр 1, 2, 3, 4, 5 сколько можно составить различных двузначных чисел при условии, что ни одна

из них не повторяется?

94. В группе из 30 студентов нужно выбрать трех дежурных. Сколькими способами это можно сделать?

95. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторяется?

96. Сколько сложных красок можно составить из 7 основных, если смешивать их по 3?

97. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке.

Сколькими способами это можно сделать?

98. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна

вероятность того, что этот билет выигрышный.

99. В урне 10 белых и 5 черных шаров. Наугад вынимают два шара. Какова вероятность того, что оба вынутых шара окажутся белые?

100. В урне 4 белых и 7 черных шаров. Наугад вынимают два шара. Какова вероятность того, что оба вынутых шара окажутся белые?

Краткие вопросы теоретического материала и рекомендации к выполнениию заданий из контрольной работы:

РАЗДЕЛ 1.1. Функция одной независимой переменной. Пределы.

Вычисление пределов:

1. Непосредственное вычисление предела:

; .

2. Использование зависимостей между бесконечно малой и бесконечно большой функциями при взятии пределов:

3. Раскрытие неопределенности вида:

3.1. х→0(числитель и знаменатель функции, стоящей под знаком предела разделить на х в наименьшей степени стоящей в знаменателе и вычислить предел)

, в нашем случае делим на (х²)

3.2 х→а (числитель и знаменатель функции, стоящей под знаком предела разложить на множители, выполнить сокращение и вычислить предел)

=

3.3 Пределы иррациональных функций (под знаком предела стоит один или несколько корней): числитель и знаменатель функции, стоящей под знаком предела умножить на выражение сопряженное знаменателю или числителю (и знаменателю и числителю), выполнить действия, сократить и вычислить предел.

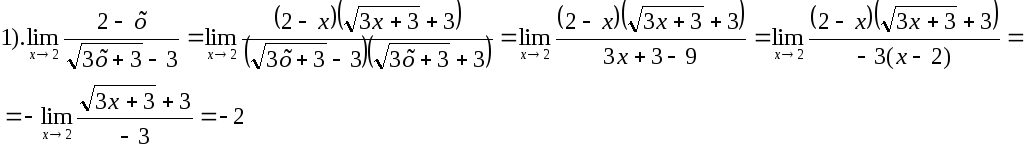
2).

3).