
ГЛАВА-2-06.13
.pdf
4. |
Если |
из условия задачи следует, что |
погрешность |
этого |
||||
приближенного равенства стремится к 0 при |
n , то искомая величина U |
|||||||
выражается определенным интегралом: |
|
|
|
|
||||
|
|
|
|
n |
b |
|
|
|
|
|
U lim f (xk ) xk |
f (x)dx |
|
|
|
||
|
|
n |
|
|
|
|
|
|
|
|
x 0 k 1 |
a |
|
|
|
||
|
|
|
|
Схема II |
|
|
|
|
1. |
Пусть |
величина |
U |
получает |
приращение |
U f (x) x , |
||
соответствующее |
изменению |
x |
на малую |
величину |
x , |
причем |
f (x) |
|
рассматривается как данная или определяемая из условий задачи функция от x .
2.Заменив приращение U дифференциалом du (главная линейная
часть приращения дифференцируемой функции) и x – дифференциалом dx ( x dx ), получим
U du f (x)dx
3. Интегрируя это равенство в пределах от x a до x b , получим
b
U f (x)dx
a
Геометрическое приложение определенного интеграла
1. Вычисление площади плоской фигуры (области (D))
а) Линии, ограничивающие область (D), заданы в декартовых координатах
Случай 1. Площадь области (D), ограниченной прямыми x a, |
x b (b>a) |
и непрерывными кривыми y f (x), y g(x), где f (x) g(x) x a;b (рис. 1), |
|
находится по формуле: |
|
b |
|
S( D) f (x) g(x) dx |
(1) |
a
119
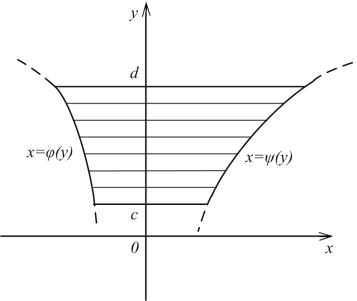
Случай 2. Площадь области (D), ограниченная прямыми y=c, y=d (d>c) и |
|
непрерывными кривыми x ( y) и x ( y), где ( y) ( y) y c;d (рис. 2), |
|
находится по формуле: |
|
d |
|
S( D) ( y) ( y) dy |
(2) |
c
Рис. 2
б) Линии, ограничивающие область (D), заданы в параметрической форме. Формула для вычитания площади области (D), ограниченной прямыми x=a, x=b (b>a), непрерывной линией, заданной параметрически уравнениями:
x (t)
y (t) и осью (ox), имеет вид:
|
t2 |
|
S( D) |
(t) '(t)dt , где a (t1 ), b (t2 ), ψ(t)≥0 t [t1;t2] |
(3) |
|
t1 |
|
в) Линии, |
ограничивающие область (D), заданы в полярной |
системе |
координат
Площадь области (D), ограниченной полярными лучами φ=α, φ=β (β>α) и непрерывными полярными кривыми: r=f(φ), r=ψ(φ), где ( ) f ( ) a; находится по формуле:
S( D) |
|
1 |
|
2 |
f |
2 |
|
(4) |
|
|
|
||||||
2 |
|
|
|
d |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120

2. Вычисление объема тела вращения
Формула для вычисления объема тела вращения, образованного вращением криволинейной трапеции вокруг оси (ox), имеет вид:
b |
|
V(ox) f 2 (x)dx |
(5) |
a |
|
(рис. 4) |
|
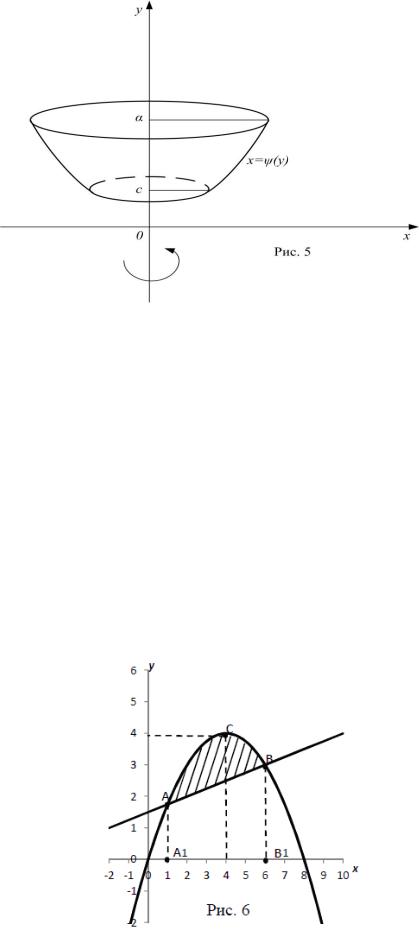
а вокруг оси (oy): |
|
|
|
V(oy) 2 ( y)dy |
(6) |
c
(рис. 5)
121
Приложение определенного интеграла к решению физических задач
1. Вычисление пути, пройденного материальной точкой при неравномерном движении по прямой со скоростью V (t) за время [t1; t2]
t2
S V (t)dt
t1
2. Вычисление работы, производимой переменной силой F(x) при перемещении по оси ox материальной точки от x=a до x=b
b
A F (x)dx
a
Примеры с решениями Пример 1. Вычислить площадь, ограниченную линиями: параболой
4 y 8x x2 и прямой 4 y x 6 .
122
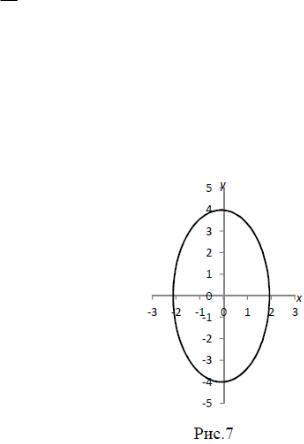
Решение. Построив данные линии, видно, что искомая площадь области ACB (рис.6) ограниченной сверху параболой и снизу прямой, которые
пересекаются в точках А (1;  ) и В (6;3), равна разности площадей А1АСВВ1 и
) и В (6;3), равна разности площадей А1АСВВ1 и
А1АВВ1. Тогда площадь области выражается интегралом в соответствии с формулой (1).
S |
|
|
1 |
6 |
((8x x2 ) (x 6))dx |
1 6 |
(7x x2 6)dx |
1 |
(7 |
x2 |
|
x3 |
6x) |6 |
|
1 |
(18 |
17 |
) 5 |
5 |
|
D |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
4 |
|
4 |
|
4 2 |
3 |
1 |
4 |
6 |
24 |
||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 5 245 кв. ед.
Пример 2. Найти площадь, ограниченную эллипсом x 2cost , |
y 4sin t . |
Решение. Оси координат совпадают с осями симметрии данного эллипса (рис. 7). Четвертую часть искомой площади S, расположенную в первой четверти координатной плоскости, найдем как площадь криволинейной трапеции, прилегающей к Ox:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
замена переменной |
|
||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
S ydx y 4sin t, x 2cost |
|
||||||
4 |
|||||||
0 |
|
x | 0 | 2 |
|
||||
|
|
dx 2sin tdt, |
|
||||
|
|
|
|||||
|
|
|
t | |
|
| 0 |
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
||
0
8 sin2 tdt
2
|
|
|
|
|
|
|
2 |
|
|
|
|
||
1 |
2 |
|
|
|||
4 (1 cos 2t)dt 4(t |
4 |
2 ; S = 4 2 кв. ед. |
||||
sin 2t) | |
||||||
2 |
2 |
|||||
0 |
0 |
|
|
|||
|
|
|
|
|
Ответ: S = 8π кв. ед.
123

Пример 3. Вычислить площадь, ограниченную кардиоидой
а сos а .
Решение. Кардиоида симметрична относительно полярной оси (рис. 8). Тогда искомая площадь равна удвоенной площади криволинейного сектора OAB. Дуга OAB описывается концом полярного радиуса ρ при изменении угла φ от 0 до π. Используя формулу (4) найдем S.
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S 2 |
d a2 сos 2 d a2 сos сos2 d |
||||||||||||||||||||||
2 |
|||||||||||||||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
2 |
|
a |
2 |
1 |
|
|
||
a |
|
( |
2sin 0 |
|
|
|
|
сos d a |
|
( |
|
sin 0 |
|
||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
a2 |
|
3 |
a2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||
Ответ: |
3 |
a2 кв.ед. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 4. Вычислить объѐм тела, образовавшегося вращением фигуры, |
|||||||||||||||||||||||
ограниченной линиями y2 |
2 px , x a вокруг оси OX (рис. 9). |
|
|||||||||||||||||||||
Решение. |
|
Построив |
|
параболу y2 2 px и |
прямую |
|
x a , |
получим |
|||||||||||||||
внутреннюю область OAB при вращении еѐ вокруг оси OX, образуется сегмент параболоида вращения. Объем этого тела находим по формуле (5).
124
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
V |
y2dx 2 pxdx px2 |0a pa2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ответ: pa2 ед. куб. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Пример 5. Определить работу, произведѐнную при адиабатическом |
||||||||||||||||||||||||||||||||||
расширении воздуха, имеющего начальный объѐм V0 = 1 м3 и давление |
P0 = |
||||||||||||||||||||||||||||||||||||
9,8·104 Па до объѐма V1 = 10 м3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Решение. |
|
Объѐм газа в закрытом сосуде и производимое им давление P |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
связаны формулой: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PV k c const, k 1,4 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть x (м) – расстояние пройденное |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поршнем (рис. 6). Предположим, что |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при изменении |
x на малую величину |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x испытываемое поршнем давление |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
остаѐтся неизменным; при этом |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
объѐм |
V изменится |
на |
V. Работа |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы |
давления |
на |
отрезке |
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выразится |
|
|
|
|
|
приближѐнным |
|||||||||||
равенством: A PS x , |
где S – площадь поршня. Так как |
PV k PV k c , то |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
P |
|
c |
, при этом V S x . Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
V k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
c |
V PV k |
V . |
(Схема II) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V k |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
V k |
|
|
|
|
|
|
|
|
|
|
|
||
Интегрируя в пределах от V0 |
до V1 |
дифференциальное равенство dA PV k |
dV |
, |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
V k |
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PV k |
|
V |
k 1 |
|
|
|
|
|
||||||||||||
|
|
|
dV |
|
|
|
V 1 k |
V1 |
PV k |
V 1 k V 1 k |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
A |
|
PV k |
|
|
|
PV k |
|
|
|
|
|
|
0 0 |
|
|
0 0 |
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
0 0 |
|
V |
|
0 0 |
1 |
k |
|
1 k |
|
1 |
0 |
|
|
|
k 1 |
|
V |
|
|
|
|
|
|
|||||||||||
|
|
V0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
V0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
9,8 104 |
1003 |
1 0,10,4 |
|
15000 кгм 147 103 (Дж) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Примеры для самостоятельного решения
Найти площадь, ограниченную линиями:
1.Параболой y=6x – x2 и осью ox
2.Параболой y=x2+4x и прямой x – y+4=0
3.Гиперболой xy=6 и прямой y=7 – x
4.Кубической параболой y=x3 и прямыми y=x, y=2x
5.Окружностью x2+y2=4x и параболой y2=2x
125

6.Лемнискатой ρ2=a2cos2φ
7.Кардиоидой ρ= a(cosφ+1)
8.Логарифмической кривой y=lnx и прямыми y=0, x = а; а > 1
9.Окружностью x2+y2=16 и параболой x2=12(y – 1)
10.Одной аркой циклоиды x=a(t – sint), y= a(t – cost) и осью абсцисс
(a=const).
Найти объѐм тела, образованного вращением фигуры, ограниченной линиями:
11.x2 y2 0, y 0, y b вокруг оси Оу a2 b2
12.y2 x 4 0, x 0 вокруг оси Оу
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||
1. 36; 2. 20 |
5 |
; 3. 17,5 – 6ln6; 4. 1,5; 5. ; 6. a 2 ; 7. |
a2 |
; 8. 1; |
9. |
16 4 3 |
|
; |
||||||||
|
2 |
|
|
|
||||||||||||
6 |
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. 3a2 ; 11. |
4 |
a2b; 12. |
34 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
3 |
15 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
§10. Несобственные интегралы
При изучении определѐнного интеграла от функции f (x) требуется, чтобы функция f (x) удовлетворяла следующим условиям:
была определена на конечном отрезке [a;b];
была непрерывна на отрезке [a;b].
Если нарушено хотя бы одно из указанных условий, то речь будет идти о
несобственных интегралах первого и второго рода.
Интегралы с бесконечными пределами
Пусть функция f (x) определена и непрерывна на промежутке [a;+ ) или (– ;a]
или (– ;+ ).
|
|
b |
Определение 1. Если существует конечный предел |
lim |
f (x)dx , то этот |
|
b a |
|
предел называется несобственным интегралом от функции f(x) на бесконечном
|
|
промежутке [a;+ ) первого рода, обозначается |
f (x)dx и в этом случае |
|
a |
126
|
|
|
|
|
|
|
b |
|
считается, что интеграл сходится. Если |
lim |
f (x)dx |
не существует или равен |
|||||
|
|
|
|
|
b a |
|
||
|
|
|
|
|
|
|
|
|
, то считается, что интеграл f (x)dx расходится. |
|
|||||||
|
|
|
a |
|
|
|
|
|
Аналогично определяются интегралы: |
|
|
|
|
|
|||
a |
|
a |
|
|
|
|
|
|
|
f (x)dx |
lim f (x)dx |
|
|
|
|
|
|
|
|
b b |
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
c |
f (x)dx |
f (x)dx |
f (x)dx |
|
lim |
|
f (x)dx |
lim f (x)dx |
|
|
|
a |
b b |
c a |
||||
Если пределы конечные, то соответствующий интеграл считают сходящимся, а если хотя бы один из пределов не существует или бесконечный, то интеграл считают расходящимся.
Интегралы от разрывных функций
1) Пусть функция y = f (x) определена и непрерывна на отрезке [a;b], а в точке x = b либо не определена, либо имеет разрыв. Такую точку x = b
будем называть особой точкой функции f (x).
|
|
b ε |
Определение 2. Если существует конечный предел |
lim |
f (x)dx , то он |
|
ε 0 |
a |
|
|
называется несобственным интегралом второго рода от функции f(x) на отрезке
b
[a;b] и обозначается символом f (x)dx . При этом говорят, что несобственный
a
b
интеграл f (x)dx сходится и записывается равенство:
a
b |
|
b ε |
f (x)dx lim |
f (x)dx . |
|
a |
ε 0 |
a |
|
||
Если конечный предел не существует или он бесконечный, то говорят, что
b
несобственный интеграл f (x)dx расходится.
a
2) Пусть функция y = f (x) определена и непрерывна на отрезке [a;b], а в точке x = a либо не определена, либо имеет разрыв. Такую точку x = a называют особой точкой функции f (x).
127

|
|
b |
|
|
|
Определение 3. Если существует конечный предел |
lim |
|
f (x)dx |
, то он |
|
ε 0 |
|
|
|||
|
a ε |
|
|
||
называется несобственным интегралом второго рода |
от функции |
f |
(x) на |
||
b
отрезке [a;b] и обозначается символом f (x)dx .
a
|
|
|
|
b |
При этом говорят, что |
несобственный |
|
интеграл f (x)dx |
|
|
|
|
|
a |
записывается равенство: |
|
|
|
|
b |
|
b |
|
|
|
f (x)dx lim |
|
f (x)dx |
|
ε 0 |
|
. |
||
a |
a ε |
|
||
Если конечный предел не существует или бесконечен, то
b
несобственный интеграл f (x)dx расходится.
a
сходится и
говорят, что
Замечание. Если функция f(x) имеет разрыв в некоторой точке x = c внутри отрезка [a;b], то по определению полагают:
b |
|
c |
|
b |
c ε |
|
|
b |
|
|
||
|
f (x)dx |
|
f (x)dx |
|
ε 0 |
|
|
|
δ 0 |
|
|
|
|
|
|
f (x)dx lim |
|
f (x)dx |
lim |
|
f (x)dx |
||||
a |
|
a |
|
c |
a |
|
|
c δ |
|
|||
при условии, что оба предела в правой части существуют, и и не зависят друг от друга. Этот интеграл также называют несобственным интегралом второго рода от функции f (x) на отрезке [a;b] и обозначается символом:
b
f (x)dx .
a
Сходимость или расходимость такого интеграла зависит от существования или не существования конечного предела.
Примеры с решениями
Пример 1. Исследовать на сходимость несобственный интеграл xe 2 xdx
1
|
Решение. |
|
|
|
|
|
|
|
|
|
|
xe 2xdx lim |
b |
|
u x |
|
du dx |
||||
|
||||||||||
|
|
|
|
|
|
|||||
|
xe 2xdx |
dV e |
2x |
dx |
V |
1 |
e |
2x |
||
1 |
b |
1 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
1 b |
|
|
|
|
|
|
|
|
e 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
2x |
|
2x |
|
|
|
|
|
b |
|
|||
lim |
|
|
e |
|
|
e |
|
lim |
|
|
|
|
||||||
2 |
|
2 |
2e |
2b |
2 |
|||||||||||||
|
b |
|
|
|
1 |
1 |
|
|
b |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b
1 e 2x
4 1
128
