
Преобразовательная техника
.pdf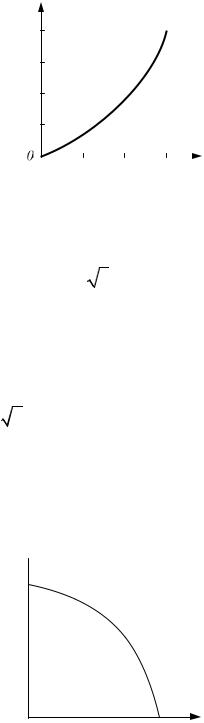
i |
= 0 или sin jectg jl + sin (l - j) = 0 . |
(2.26) |
d |
q = l |
|
Зависимость l = f (j) имеет вид, показанный на рис. 2.3. |
|
|
|
a |
|
|
2p |
|
|
1,5p |
|
|
p |
|
|
0,5p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
p j |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
3 |
|
2 |
|
|
|
|
|
|
|
|
||||
Рис. 2.3. Зависимость длительности проводящего состояния вентиля |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
от параметров нагрузки |
|
|
|
|
||||||||||||||||||||
|
Постоянная составляющая выпрямленного тока |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
Ed |
|
|
|
|
|
E2 |
(1 - cosλ), |
|
|
||||||||||||||
|
|
|
|
|
Id = |
= |
|
|
2 |
|
(2.27) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Rd |
2πRd |
|
|
|
|
|
|
|
|
|
|
|||||||||
или в относительных единицах: |
|
|
|
|
|
|
|
|
Ed* |
|
|
|
|
|
||||||||||||||||
|
|
|
Id* = |
|
Id |
= |
1 - cosλ |
tgj = |
tgj, |
(2.28) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
Id max |
2π |
|
|
|
π |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
E2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где I |
d max |
= i |
= |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
d |
R = 0 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Таким |
образом, |
последнее |
выражение |
представляет |
|
собой |
|||||||||||||||||||||||
уравнение |
|
внешней |
|
|
|
|
|
характеристики |
* |
= f (I |
* |
), |
||||||||||||||||||
|
|
|
|
|
|
выпрямителя: E |
d |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
изображенной на рис. 2.4.
Ed*
1
1 Id*
Рис. 2.4. Внешняя характеристика выпрямителя при работе на активно-индуктивную нагрузку
61

При работе выпрямителя на двигательную нагрузку, при заряде |
||||||
аккумуляторных батарей и в других случаях, когда в цепи нагрузки |
||||||
имеется |
противоЭДС, |
имеют |
место |
определенные |
особенности. |
|
Рассмотрим работу однофазного однополупериодного выпрямителя на |
||||||
двигатель постоянного тока с противоЭДС E0 (рис. 2.5). |
|
|
||||
|
|
|
e2 |
|
|
|
|
|
|
|
p |
E0 |
2p |
|
|
|
|
|
|
q |
|
id |
+ |
id |
|
|
|
U1 |
e2 |
E0 |
|
|
|
|
|
X |
- |
|
l |
|
q |
|
|
|
eх |
S |
|
|
|
|
|
y |
|
|
|
|
|
|
|
S |
|
q |
Рис. 2.5. Работа однофазного однополупериодного выпрямителя |
||||||
|
на двигательную нагрузку |
|
|
|||
Здесь X – суммарное индуктивное сопротивление в цепи вторичной обмотки трансформатора. Из-за наличия противоЭДС вентиль В откроется только в точке ψ.
Поэтому, взяв за начало координат точкуy, запишем для цепи нагрузки:
e |
- X |
did |
= E или |
|
E sin (θ + ψ)- X |
did |
= E . |
(2.29) |
||
2 |
||||||||||
|
||||||||||
|
|
|||||||||
2 |
|
dθ |
0 |
2 |
|
dθ |
0 |
|
||
|
|
|
|
|
|
|
|
|||
Решая |
это уравнение |
|
относительноi , с |
учетом |
нулевых |
|||||
|
|
|
|
|
|
d |
|
|
||
начальных условий, получаем:
i = |
2E2 |
écos y - cos(q + y)ù |
- |
E0 |
q. |
(2.30) |
|
X |
|
||||||
d |
ë |
û |
|
X |
|
||
Графическое изображение этой
рис. 2.5, в, а на рис. 2.5, г представлена функция
Постоянная составляющая тока нагрузки:
|
|
|
1 λ |
|
|
|
E |
|
|
|
|
|
|
|
2 |
éλcosψ - sin (λ + ψ) + |
|||
I |
d |
= |
|
ò |
i dθ = |
2 |
|||
|
|
||||||||
|
|
2π |
d |
2πX |
ë |
||||
|
|
|
|
0 |
|
|
|
|
|
функции представлено на
e = -X |
di |
. |
|
||
|
|
||||
x |
dθ |
|
|||
|
|
|
|||
|
E |
δ2π |
|
||
sinψù - |
|
0 |
|
|
, (2.31) |
|
|
|
|
||
û |
|
X |
|
||
|
|
|
|||
62

где δ = λ или в относительных единицах: 2π
|
|
I * |
= |
|
Id |
|
= |
1 |
élcos y - sin (l + y) + sin yù - E*d2 |
, |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
d |
|
Id max |
|
2p ë |
|
|
|
|
|
û |
|
d |
|
|
||||||||||
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
E |
|
|
|
|
E |
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
Ed* = |
|
|
|
|
2 |
|
|
|
|
|
|||||
где Id max |
E |
= 0 |
= |
|
|
2 |
; |
|
0 |
|
; Ed max = |
|
2 |
. |
|
|
|
|
|
|||||||
|
X |
|
E |
|
|
|
p |
|
|
|
|
|
||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
d max |
|
|
|
|
|
|
|
|
||||
Для установления зависимости между λ, ψ и Id воспользуемся ус- |
||||||||||||||||||||||||||
|
|
|
|
= 0 , откуда находим: cosψ - cos(λ + ψ) = |
E*λ |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
ловием: i |
|
|
d |
|
. |
|
||||||||||||||||||||
|
|
π |
||||||||||||||||||||||||
d |
q = l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|||
Связь |
между Ed* |
и |
ψ |
дает выражениеsinψ = |
Ed |
, которое |
||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
получается из исходного уравнения для этой схемы в начале координат ( q = 0 ). Таким образом, полученные выражения позволяют построить
зависимости |
|
λ = f (Id* ); ψ = f (Id* ) (рис. 2.6) и |
внешнюю характерис- |
|||||||||||||||||||
тику выпрямителя Ed* = f (Id* ) (рис. 2.7). |
|
|
|
|
|
|||||||||||||||||
l, y |
|
|
|
|
|
|
|
|
|
|
|
|
E* |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
3p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||
|
|
|
|
l |
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
p |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
1 |
Id* |
|
|
* |
|||||||||||||
|
|
|
|
|
|
|
Id |
|||||||||||||||
Рис. 2.6. Зависимость длительности проводящего состояния вентиля и угла задержки от тока нагрузки
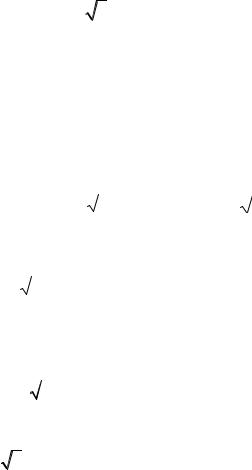
Для сглаживания пульсаций выпрямленного напряжения на выход выпрямителя параллельно нагрузке часто включают конденсаторС. Аналогичные режимы возникают и в других случаях, когда нагрузка выпрямителя имеет емкостный характер (рис. 2.8, а).
63

Из-за остаточного напряжения на конденсатореС, |
играющего |
|
|||||||||||||
роль противоЭДС, вентиль В откроется только в точке О1 с запаздыва- |
|
||||||||||||||
нием на угол φ относительно начала координат. |
|
|
|
|
|||||||||||
На |
|
интервале О1KО2 |
|
ток, |
протекающий |
через |
|
вентиль , |
В |
||||||
заряжает конденсатор С и образует ток нагрузкиid . Поэтому на этом |
|
||||||||||||||
участке |
|
|
|
|
|
|
|
|
|
2E2 sin (q + j) ; |
|
|
|
||
|
|
i |
= i |
+ i |
, i |
= e2 |
= |
|
|
|
|||||
|
|
a |
|
C |
d |
d |
|
Rd |
|
|
Rd |
|
|
|
|
|
|
|
|
= wC dUC |
|
|
|
|
|
|
|
||||
|
|
i |
|
= |
2E wCcos (θ + j). |
|
(2.32) |
|
|||||||
|
|
C |
|
|
dθ |
|
|
2 |
|
|
|
|
|
|
|
В |
точке О2 |
|
|
|
|
|
|
|
|
|
нагрузкуRd . |
|
|||
конденсатор |
начинает |
разряжаться на |
|
||||||||||||
На участке О2 KО3 |
напряжение на конденсаторе изменяется примерно |
|
|||||||||||||
так же, как и ЭДС e2 , поэтому здесь имеет место равенство id = iС + ia . |
|
||||||||||||||
|
|
|
|
|
|
|
e2 , |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
UС |
|
|
|
|||
|
|
|
|
|
|
|
UС |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
EС 0 |
|
О5 |
|
|
|
iа |
|
|
|
|
|
|
|
|
|
p |
|
|
||
|
|
|
|
|
|
|
|
О1 О2 |
О3 |
О4 |
2p |
О6 q |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
U |
e |
i |
|
С i |
|
R |
|
i |
|
|
|
Uобр max |
|
|
|
1 |
2 |
С |
|
d |
|
d |
|
|
ia |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
id |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iС |
|
q |
|
|
|
|
|
|
|
|
|
j |
|
l |
|
|
|
|
|
Рис. 2.8. Работа однофазного однополупериодного выпрямителя на активно-ёмкостную нагрузку
В точке О3 |
вентиль В закрывается( ia = 0 ), т. к. |
e2 уменьшается |
|||||||||||||||
более интенсивно, чем UС . |
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому на |
интервале О3 KО6 |
ток нагрузки |
протекает только |
||||||||||||||
благодаря разряду конденсатора С. При этом |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
- |
|
q-l-j |
|
|
|
|
|
|
|
|
|
|
U |
d |
= U |
С |
= E |
e wCRd |
, |
|
|
(2.33) |
|||
|
|
|
|
|
|
|
С0 |
|
|
|
|
|
|
|
|
||
где EC 0 – начальное напряжение на конденсаторе в точке О3 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
- |
2p-l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В точке О |
6 |
: |
U |
d |
= U |
С min |
= E |
e wCRd |
= |
2 |
E sin j. |
||||||
|
|
|
|
|
С0 |
|
|
|
|
|
2 |
|
|||||
64
Особенностью |
|
работы |
|
|
выпрямителя |
|
на |
|
|
емкостную нагрузку |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
является повышение величины обратного напряжения на вентиле: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
p-l-f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
= |
|
|
2E |
|
|
|
+ E |
|
|
|
wCR |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.34) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
обр max |
|
|
2 |
|
|
|
e |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
что необходимо учитывать при выборе |
|
|
силовых вентилей. Второй |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
важной |
особенностью |
является |
|
|
|
резкий |
|
|
|
|
скачок |
|
|
|
зарядного |
тока |
|||||||||||||||||||||||||||||||||||||||||||||
конденсатора в момент отпирания вентиля (точка О1 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
На |
практике |
|
из-за |
|
|
|
малости |
|
|
|
|
|
интервалаО KО |
3 |
|
им |
можно |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пренебречь и считать, что вентиль закрывается в точке О2 . |
|
|
π |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ + |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e - |
|
2 |
|
|
|
|
|||
Тогда |
λ = |
- j ; |
|
E |
|
= |
|
|
|
|
|
E |
|
|
; |
U |
|
|
|
= U |
|
|
|
|
|
|
|
|
E |
|
|
|
|
wCR d |
|
; |
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
d |
С |
|
|
|
2 |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
С 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π+j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
π+j |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
- |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wCRd ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wCRd . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
U |
С min |
= |
|
2 |
E e |
|
j = arcsin e |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Одним |
|
|
из |
критериев |
|
|
|
|
|
|
|
|
качества |
|
|
выпрямленного |
напряжения |
||||||||||||||||||||||||||||||||||||||||||||
является отношение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π+j |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
π + j |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( 2E2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
EС max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wСRd |
; ln k |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
= k = |
|
|
|
|
|
|
|
|
; k |
= e |
= wСRd |
; |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
E |
|
|
æ |
|
|
|
|
|
|
|
3 |
π+j |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
С min |
|
|
ç |
|
|
- |
2 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
ç |
|
|
|
|
|
|
|
wСR |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2E2e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
è |
|
|
|
|
d |
ø |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π + j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С = |
2 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.35) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wR |
ln k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.1.2. Двухполупериодная схема выпрямления со средней точкой |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эта |
|
схема |
|
|
|
представляет |
|
|
|
|
|
собой |
|
|
|
|
|
два |
|
|
однополупериодных |
||||||||||||||||||||||||||||||||||||||||
выпрямителя, работающих на общую нагрузкуRd |
и питающихся от |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
находящихся |
в противофазе |
ЭДСe2a |
и |
|
|
e2b |
|
(рис. 2.9). Для |
|
|
создания |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
этих ЭДС в схеме является обязательным наличие трансформатора Тр с двумя полуобмотками на вторичной стороне, имеющими среднюю точку.
В случае чисто активной нагрузки и с учетом допущений .п2.1.1 для рассматриваемой схемы имеют место следующие основные соотношения:
65

|
|
|
|
1 |
|
π |
|
|
|
|
|
|
|
|
2 |
|
|
|
E |
|
|
|
|
E |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
E |
|
= |
|
|
|
|
|
2E |
|
sin θdθ = |
|
2 |
; |
|
I |
|
= |
d |
; |
|
|
|
|
|
|
||||||||
d |
π |
ò |
|
|
|
|
|
d |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
π |
|
|
|
R |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
E2 |
; |
|
|
|
|
|
Id |
; |
|
|
|
|
|
|
|
|
|
|
||||||||
i |
|
= |
|
|
|
2 |
|
|
I |
|
= |
U |
|
|
|
= 2 |
|
|
E . |
(2.36) |
|||||||||||||
|
|
|
|
|
|
а ср |
обр max |
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
а max |
|
|
|
Rd |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
Поскольку мгновенное |
|
значение |
|
|
первичного |
токаi = |
|
(i |
- i |
), |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
a2 |
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kтр |
|
|
|||
то очевидно, что он представляет собой синусоиду и, следовательно,
I = |
kф |
I |
d |
, где k |
ф |
= 1,11 – коэффициент формы для синусоиды. |
||
|
||||||||
1 |
kтр |
|
|
|
|
|||
|
|
|
|
|
e2a |
e2b |
||
|
|
|
|
|
|
e2 |
||
|
|
|
p |
2p |
|
|
|
|
q |
|
В1 |
|
|
|
e2a |
|
ud |
|
|
Rd |
|
|
E |
|
U1 |
|
|
|
d |
|
|
|
q |
|
e2b |
|
|
|
|
В2 |
i2 = id |
|
|
|
|
Id |
ia1 |
ia2 |
|
|
|
q
i1
q
Рис. 2.9. Двухполупериодный выпрямитель со средней точкой
Значения мощности:
P |
= 2E |
2 |
I |
2 |
= 1,74P ; |
P = E I |
|
=1,23P ; |
|||||
2 |
|
|
|
|
|
d |
1 1 1 |
|
d |
||||
|
|
|
|
|
|
|
P |
+ P |
|
|
|
|
|
|
P |
|
|
= |
1 |
2 |
= 1,48P . |
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
расч |
|
|
2 |
|
|
d |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение между мощностями P , |
P и P объясняется теми |
||||||||||||
|
|
|
|
|
|
|
|
|
|
d |
|
1 |
2 |
же причинами, что и в однофазной однополупериодной схеме выпрямления, но в отличие от нее силовой трансформатор не имеет постоянно-
66
го подмагничивания, так как постоянные составляющие магнитных потоков обеих полуобмоток равны по величине и направлены навстречу друг другу.
При учете индуктивных сопротивлений рассеяния обмоток
æ |
|
|
|
|
1 |
|
|
ö |
|
|
силового трансформатора ç X |
a |
= X |
2 |
+ |
X |
1 |
÷ |
возникает ряд особен- |
||
2 |
||||||||||
ç |
|
|
|
÷ |
|
|||||
è |
|
|
|
|
kтр |
|
|
ø |
|
ностей в работе этой схемы выпрямления (рис. 2.10).
|
|
X a |
e2 |
e2a |
e2b |
|
|
B1 |
|
|
|
|
e |
|
ia1 |
p |
2p |
|
2a |
Rd |
|
|
q |
u1 |
|
|
|
||
|
- |
+ |
|
|
|
|
e2b |
|
ia2 |
|
g |
|
|
|
id |
|
|
|
|
|
ia1 |
ia2 |
|
|
|
X a |
B2 |
||
|
|
|
|
|
|
|
|
|
y |
|
q |
Рис. 2.10. Двухполупериодный выпрямитель со средней точкой |
|
||||||
с учетом индуктивных сопротивлений рассеяния трансформатора |
|
||||||
На интервале 0Kp открыт вентильB1 . Поскольку в цепи |
|||||||
протекания тока имеется индуктивное сопротивлениеX a , то кривая
будет затянута за точку. Вπ |
связи |
с |
этим |
вентильB2 |
не |
может |
||
открыться в точке , πтак как |
на |
сопротивленииRd |
будет |
падение |
||||
напряжения Ud = id Rd , которое |
в |
точке |
π не |
равно0 |
и |
играет роль |
||
противоЭДС в цепи вентиля B2 . |
|
|
|
|
в точке( p + y ), |
|
||
Следовательно, B2 включается |
только |
когда |
||||||
ЭДС e2b станет равной величине Ud . В момент отпирания вентиля B2 |
||||||||
вентиль B1 еще продолжает вести ток за счет энергии, накопленной на |
||||||||
интервале 0Kp в магнитном поле индуктивного сопротивления X a и в течение интервала g оказываются открытыми оба вентиля, что приводит к короткому замыканию вторичной обмотки трансформатора.
Процессы, протекающие в выпрямителе при переключении тока с одного вентиля на другой, называются коммутационными процессами, а интервал, в течение которого протекает коммутационный процесс, называется коммутационным интервалом или углом коммутации.
67

Введение в |
цепь нагрузки индуктивного |
сопротивленияX |
||
(рис. 2.11, а) приводит |
|
|
d |
|
к тому, |
что вентиль B2 включается не в точке |
|||
( p + y ), как было |
в |
случае |
на рис. 2.10, а раньше, так |
как величина |
противоЭДС в цепи вентиля B2 будет уменьшена на величину ЭДС самоиндукции сглаживающего дросселя, поддерживающую убывающий ток ia1. В пределе, если X d = ¥ , включение вентиля B2 произойдет точно в точке p . Как показывает анализ электромагнитных процессов в
выпрямителях, можно считать X d = ¥ |
, если |
X d |
= (2K3) [1]. |
|||||
Rd |
||||||||
|
|
|
|
|
|
|
||
|
|
e2 DU x |
e2a |
DU x |
e2b |
|||
X a |
B1 |
|
|
|
|
|
|
|
|
ia1 |
|
|
|
|
p |
2p |
|
e2a R |
|
|
|
|
|
q |
||
X |
d |
|
|
|
|
|
||
d |
|
|
|
|
|
|
||
U1 |
|
id |
g |
|
|
g |
|
|
e2b |
i |
|
|
|
||||
|
|
|
ia1 |
|
ia2 |
|||
|
a2 |
|
|
|
|
|||
|
|
i2k |
|
|
|
|
q |
|
X a |
B2 |
|
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
Id |
|
|
|
|
|
|
|
|
|
|
|
q |
|
Рис. 2.11. Коммутационные процессы в двухполупериодном выпрямителе со средней точкой
Рассмотрим коммутационные процессы, которые протекают, например, в точке 0 , при переходе тока с вентиля B2 на вентиль B1 при
условии |
X d = ¥ . Тогда ток id |
будет идеально сглажен (рис. 2.11, в), а |
|||||||
коммутация вентилей будет начинаться в точках 0, p, 2p, K и т. д. Эти |
|||||||||
точки |
называются точками |
естественной |
коммутации. В |
точке 0 |
|
||||
включается |
вентиль B1, |
а |
вентиль B2 , проводивший |
ток |
на |
||||
предыдущем интервале, будет по-прежнему проводить ток в течение |
|||||||||
коммутационного интервала, несмотря на приложенную немук со |
|||||||||
стороны |
|
вторичной |
обмотки |
трансформатора |
в |
запирающем |
|||
направлении |
ЭДС (e = e2a + e2b ). Такое |
положение |
будет сохраняться |
||||||
пока |
не |
израсходуется |
|
энергия, запасенная |
в |
магнитном |
поле |
||
индуктивного сопротивления X a , в цепи вентиля B2 .
68
При одновременном открытом состоянии вентилейB1 и B2
возникает |
коммутационный |
контур(рис. 2.12), для |
которого |
справедливо уравнение: |
|
|
|
|
|
|
e |
|
- X |
|
di2k |
- X |
a |
|
di2k |
+ e |
= 0 , |
|
(2.37) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
где i2k |
|
|
2a |
|
|
|
a |
dθ |
|
|
|
|
|
|
|
|
|
dθ |
2b |
|
|
|
|
||||||||
– ток коммутационного контура. Решение этого уравнения |
|
||||||||||||||||||||||||||||||
относительно i2k |
с учетом нулевых начальных условий дает |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
i |
|
|
= |
|
2 |
E2 |
(1 - cosθ). |
|
|
(2.38) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2k |
|
|
X a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
e2a |
|
|
|
|
|
|
e2b |
|
|
|
|
|
|
|
Rd |
|
|
|
|||||||||
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
X a |
|
|
|
i2k X a |
|
|
ia2 |
|
X d |
|
|
|
||||||||||||||||
|
|
|
B1 |
|
|
|
|
|
|
B2 |
|
|
|
|
|
ia1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 2.12. Коммутационный контур в схеме однофазного |
|
|||||||||||||||||||||||||||||
|
двухполупериодного выпрямителя со средней точкой |
|
|
|
|||||||||||||||||||||||||||
Графическое |
изображение |
|
этой |
|
функции |
|
представлено |
на |
|||||||||||||||||||||||
рис. 2.11, г. Очевидно, что |
|
|
ток i2k |
|
|
существует только |
на участке |
|
|||||||||||||||||||||||
коммутации |
и |
представляет |
собой |
|
ток |
вентиляB , вступающего в |
|
||||||||||||||||||||||||
работу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ток вентиля B2 |
|
|
i2k |
0Kγ = ia1 |
0Kγ . |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
i2а |
0Kγ |
= Id - ia1 |
|
|
|
. |
|
|
|
|
||||||||||||||||
Протекание тока i2k |
|
|
|
|
|
|
|
|
|
|
|
|
0Kγ |
|
|
|
|
||||||||||||||
|
в коммутационном контуре в обратном на- |
|
|||||||||||||||||||||||||||||
правлении по отношению к B2 |
следует рассматривать как уменьшение |
|
|||||||||||||||||||||||||||||
тока в |
цепи |
этого |
вентиля |
от |
|
величины |
Id , существовавшей там |
|
|||||||||||||||||||||||
в момент начала коммутации до |
|
|
0 , |
|
когда ток i2k |
достигает |
|
||||||||||||||||||||||||
величины Id . Итак, в конце коммутационного интервала i2k |
|
= Id , |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q = γ |
|
|
69

ia2 |
q = γ |
= Id - i2k |
|
q = γ |
= 0 , |
ia1 |
q = |
|
= Id , |
т. е. ток |
|
нагрузки пол- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ностью переходит на вентиль B1, а вентиль B2 закрывается. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
Из условия i2k |
|
= Id |
находим длительность коммутационного |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q = γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интервала: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
I |
|
|
X |
|
|
æ |
|
I |
|
|
X |
ö |
|||
|
|
|
|
|
2 |
|
(1 - cos γ) = Id |
; (1 - cos γ) |
|
d |
a |
|
|
d |
|||||||||||||||||
|
|
|
|
|
|
|
2 |
= |
|
|
|
; γ |
= arccos ç1 |
- |
|
|
|
a |
÷. (2.39) |
||||||||||||
|
|
|
|
X a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2E2 |
è |
|
|
|
2E2 ø |
|||||||||||
|
|
|
|
|
Совершенно аналогично коммутационные процессы будут проте- |
||||||||||||||||||||||||||
кать и в других точках естественной коммутации ( p, 2p, 3p, K). |
|||||||||||||||||||||||||||||||
|
|
|
|
|
Поскольку в течение коммутационных интервалов γ открыты оба |
||||||||||||||||||||||||||
вентиля |
|
B1 и |
B2 , |
то очевидно, |
что |
выпрямленное |
|
|
|
напряжение |
|||||||||||||||||||||
u |
d |
= |
e2a + e2b |
= 0 , |
|
так |
как e |
и |
e |
2b |
|
сдвинуты на180º |
относительно |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
друг друга. Это значит, что из кривой выпрямленного напряженияud выпадают заштрихованные участки(рис. 2.11, а), что приводит к уменьшению постоянной составляющей выпрямленного напряжения на величину DU x :
|
|
|
1 g |
|
|
|
|
|
|
|
|
I |
|
X |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
DU x = |
|
ò |
2E2 sin qdq = |
|
|
d a |
, |
|
(2.40) |
|||||||||
|
p |
|
|
p |
|||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
E2 |
|
- |
Id X a |
, |
|
|||||
E |
d |
= E |
|
- DU |
x |
2 |
(2.41) |
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
d max |
|
|
|
|
|
p |
|
|
|
p |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где Ed max – постоянная составляющая выпрямленного напряжения при
отсутствии коммутационных процессов. Последнее выражение представляет собой уравнение внешней характеристики выпрямителя
Ed = f (Id ) (рис. 2.13).
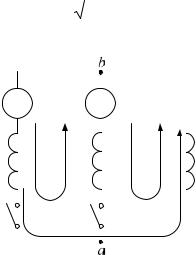
При работе двухполупериодного выпрямителя со средней точкой на противоЭДC (рис. 2.14, а) можно отметить следующие особенности:
1. В зависимости от величины X d и от величины E0 возможны три режима:
§прерывистых токов (рис. 2.14, в), когда l < p ;
§гранично-непрерывный режим (рис. 2.14, г), когда l = p ;
§режим непрерывного тока (рис. 2.14, д).
70
