6. Показательные уравнения и неравенства

6.1. Показательные уравнения

Определение 6.1. Показательными называются уравнения, у которых переменная содержится в показатели степени.

Рассмотрим основные методы решения показательных уравнений.

1. Приведение обеих частей уравнения к одинаковому основанию:

, где ,.

2. Вынесение общего множителя за скобки.

3. Уравнения, в которых правая и левая часть не приводится к одному основанию, можно решить логарифмированием:

.

4. Введение новой переменной.

5. Уравнение вида , где,,,,.

6. Показательно-степенные уравнения

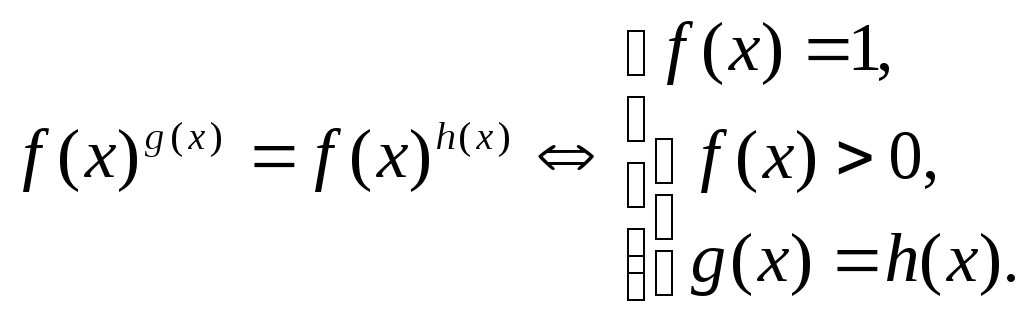
7. Функциональный метод.

Пример 6.1. Решить уравнение .

Решение.

Ответ: .

Пример 6.1. Решить уравнение .

Решение. Найдем предварительно ОДЗ уравнения:

.

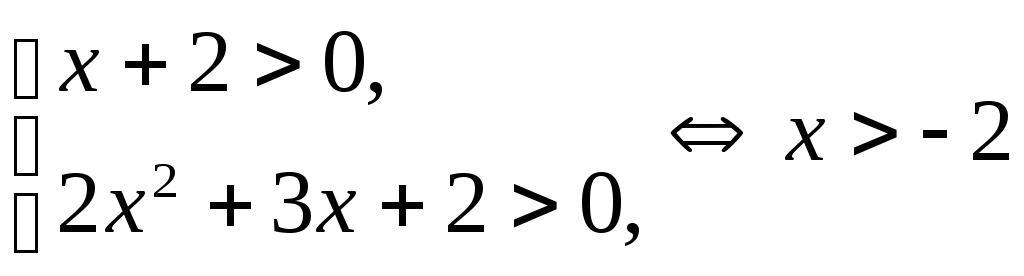Тогда на ОДЗ получим:

Оба корня принадлежат ОДЗ.

Ответ: .

Пример 6.2. Решить уравнение .

Решение. Так как левая часть является строго убывающей функцией, то любое положительное значение эта функция принимает ровно один раз. Следовательно, уравнение имеет единственное решение. Подбором получаем, что решением уравнения является .

Ответ: .

Пример 6.3. Решить уравнение .

Решение. Прологарифмируем уравнение по основанию 4:

.

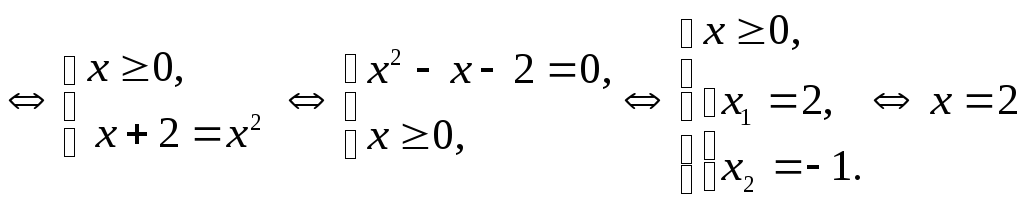Ответ: .

Пример 6.4. Решить уравнение: .

Решение. Прологарифмируем уравнение, например, по основанию 4. Тогда:

Ответ: .

Пример 6.5. Решить уравнение

.

Решение. Отметим, что

, ,.

Введем замену ,, тогда уравнение примет вид:

Сделаем замену: ,, тогда

.

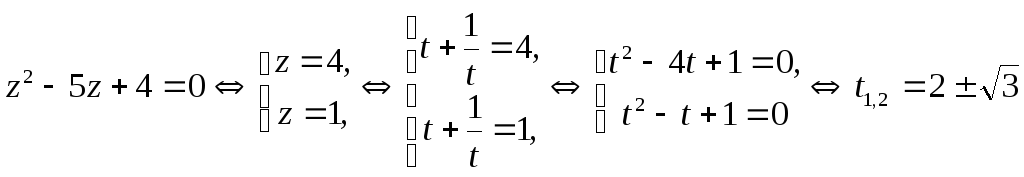Переходя обратно к переменной , получаем

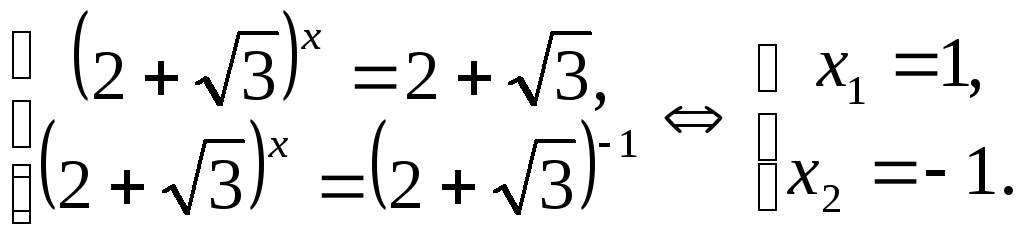
Ответ: .

Пример 6.6. Решить уравнение

Решение. Проведем предварительно преобразование правой части уравнения

.

Тогда исходное уравнение привет вид:

Ответ: .

6.2. Показательные неравенства

Решение показательных неравенств основывается на свойствах монотонности показательной функции . Напомним, что прифункция строго возрастает, а прифункция убывает.

Перечислим основные методы решения показательных неравенств.

1. Приведение обеих частей неравенства к одинаковому основанию:

;

2. Вынесение общего множителя за скобки.

3. Введение новой переменной.

4. Логарифмирование обеих частей неравенства по выбранному основанию.

5. Неравенства вида , где,,,,.

6. Неравенства вида

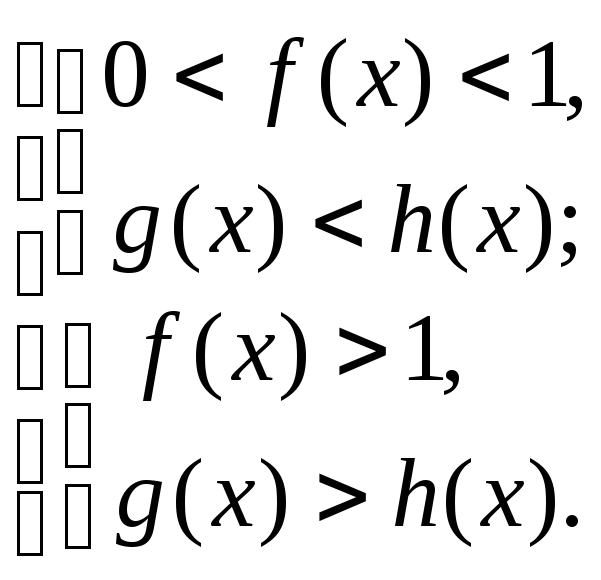
Пример 6.7. Решить неравенство .

Решение. Так как ;, то, учитывая, что основание, исходное неравенство перепишется в виде:

.

Ответ: .

Пример 6.8. Решить неравенство .

Решение. Так как основание , то

.

Ответ: .

Пример 6.9. Решить неравенство .

Решение. Так как основание , то

.

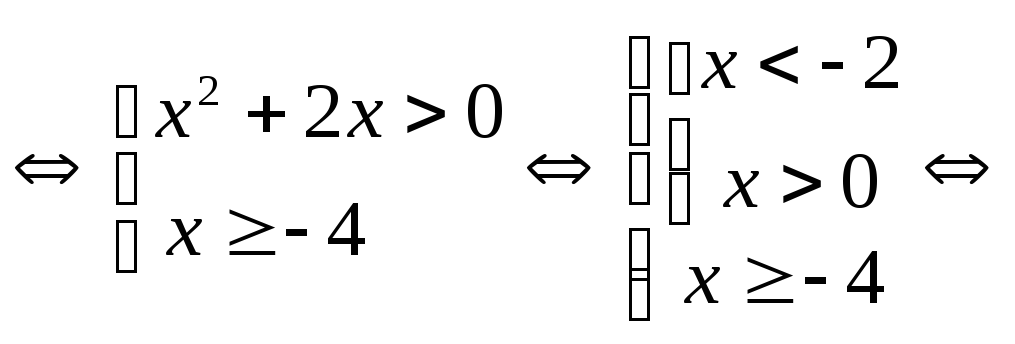
Ответ: .

Пример 6.10. Решить неравенство .

Решение.

.

Ответ: .

Пример 6.11. Решить неравенство .

Решение.

.

Ответ: .

Пример 6.12. Решить неравенство .

Решение. .

Сделаем замену ,, тогда исходное неравенство примет вид:

.

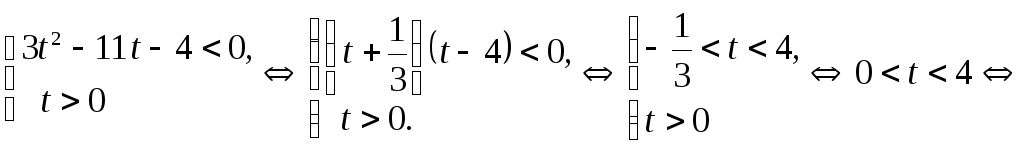
Ответ: .

Пример 6.13. Решить неравенство

Решение. .

Сделаем замену: ,, тогда

.

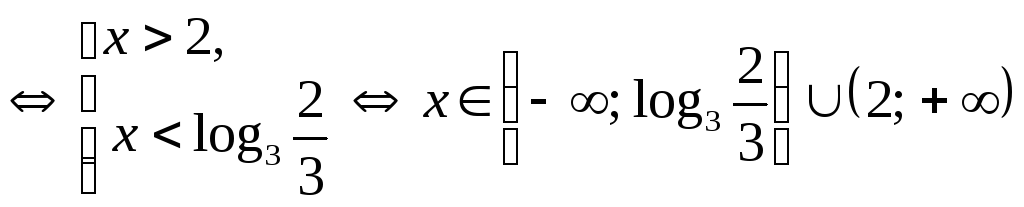Ответ: .

Пример 6.14. Решить неравенство:

Решение.

Разделим обе части неравенства на , получаем.

Сделаем замену , тогда

.

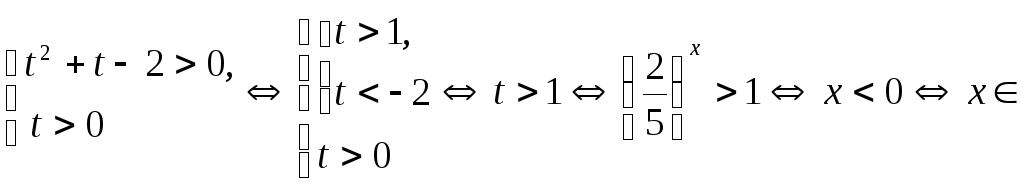
Ответ: .

Пример 6.15. Решить неравенство:

Решение: Исходное неравенство равносильно совокупности двух систем:

.

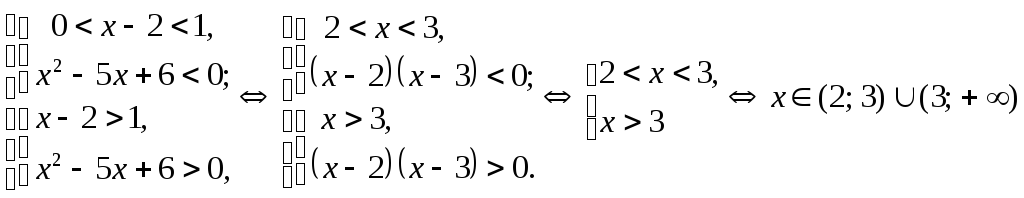Ответ: .

Пример 6.16. Решить неравенство:

Решение.

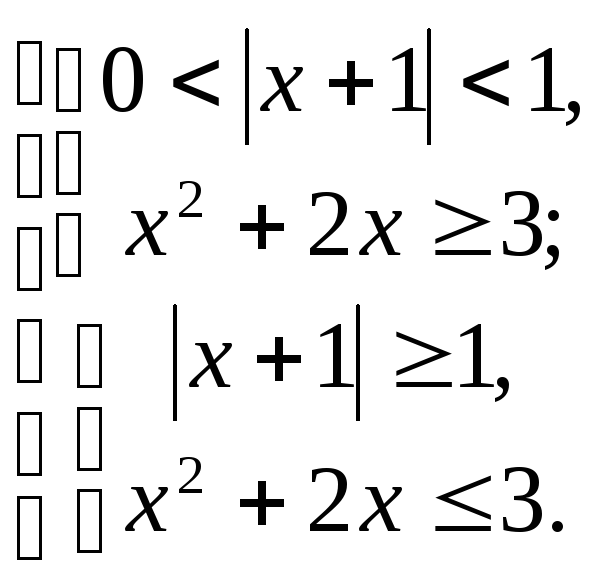
Решим первую систему полученной совокупности:

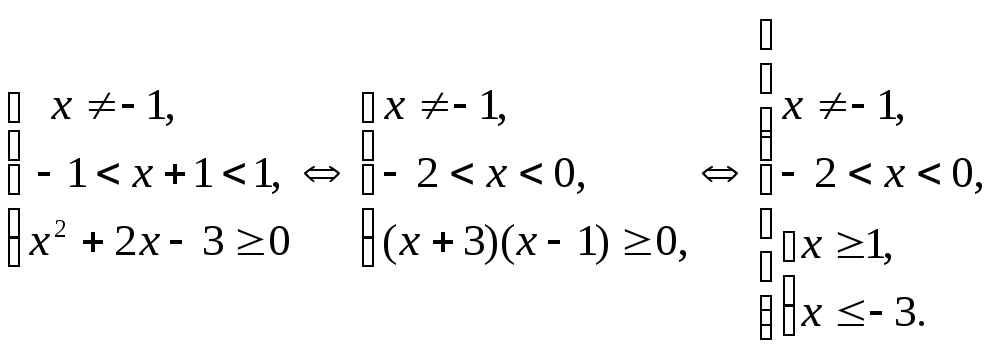
Данная система решений не имеет.

Решим вторую систему совокупности:

.

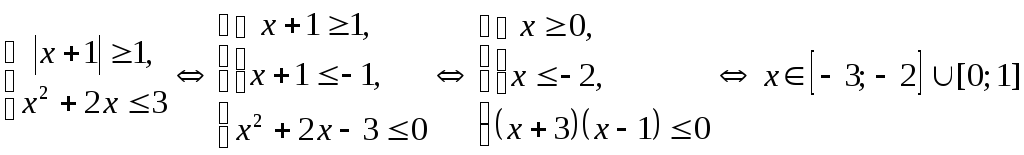Ответ: .

Пример 6.17. Решить неравенство .

Решение.

.

.

Последнее неравенство равносильно совокупности двух систем:

1.

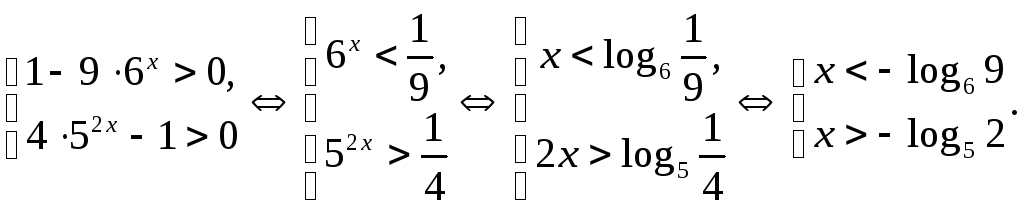
2.

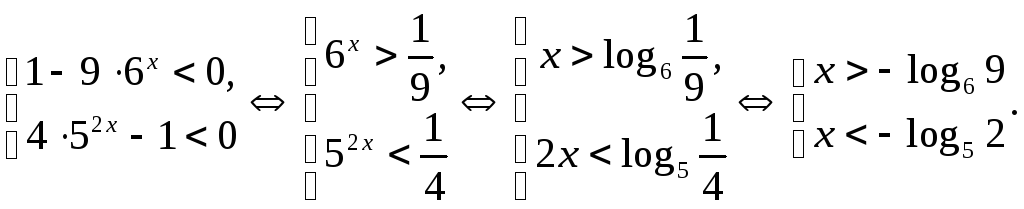
Сравним числа и. Так как, а, то, значит. Тогда получаем, что первая система решений не имеет, а решением второй служит промежуток.

Ответ: .

Пример 6.18. Решить неравенство: .

Решение. Область определения неравенства определяется условием . Исходное неравенство равносильно совокупности:

.

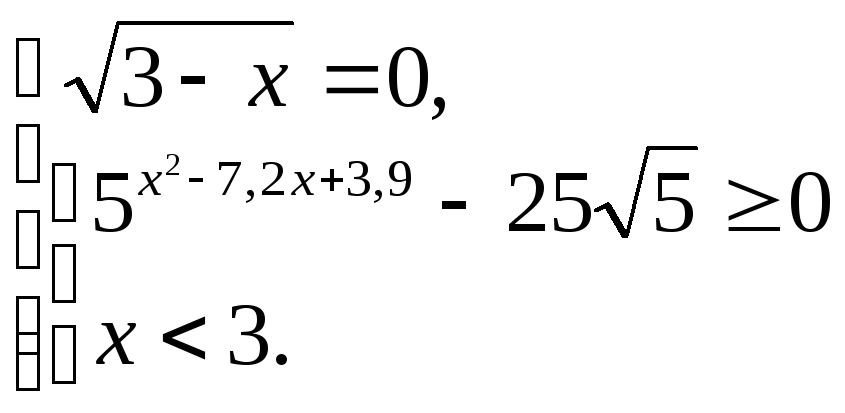Из уравнения получаем.

Так как , то первое неравенство системы можно записать в виде

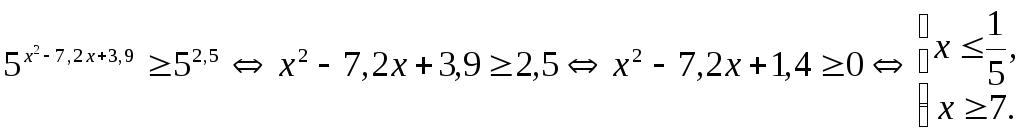
Учитывая условие , получаем решение системы – промежуток. Тогда решение исходного неравенства имеет вид.

Ответ: .

Пример 6.19. Решить неравенство

Решение. .

Сделаем замену , тогда

.

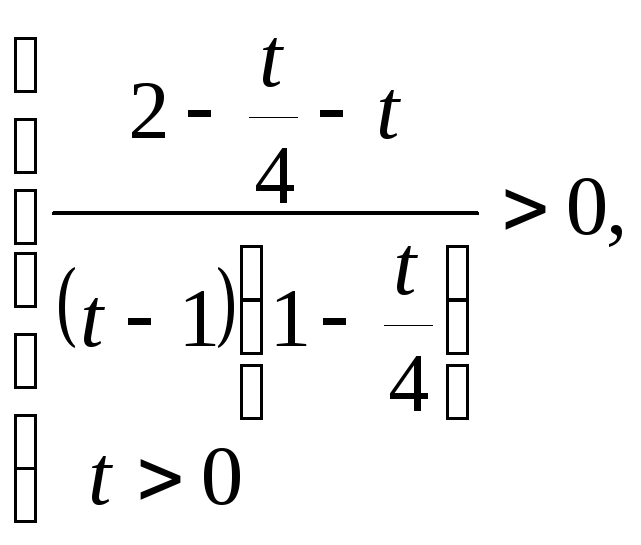
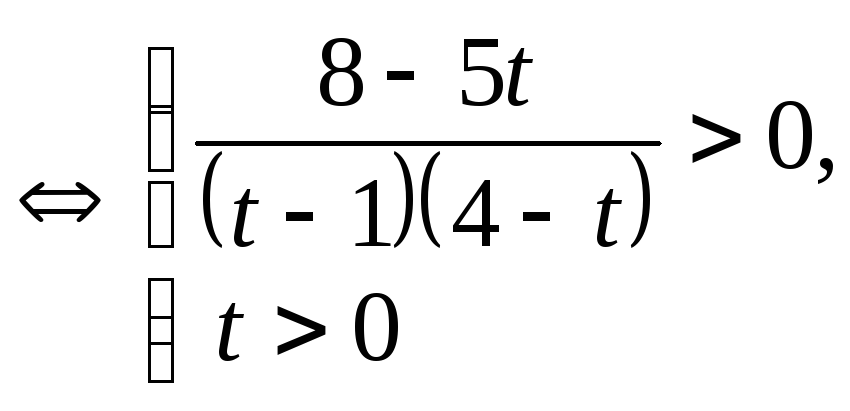
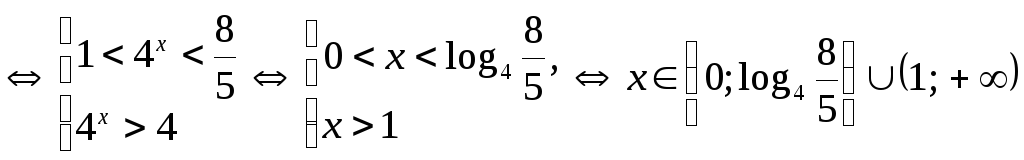Ответ: .