
Лекция дискрет 02
.pdf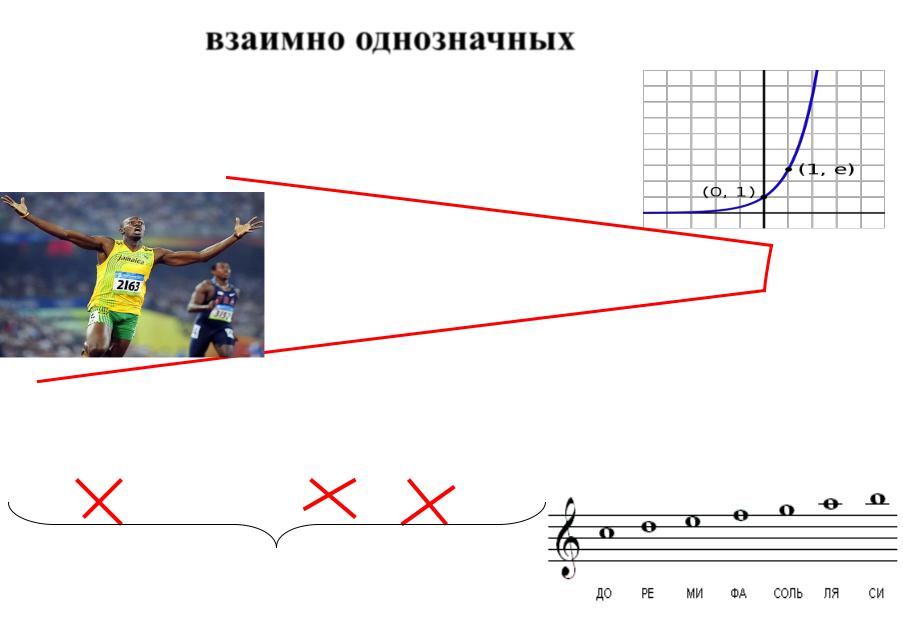
Примеры взаимно однозначных соответствий:
Любая экспонента – взаимно однозначное соответствие между R и R+
Жеребьёвка участников забега (если все номера выданы)
Представление n-мерными двоичными векторами подмножеств n-элементного множества
До – Ре – Ми – Фа – Соль – Ля - Си
(1011001)

Примеры соответствий, не являющихся взаимно однозначными:
Любая парабола (график чётной степени) не является взаимно однозначным соответствием между R и R+ - нет инъективности
Азбука Морзе – не обеспечена сюръективность – есть незадействованные сочетания точек и тире
База данных оператора связи – нет однозначности при поиске номера телефона по имени владельца

Пример взаимно однозначного соответствия
M = { m1, m2,…,mn-1,mn } – конечное множество
B (M) – булеан множества М – множество всех его подмножеств
Bn={σ = (σ1,σ2,…,σn): σi {0,1}, i=1…n } множество двоичных n- мерных векторов
Соответствие Г: B (M) Bn: каждому подмножеству
множества М = { m1,m2,...,mn } сопоставляем двоичный вектор длины n по следующему правилу:
Mj |
= {m1 |
m2 |
m3 |
m4 |
m5 |
m6 |
m7 |
m8 |
…. mn-1 mn} |
k |
|
|
|
|
|
|
|
|
|
σj = ( 0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 …. 0 1 ) |
||
k |
|
|
|
|
|
|
|
|
|
|
Вспомните |
|
до – ре – ми – фа – соль – ля - си |
||||||
|
пример: |
|
1 |
0 |
1 |
1 |
0 |
0 1 |
|
Всюду определённость |
Так как для любого подмножества Mj |
|
соответствия Г: B (M) Bn |
процедура задаёт соответствующий |
k |
|
||
|
ему вектор σj |
|
|
k |
|
Сюръективность |
Так как каждый вектор σj по |
|
соответствия Г: B (M) Bn |
k |
|
построению соответствует какому- |
|
|
либо подмножеству Mjk
Функциональность |
1) Образ любого подмножества Mj |
k |
не может |
соответствия Г: B (M) Bn |
|
|
|
быть пустым в силу всюду определённости |
|||
|
соответствия Г: B (M) Bn |
|
|
2) Допустим, для некоторого Mj |
образ содержит два различных вектора |
|||||||||||
σj |
|
|
|
|
|
k |
|
|
|
|
|
|
|
и σj . Вектора различны, значит хотя бы для одного значения i |
|||||||||||
|
k |
k |
|
|
|
|
|
|
|
|
|
|
σ |
σ , то есть одна из них равна 1, другая – 0. А это означает, что для |
|||||||||||
i |
|
i |
|
|
|
|
|
|
|
|
|
|
элемента mi одновременно имеет место mi M |
jk |
и mi M |
, что |
|||||||||
невозможно. |
|
|
|
|
|
|
|
jk |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||||
Инъективность |
|
|
|
1) Прообраз любого вектора σj не может |
||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
соответствия Г: B (M) Bn |
быть пустым в силу сюръективности |
|||||||||||
соответствия Г: B (M) Bn |
||||||||||||
|
|
|
|
|
|
|||||||
2) Допустим, для некоторого σj |
прообраз содержит два различных |
|||||||||||
подмножества Мj |
и Мj |
|
. |
k |
|
|
|
|
|
|||
|
Подмножества различны, значит хотя бы для |
|||||||||||
|
|
k |
|
k |
|
|
|
|
|
|
||
одного значения i m M |
и m M (или наоборот). Но в векторе |
|||||||||||
|
|
|
i |
|
jk |
i |
jk |
|
|
|
|
|
σj |
|
|
|
|
|
|
|
|
||||
им соответствует одно и то же значение координаты σi, значит |
||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
предположение об одновременности m M и m M противоречит |
||||||||||||
|
|
|
|
|
|
|
i |
|
i |
|
|
|
определению соответствия Г: B (M) B jk |
|
|
jk |
|
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|

Задано соответствие GА В. Если при этом соответствие H B A таково, что
(a, b) G  (b, a) H,
(b, a) H,
то соответствие H называется обратным к G и обозначается G -1
Если соответствие, обратное к заданной функции f: A B, является функциональным, то оно называется функцией, обратной к f, и обозначается f -1
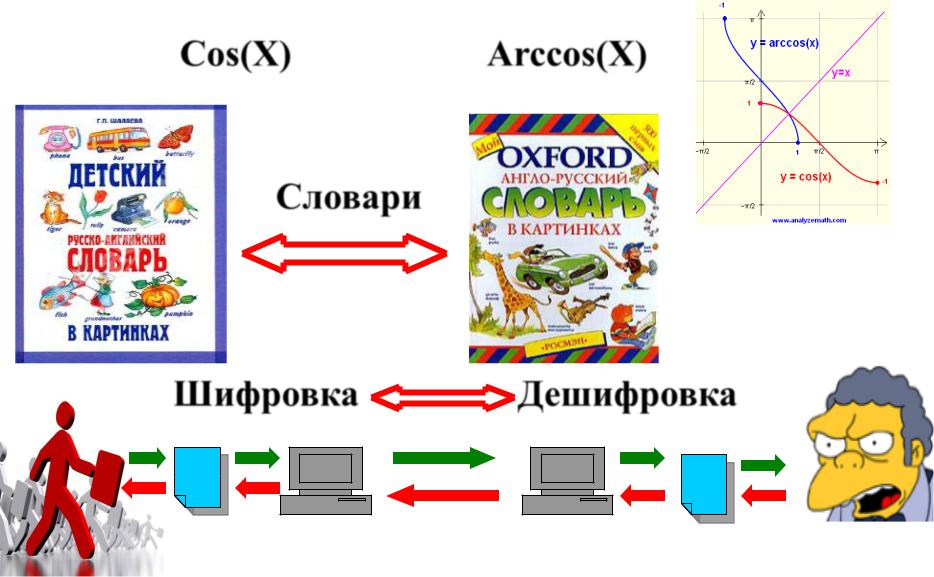
Примеры обратных соответствий
Cos(X)  Arccos(X)
Arccos(X)
Словари
Шифровка Дешифровка

Пример обратного соответствия
Было построено соответствие Г: B (M) Bn, которое
каждому подмножеству множества М = { m1,m2,...,mn } сопоставляет двоичный вектор длины n (σ1,σ2,…,σn)
Г B (M) × Bn
Обратное соответствие : Bn B (M) каждому
двоичному вектору (σ1,σ2,…,σn) сопоставляет некоторое подмножество множества М = { m1,m2,...,mn }
Bn × B (M)
От противного, аналогично тому, как была доказана взаимная однозначность соответствия Г: B (M) Bn, можно доказать
(Mj , j ) Г B (M) × Bn ( j , Mj ) |
Bn × B (M) |
|
k k |
k k |
|

Th.1.2.1 Для функции f: A B существует обратная функция g: B A тогда и только тогда, когда f является взаимно однозначным соответствием между своей областью определения и областью значений
Доказательство Th.1.2.1
Для функции f: A B существует обратная функция g: B A, значит, А = А и В = В, иначе хотя бы одна из f и g не была функциональной. Отсюда - всюду определённость и сюръективность соответствия f.
По условию f – функция, т.е. соответствие f – функционально. Но так как g – также функция, будет выполнено и требование единственности прообраза для соответствия f, то есть инъективность.
Выполнены все четыре требования, значит, f является взаимно однозначным соответствием между А и В.

f - взаимно однозначное соответствие между А и В, поэтому оно инъективно, т.е. прообразом любого элемента из В является единственный (т.е. ровно один) элемент из А.
Благодаря этому, соответствие g: B A однозначно (функционально), т.е. g: B A - функция
Доказано Th.1.2.1
