Примеры.

1. Составить уравнения касательной и нормали к графику функции у = tg²x в точке с абсциссой x₀=π/4.

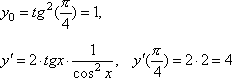
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4x – π + 1.

Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4·x + π/16 + 1.

2. Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2)² + 5 в точке M(2; 5).

y'= x – 2, y'(2) = 0 . Следовательно, касательная параллельна оси Ox, а значит ее уравнение y= 5 . Тогда нормаль параллельна оси Oy и имеет уравнение x= 2 .

3. Найти уравнение касательной и нормали к эллипсу  в точке M(2; 3).

Найдем y' по правилу дифференцирования неявной функции .

Уравнение касательной: ,т.е. .

Уравнение нормали: , т.е. .

4. Составить уравнения касательной и нормали к циклоиде x= t – sin t, y= 1 – cos tв точке М(x₀; y₀), которая соответствует значению параметра t = π/2.

При t=π/2x₀= π/2 – 1, y₀=1.

.

Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.

Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.

Теоремы о дифференцируемых функциях

Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c Î (a; b), в которой f'(c) = 0.

Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть 

Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f'(x)=0при всех x Î [a; b] .

Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.

Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что

Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:

Но неравенства f'(c) ≤ 0 и f'(c) ≥ 0 одновременно возможны лишь в случае, когда

f'(c)=0. Теорема доказана.

Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает осьOx в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a < c < b, в которой касательная параллельна оси Ox. Заметим, что доказанная теорема останется справедливой, если предположить, что на концах отрезка функция принимает равные значения f(a)=f(b), не обязательно равные нулю. Кроме того, отметим, что если внутри [a; b] найдется хотя бы одна точка, в которой производная функции f(x) не существует, то утверждение теоремы может оказаться неверным. Пример. Функция  непрерывна на [–1; 1], обращается в нуль на концах отрезка. Но производная  не обращается в нуль ни в одной точке этого отрезка. Теорема Лагранжа. Если функция y= f(x) непрерывна на [a; b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a; b] найдется хотя бы одна точка c, a<c<b такая, чтоf(b) – f(a)=f'(c)(b – a). Доказательство. Обозначим  и рассмотрим вспомогательную функцию F(x) = f(x) – f(a) – k(x – a). Выясним геометрический смысл введенной функции. Для этого рассмотрим график данной функции на [a; b] и напишем уравнение хорды АВ. Заметим, что угловой коэффициент хорды и она проходит через точку A(а; f(a)). Следовательно, ее уравнение y = f(a) + k(x – a). Но F(x)=f(x)–[f(a)+k(x–a)]. ПоэтомуF(x) при каждом x есть разность ординат графика y= f(x) и хорды, соответствующих точкам с одинаковой абсциссой. Легко видеть, что F(x) непрерывна на [a; b] , как разность непрерывных функций. Эта функция дифференцируема внутри [a; b] иF(a)=F(b)=0. Следовательно, к функции F(x) можно применить теорему Ролля. Согласно этой теореме найдется точка c Î (a; b), чтоF'(c)=0. Но F '(x) = f'(x) – k, а значит,F'(c) = f'(c) – k = 0. Подставляя в это равенство значение k, получим , что и требовалось доказать.

Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y=f(x), удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили, отношение для хорды AB, а f'(c) есть угловой коэффициент касательной. Следовательно, теорема утверждает, что на графике функции y=f(x)найдется хотя бы одна точка, в которой касательная к графику параллельна хорде, соединяющей концы дуги.

Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g'(x) ≠ 0 при всех x Î (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c Î (a; b), что .

Доказательство.Определим число . Заметим, что g(b) – g(a) ≠ 0, т.к. в противном случае выполнялось бы равенство g(b)=g(a) и по теореме Ролля в некоторой точкеd Î (a; b)g'(d) = 0. Это противоречит условию теоремы.

Составим вспомогательную функцию.

F(x) = f(x) – f(a) – k[g(x) – g(a)].

Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F'(c) = 0. Но

F'(x) = f'(x) – k·g(x), а значит F'(c) = f'(c) – k·g'(c) = 0,

откуда.

Заметим, что теорему Коши нельзя   доказать, применяя теорему Лагранжа к числителю и знаменателю дроби k. Объясните почему.

Ранее мы познакомились с примерами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытия неопределенностей вида 0/0 и ∞/∞. Сейчас рассмотрим новое правило раскрытия этих неопределенностей.

Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть или . Тогда, если существует предел отношения производных этих функций , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти . Этот предел существует . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1^∞, 1⁰, ∞⁰ нужно прологарифмировать данную функцию и найти предел ее логарифма.

Примеры.

1. .

2. .

3. .

4. 

5. 

Обозначим .

Прологарифмируем это равенство . Найдем .

Так как lny функция непрерывная, то . Следовательно,  или .

ФОРМУЛА ТЕЙЛОРА

Пусть функция y= f(x) задана на (a, b) и x₀  (a, b). Поставим следующую задачу: найти многочлен P(x), значения которого в окрестности точки x₀ приближенно совпадали бы со значениями функции f(x) в соответствующих точках. Тогда можно будет считать, что f(x)≈P(x) и задачу вычисления значенийf(x) в окрестности точки x₀ можно заменить более легкой задачей вычисления значений P(x).

Пусть искомый многочлен имеет степень n P(x) = P_n(x). Будем искать его в виде

(1)

В этом равенстве нам нужно найти коэффициенты .

Для того чтобы этот многочлен был "близок" к функции f(x) потребуем выполнения следующих равенств:

Пусть функция y= f(x) имеет производные до n-ого порядка. Найдем коэффициенты  многочлена P_n(x) исходя из условия равенства производных.

Введем обозначение n! = 1·2·3…n, 0! = 1, 1! = 1.

Подставим в (1) x = x₀ и найдем , но с другой стороны . Поэтому 

Далее найдем производную  и вычислим  Следовательно, .

Учитывая третье условие и то, что

,

получим , т.е. .

Далее . Значит, , т.е. .

Очевидно, что и для всех последующих коэффициентов будет верна формула 

Подставляя найденные значения коэффициентов  в формулу (1), получим искомый многочлен:

Обозначим  и назовем эту разность n-ым остаточным членом функции f(x) в точке x₀. Отсюда  и, следовательно,  если остаточный член будет мал.

Оказывается, что если x₀  (a, b) при всех x  (a, b) существует производная f ⁽ⁿ⁺¹⁾(x), то для произвольной точки x  (a, b) существует точка, лежащая между x₀ и x такая, что остаток можно представить в виде:

Это так называемая формула Лагранжа для остаточного члена.

Формула

 где x  (x₀, x) называется формулой Тейлора.

Если в этой формуле положить x₀ = 0, то она запишется в виде

где x  ( x₀, x). Этот частный случай формулы Тейлора называют формулой МакЛорена.

.