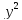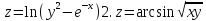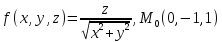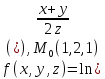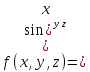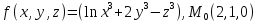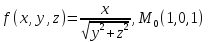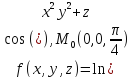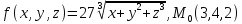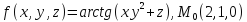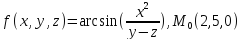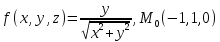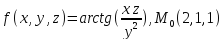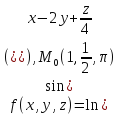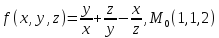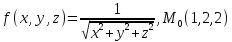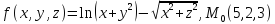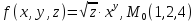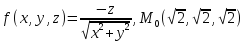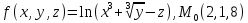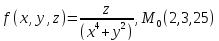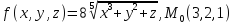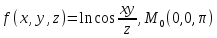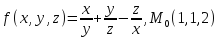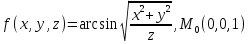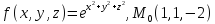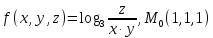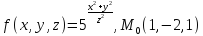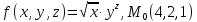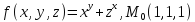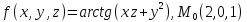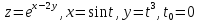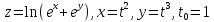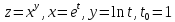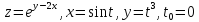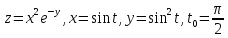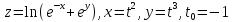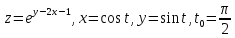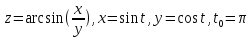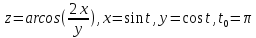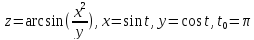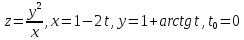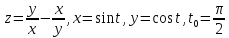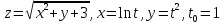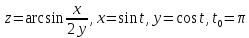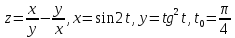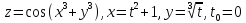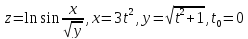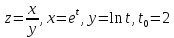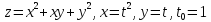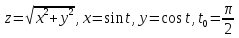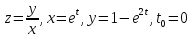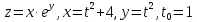- •Дифференциальное исчисление функции одной переменнойи нескольких переменных
- •Общие методические указания
- •Функция. Способы задания функции. Основные элементарные функции.
- •Предел и непрерывность функции.
- •Производная и дифференциал функции одной переменной.
- •Физические приложения производной.
- •Производная сложной функции.
- •Производные показательных и логарифмических функций.
- •Производные высших порядков
- •Производные неявной функции.
- •Касательная и нормаль к плоской кривой. Угол между двумя кривыми.
- •Дифференциал функции.
- •Исследование функций и построение их графиков
- •Индивидуальные задания. Задание1
- •Задание 2
- •Задание 3.
- •Задание 4.
- •Задание 5
- •Задание 8.
- •Задание 9.
- •Задание 10.
- •Задание 11.
- •2.Функции нескольких переменных.
- •Частные производные. Производная по направлению. Градиент.
- •Частные производные высших порядков.
- •Экстремум функции двух переменных
- •Условный экстремум
- •Расчетные задания.
Расчетные задания.
Задание 1.
Найти область определения указанных функций и частные производные.
z=
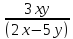 2.
z=arcsin (x-y)
2.
z=arcsin (x-y)
3.
z=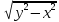 4. z=
4. z=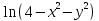
5.
z=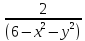 6.
z=
6.
z=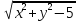
7.
z=arccos (x+y)
8. z=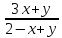
9.
z=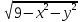 10. z=
10. z=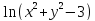
11.
z=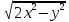 12. z=
12. z=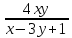
13.
z=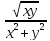 14. z=arcsin
14. z=arcsin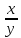
15.
z=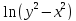 16. z=
16. z=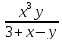
17. z=arccos (x+2y) 18. z= arcsin (2x-y)
19.
z=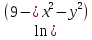 20. z=
20. z=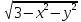
21.
z=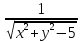 22. z=
22. z=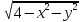
23.
z=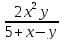 24.
z=
24.
z=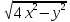
25.
z=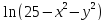 26. z= arcsin (3x-y)
26. z= arcsin (3x-y)
27.
z=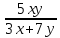 28.
z=
28.
z=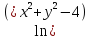
29.
z=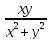 30.
z=
30.
z=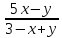
Задание 2.
Дана функция z=
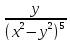 . Показать, что
. Показать, что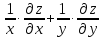 =
=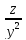
Дана функция z=х
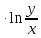 .
Показать, что
.
Показать, что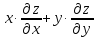 =z
=zДана функция z=(
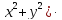 tg
tg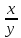 .
Показать, что
.
Показать, что
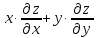 =2z
=2zДана функция z=arcsin
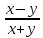 .
Показать, что
.
Показать, что
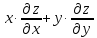 =0
=0Дана функция z=
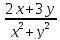 .
Показать, что
.
Показать, что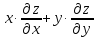 =-z
=-zДана функция z=
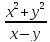 .
Показать, что
.
Показать, что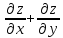 =
=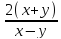
Дана функция
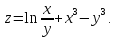 Показать, что
Показать, что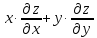 =3(
=3(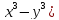
Дана функция z
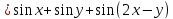 .
Показать, что
.
Показать, что
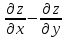 =
=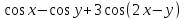
Дана функция
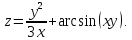 Показать, что
Показать, что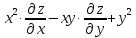 =0
=0Дана функция
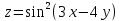 .
Показать, что
.
Показать, что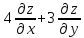 =0
=0Дана функция
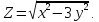 Показать,
что 3у
Показать,
что 3у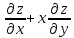 =0
=0Дана функция
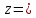 tg
tg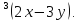 Показать,
что 3у
Показать,
что 3у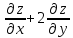 =0
=0Дана функция
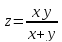 .
Показать, что
.
Показать, что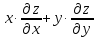 =z
=zДана функция
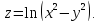 Показать, что
Показать, что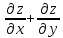 =
=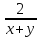
Дана функция
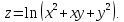 Показать, что
Показать, что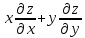 =2
=2Дана функция
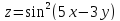 .
Показать, что
.
Показать, что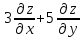 =0
=0Дана функция
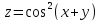 .
Показать, что
.
Показать, что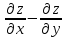 =0
=0Дана функция
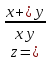 .
Показать, что
.
Показать, что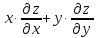 =-z
=-zДана функция
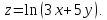 Показать, что
Показать, что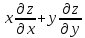 =1
=1Дана функция
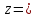 arc
arc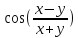 .
Показать, что
.
Показать, что
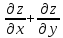 =-
=-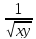
Дана функция
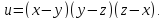 Показать, что
Показать, что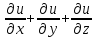 =0
=0Дана функция
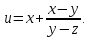 Показать,
что
Показать,
что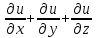 =1
=1Дана функция
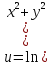 ).
Показать, что
).
Показать, что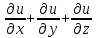 =2
=2Дана функция
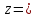 у
у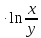 .
Показать, что
.
Показать, что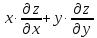 =z+2у
=z+2уДана функция
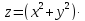 tg
tg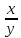 . Показать, что
. Показать, что
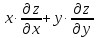 =2z
=2zДана функция
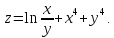 Показать,
что
Показать,
что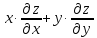 =4(
=4(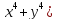
Дана функция
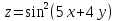 .
Показать, что
.
Показать, что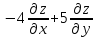 =0
=0Дана функция
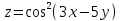 .
Показать, что
.
Показать, что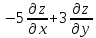 =0
=0Дана функция
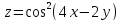 .
Показать, что
.
Показать, что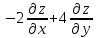 =0
=0Дана функция
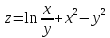 .
Показать, что
.
Показать, что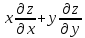 =2(
=2(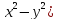
Задание 3.
Найти частные производные и частные дифференциалы следующих функций
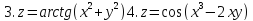
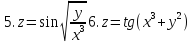
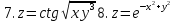
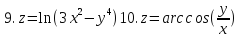
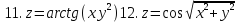
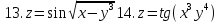
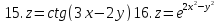
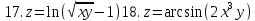
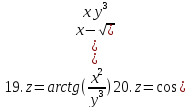
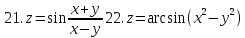
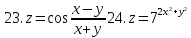
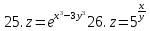
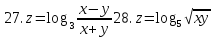
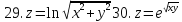
Задание 4.
Вычислить
значения частных производных f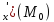 ,
f
,
f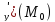 ,
f
,
f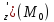 для данной функции f(х,у,z)
в точке
для данной функции f(х,у,z)
в точке
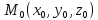
Задание 5.
Найти полные дифференциалы указанных функций
1.
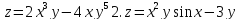
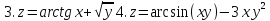
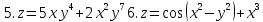
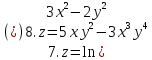
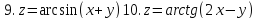
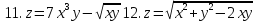
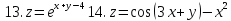
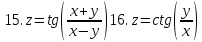
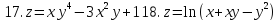
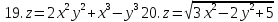
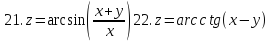
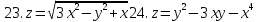
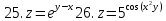
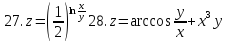
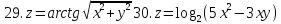
Задание 6.
Вычислить
значение производной сложной функции
z=z(х,у)
где
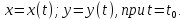
Задание 7.
Вычислить
значения частных производных функции
z(х;у),
заданной неявно, в данной точке
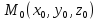
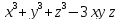 =4
=4
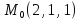
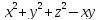 =2
=2
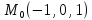
3х-2у+z=хz+5
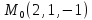
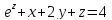
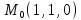
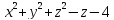 =0
=0
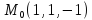
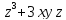 +3у=7
+3у=7
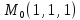
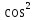 х+
х+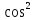 у+
у+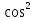 z=
z=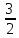
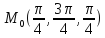
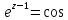 х
х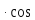 у+1
у+1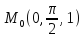
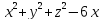 =0
=0
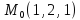
ху=
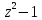
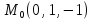
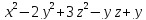 =2
=2
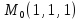
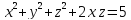
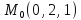
х
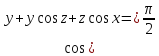
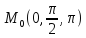
3
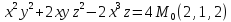
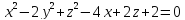
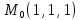
х+у+z+2=хуz
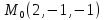
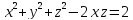
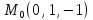
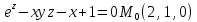
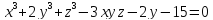
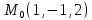
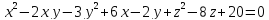
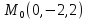
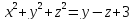
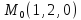
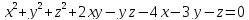
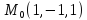
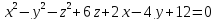
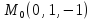
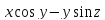 =
=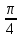
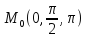
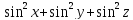 =
=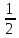
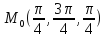
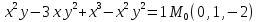
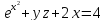
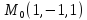
cos (ху)+ cos (хz)-sin (уz)=1
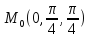
(
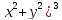 +
+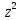 =2
=2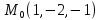
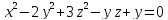
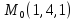
Задание 8.
Найти
уравнения касательной плоскости и
нормали к заданной поверхности S
в точке
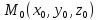
S:
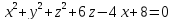
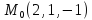
S:
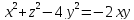
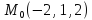
S:
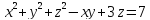
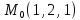
S:
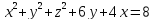
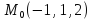
S:
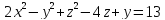
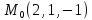
S:
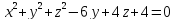
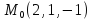
S:
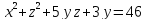
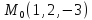
S:
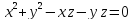
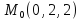
S:
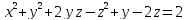
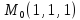
S:
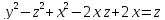
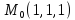
S:
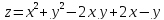
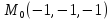
S:
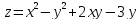
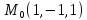
S:
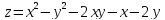
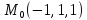
S:
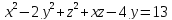
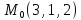
S:
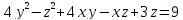
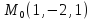
S:
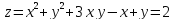
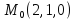
S:
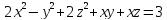
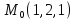
S:
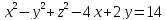
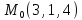
S:
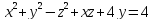
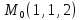
S:
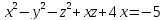
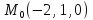
S:
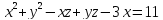
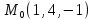
S:
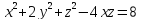
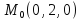
S:
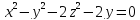
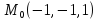
S:
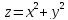
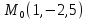
S:
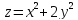
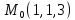
S:
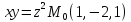
S:хуz=8
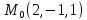
S:
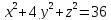
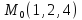
S:
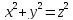
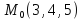
S:
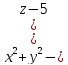
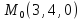
Задание 9.
Найти
градиент следующих функций в данной
точке
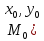 )
)
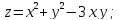
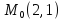
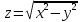 ;
;
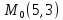
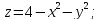
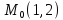
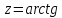
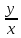 ;
;
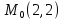
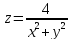 ;
;
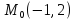
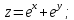
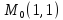
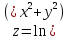 ;
;
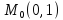
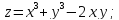
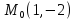
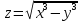 ;
;
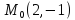
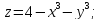
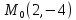
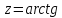
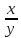 ;
;
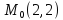
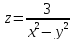 ;
;
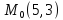
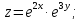
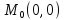
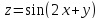 ;
;
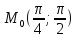
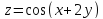 ;
;
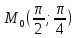
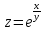 ;
;
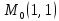
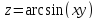 ;
;
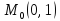
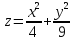 ;
;
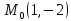
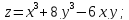
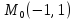
z=2ху-4х-2у ;
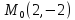
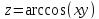 ;
;
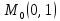
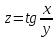 ;
;
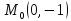
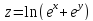 ;
;
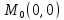
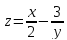 ;
;
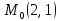
z=3 -
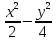 ;
;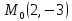
z=у
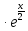 ;
;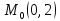
z=
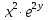 ;
;
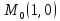
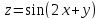 ;
;
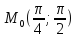
z=
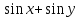 ;
;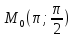
z=ctg
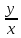 ;
;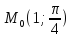
Задание 10.
Исследовать на экстремум следующие функции
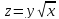 -2
-2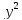 -х+14у
-х+14у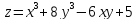
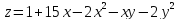
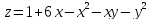
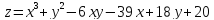
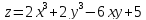
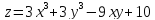
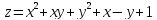
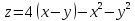
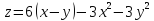
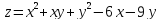
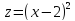 +2
+2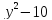
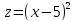 +
+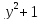
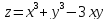
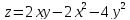
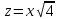 -
-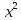 -у+6х+3
-у+6х+3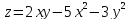 +2
+2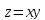 (12-х-у)
(12-х-у)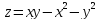 +9
+9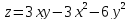
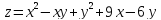 +20
+20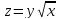 -
-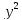 -х+6у
-х+6у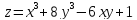
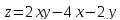
z=
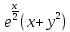
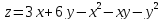
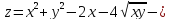 2у+8
2у+8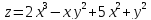
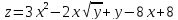
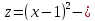 2
2