
- •Дифференциальное исчисление функции одной переменнойи нескольких переменных
- •Общие методические указания
- •Функция. Способы задания функции. Основные элементарные функции.
- •Предел и непрерывность функции.
- •Производная и дифференциал функции одной переменной.
- •Физические приложения производной.
- •Производная сложной функции.
- •Производные показательных и логарифмических функций.
- •Производные высших порядков
- •Производные неявной функции.
- •Касательная и нормаль к плоской кривой. Угол между двумя кривыми.
- •Дифференциал функции.
- •Исследование функций и построение их графиков
- •Индивидуальные задания. Задание1
- •Задание 2
- •Задание 3.
- •Задание 4.
- •Задание 5
- •Задание 8.
- •Задание 9.
- •Задание 10.
- •Задание 11.
- •2.Функции нескольких переменных.
- •Частные производные. Производная по направлению. Градиент.
- •Частные производные высших порядков.
- •Экстремум функции двух переменных
- •Условный экстремум
- •Расчетные задания.
2.Функции нескольких переменных.
Если
любой упорядоченной паре чисел
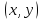 из некоторого числового множества
из некоторого числового множества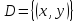 поставлено в соответствие согласно
некоторому правилу
поставлено в соответствие согласно
некоторому правилу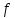 число
число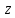 из множества
из множества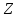 ,
то говорят, что на множестве
,
то говорят, что на множестве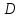 задана функция
задана функция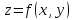 .
При этом переменные
.
При этом переменные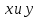 называются независимыми переменными,
а переменная
называются независимыми переменными,
а переменная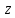 –зависимой
переменной
или функцией
двух переменных.
Множество
–зависимой
переменной
или функцией
двух переменных.
Множество
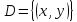 называется областью
определения
функции, а множество
называется областью
определения
функции, а множество
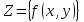 –множеством
значений
функции.
–множеством
значений
функции.
Геометрическим
изображением функции
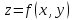 в прямоугольной системе координат
в прямоугольной системе координат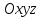 является некоторая поверхность.
является некоторая поверхность.
Линией
уровня
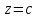 функции
функции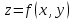 называется линия на плоскости
называется линия на плоскости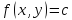 .
В каждой точке, лежащей на этой линии,
функция
.
В каждой точке, лежащей на этой линии,
функция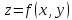 принимает значение, равное
принимает значение, равное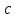 .
Поверхностью уровня
.
Поверхностью уровня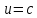 функции
функции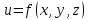 называется поверхность
называется поверхность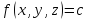 ,
в точках которой функция
,
в точках которой функция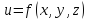 сохраняет значение, равное
сохраняет значение, равное .
.
Задания:
Найти области определения следующих функций:
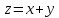 ;
б)
;
б)
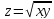 ;
в)
;
в)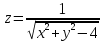 ;
г)
;
г)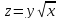
Построить линии уровней следующих функций (для
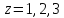 )
)
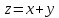 ;
b)
;
b)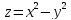 ;
c)
;
c)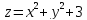
Частные производные. Производная по направлению. Градиент.
Определение
5.1. Частной
производной от функции
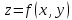 по независимой переменной
по независимой переменной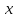 называется конечный предел
называется конечный предел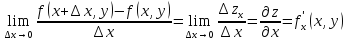 ,
вычисленный при постоянном значении
,
вычисленный при постоянном значении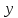 .
.
Для вычисления частных производных можно воспользоваться обычными правилами и формулами дифференцирования.
Пример
№16
Найти
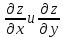 ,
если
,
если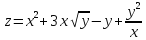
Решение:
При
вычислении
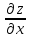 переменная
переменная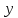 рассматривается как постоянная величина:
рассматривается как постоянная величина: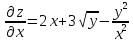 .
.
Рассмотрим
теперь переменную
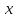 как постоянную величину:
как постоянную величину: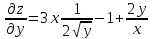 .
.
Задания:
Найти частные производные от функций:
a)
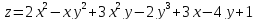 ;
;
b)
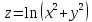 ;
;
c)
 ;
;
d)
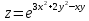 ;
;
e)
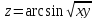 .
.
Показать, что данные функции удовлетворяют приведенным уравнениям:
а)
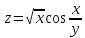 ;
;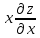 +
+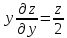 .
.
b)
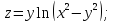
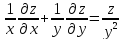 .
.
Определение
5.2.
Пусть
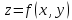 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки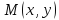 ,
пусть
,
пусть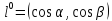 – единичный вектор, задающий направление
прямой
– единичный вектор, задающий направление
прямой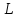 ,
проходящей через точку
,
проходящей через точку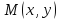 .
Выберем на прямой
.
Выберем на прямой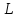 точку
точку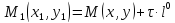 .
Рассмотрим приращение функции
.
Рассмотрим приращение функции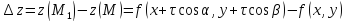 в точке
в точке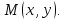 Предел отношения
Предел отношения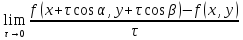 ,
если он существует, называетсяпроизводной
функции
,
если он существует, называетсяпроизводной
функции
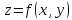 в точке
в точке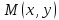 по направлению
по направлению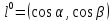 и обозначается
и обозначается
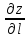 .
.
Если
функция
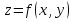 имеет в точке
имеет в точке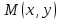 непрерывные частные производные, то в
этой точке существует и производная по
любому направлению, исходящему из точки
непрерывные частные производные, то в
этой точке существует и производная по
любому направлению, исходящему из точки ;
вычисляется эта производная по формуле
;
вычисляется эта производная по формуле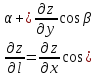 ,
где
,
где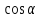 и
и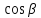 - направляющие косинусы вектора
- направляющие косинусы вектора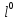 .
.
Пример №17
Вычислить
производную функции
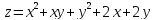 в точке
в точке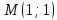 по направлению вектора
по направлению вектора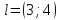 .
.
Решение:
Находим
единичный вектор
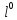 ,
совпадающий с направлением вектора
,
совпадающий с направлением вектора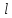 (т.е. найдем орт вектора
(т.е. найдем орт вектора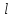 :
: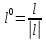 =
=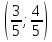 ,
т.е.
,
т.е.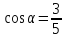 ,
,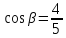 .
Находим частные производные
.
Находим частные производные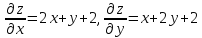 и вычисляем их значение в точке
и вычисляем их значение в точке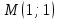 :
: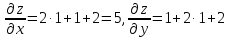 =5.
Тогда
=5.
Тогда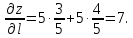
Определение
5.3.
Градиентом функции
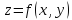 в точке
в точке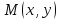 называется вектор с началом в точке
называется вектор с началом в точке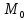 ,
координаты которого равны соответствующим
частным производным
,
координаты которого равны соответствующим
частным производным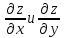 ,
вычисленным в точке
,
вычисленным в точке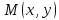 .
Градиент обозначается
.
Градиент обозначается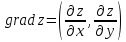 .
.
Аналогично
определяется производная по направлению
и градиент для функции трех переменных
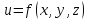 в точке
в точке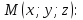
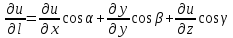 ;
;
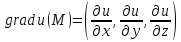 ,
где
,
где
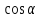 ,
,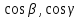 - направляющие косинусы вектора
- направляющие косинусы вектора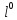
Пример
№18
Найти градиент функции
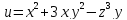 в точке
в точке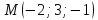 .
.
Решение:
Находим частные производные данной
функции:
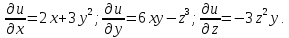
Вычисляем
значения этих производных в точке
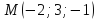 :
:
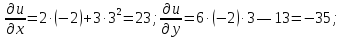
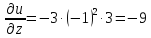 .
.
Окончательно
получаем
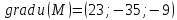 .
.
Задания:
Найти производные приведенных функций по направлению вектора
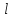 в заданной точке:
в заданной точке:
a)
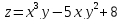 ,
,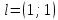 в
точке
в
точке ;
;
b)
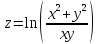 ,
,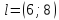 в
точке
в
точке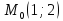 ;
;
c)
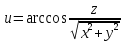 ,
,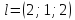 в
точке
в
точке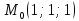 .
.
2. Найти градиент следующих функций:
а)
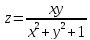 в точке
в точке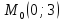 ;
;
b)
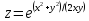 в точке
в точке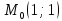 ;
;
c)
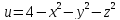 в точке
в точке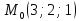 ;
;
d)
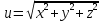 в точке
в точке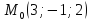 .
.
