Доведення деяких рівностей і тотожностей методом математичної індукції
Приклад №1
Довести методом математичної індукції, що для nєN
.
Доведення
1) Перевіримо, чи справджується ця формула при n=1:
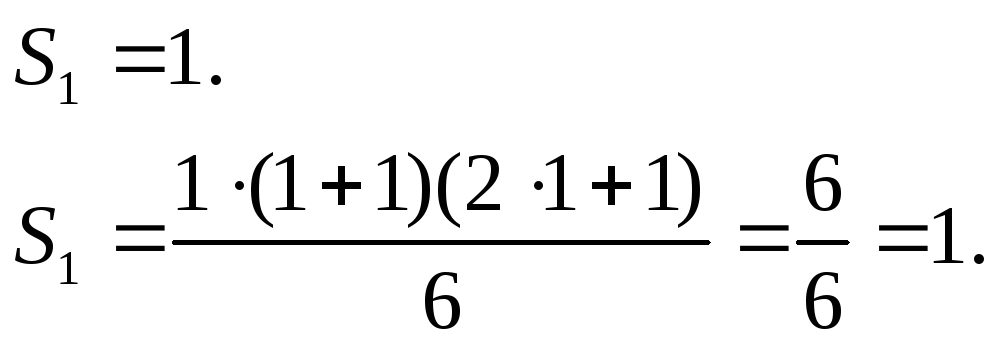
Так, формула справджується.
2) Припустимо, що формула справджується при n=k, тобто
(*)
Доведемо справедливість формули при n=k+1. Тобто покажемо, що
З іншого боку
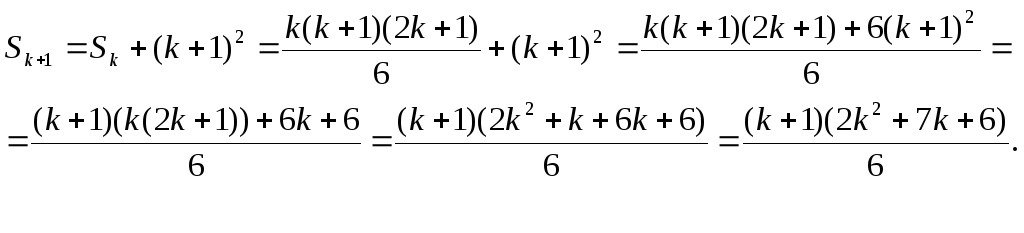
Розкладемо
на множники тричлен
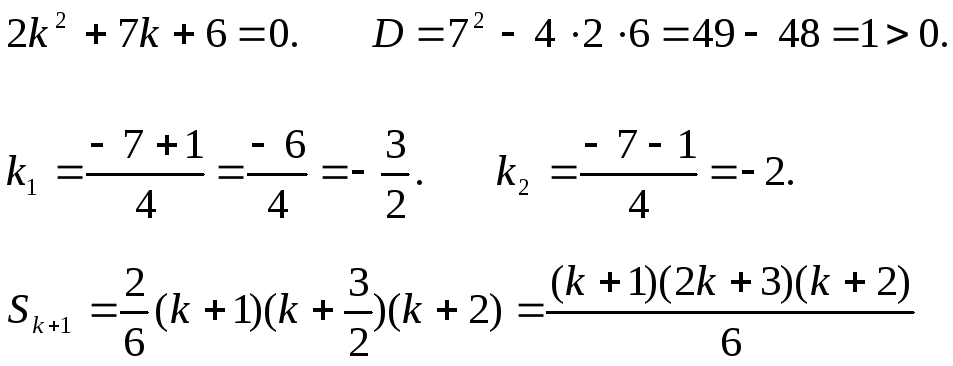
Отже, формула справджується при n=k+1. Тоді вона вірна і для будь-якого n натурального за принципом математичної індукції.
Приклад №2
Довести,
що виконується рівність
при будь-якому натуральному n.
Доведення
1) При n=1
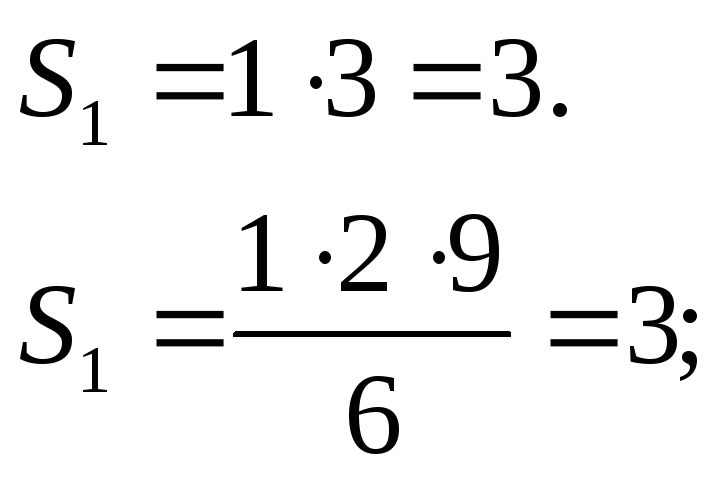
3=3 формула вірна.
2) Зробимо припущення, що дана формула справедлива і при n=k, тобто має місце рівність
Доведемо, що формула вірна і при n=k+1.
.
Враховуючи припущення, маємо
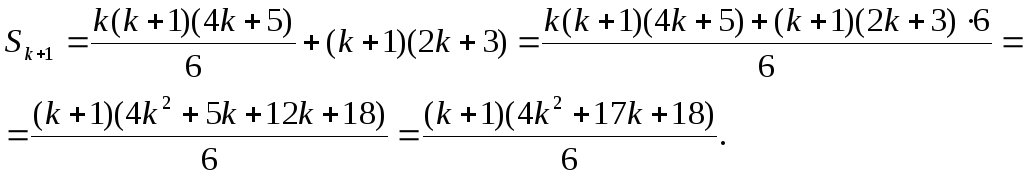
Розкладемо
на множники тричлен
:
Отже
Формула вірна і при n=k+1.
За
принципом математичної індукції вона
вірна і при
Висновок
Вчастности вивчивши метод математичної індукції, я підвищив знання у цій облас-ти математики, і навіть навчився виконувати завдання, які раніше мені у змозі.
У це були логічні ізанима-тельние завдання, тобто. саме ті, якіпови-шают інтерес до самої математиці як до науки. Рішення завдань стаєзаниматель-ним заняттям і може залучитиматематиче-ские лабіринти все нових допитливих. По-моєму, це є основою будь-який науки.
Продовжуючи вивчати метод математичної індукції, я постараюся навчитися застосовувати його не у математиці, а й у рішенні проблем фізики, хімії і найбільш життя.
Список літератури
Ш.Г.Горделадзе, М.М.Кухарчук, Ф.П.Яремчук “Збірник конкурсних задач з математики”. “Вища школа”, К., 1976, стор 201, 202, 173.
М.Б.Балк, Г.Д.Балк “Математика после уроков”. “Просвещение”,1971, стр 277, 282.
Р.Курант, Г.Роббинс “Что такое математика ?”. М., 1967 стр 34 – 44.
А.В.Шевченко “Математична індукція”. Київ, 1996.
Г.И.Глейзер “История математики в школе IX – X классы” стр 53.
В.А.Кречмар “Задачник по алгнбре”, М., 1968 стр. 92, 335.
В.Г.Болтянский, Ю.В.Сидоров, М.И.Шабунин, А.Г.Мордкович “Математика” Минск, 1996, стр 471.
