Метод математичної індукції в прикладах і задачах на обчислення сум, добутків

Приклад №1

Знайти формулу для обчислення суми S_n=.

Використаємо неповну індукцію. Розглянемо частинні випадки:

n=1 S₁=

n=2 S₂=

n=3 S₃=

n=4 S₄=

n=5 S₅=

Можна зробити припущення, тобто виказати гіпотезу, що S_n=.

Доведемо цю формулу методом математичної індукції.

Доведення

1) Базис індукції: При n=1 S₁==формула вірна.

2) Індуктивний перехід:

Припустимо, що дана рівність має місце при n=k, тобто S_k=.()

Виходячи із цього припущення. Доведемо, що воно істине і для n=k+1, тобто, що

S_k+1=, S_k+1= S_k+.

Враховуючи припущення () маємо: S_k+1==.

Отже, формула вірна і при n=k+1. За принципом математичної індукції вона справджується і при будь-якому n.

Приклад №2

Знайти формулу для обчислення суми S_n=.

Використаємо неповну індукцію. Розглянемо частинні випадки:

n=1 S₁=n=2 S₂=

n=3 S₃=n=4 S₄=

Можна зробити припущення, тобто виказати гіпотезу, що S_n=.

Доведемо цю формулу методом математичної індукції.

Доведення

1) Базис індукції: При n=1 S₁==формула вірна.

2) Індуктивний перехід:

Припустимо, що дана рівність має місце при n=k, тобто =.

Виходячи із цього припущення. Доведемо, що воно істине і для n=k+1, тобто, що

S_k+1=

Враховуючи припущення маємо: S_k+1==.

Отже формула вірна і при n=k+1. За принципом математичної індукції вона справджується і при будь-якому n.

Узагальнення методу математичної індукції

В деяких задачах трапляється, що твердження, яке необхідно довести, має місце не для всіх натуральних значень n, а лише для значень n, починаючи з певного натурального числа n_о. У таких випадках можна скористатися узагальненим принципом математичної індукції.

Сформулюємо цей принцип:

Нехай твердження, що залежить від натурального числа n, задовольняє такі умови:

1. Це твердження є правильним при n=n_о;

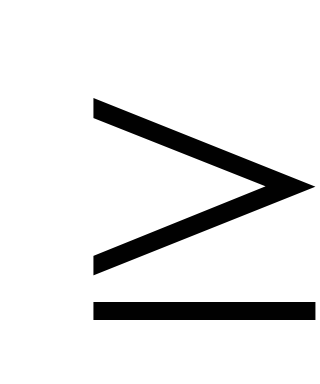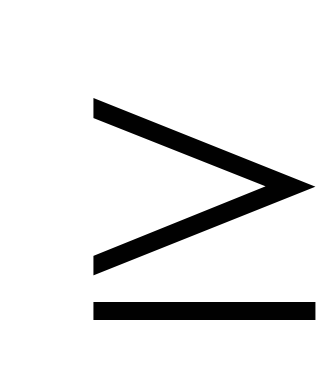2. З припущення правильності даного твердження при n=k (де kn_о) випливає його істинність і при n=k+1. Тоді дане твердження справджується при всіх натуральних nn_о.

Необхідно розуміти, що при значеннях n<n_о твердження може бути як вірним так і невірним; у всякому разі, яких-небудь заключень щодо істинності твердження при 1n < n_o з проведеного доведення методом математичної індукції зробити не можна.

Наведемо приклади використання узагальненого принципу математичної індукції.

Розглянемо одну з геометричних задач на доведення.

Приклад №1

Теорема.

Кількість діагоналей опуклого n – кутника дорівнює . Довести це.

Доведення.

Нехай . Найменша кількість сторін n-кутника n=3 у трикутника.

при n=3 D(3)==0. Це вірно, тому що у трикутника діагоналей немає. Отже при n=3 вихідне твердження істинне.

Припустимо, що у будь-якому опуклому k-кутнику кількість діагоналей D(k)=(n=k).

Враховуючи дане припущення, доведемо, що у опуклому (k+1)-кутнику кількість діагоналей .

Нехай А₁А₂А₃…А_KA_K+1 – опуклий (k+1)-кутник. Проведемо в ньому діагональ A₁A_K. Щоб порахувати спільну кількість діагоналей цього (k+1)-кутника, необхіднодо кількості діагоналей k-кутника, тобто, враховуючи припущення, до числа додати 1 ( це діагональ А₁А_K ) і число (k-2) – кількість діагоналей (k+1)-кутника, які виходять з вершини А_k+1.

Таким чином,

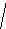
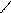
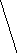
D(k+1)=D(k)+(k-2)+1=

.

Отже, твердження справджується і при n=k+1. За принципом математичної індукції воно істинне і для будь-якого опуклого n-кутника.

P.S. Цю теорему можна довести і по-іншому, з використанням відомої формули комбінаторики. , де,.

Доведення.

Кожна пара вершин цього n-кутника визначає або сторону, або діагональ. Отже, всього маємо , що й треба було довести.

Узагальнений принцип інколи використовують і при доведенні нерівностей.