Глава 2 анализ и синтез логических схем

2.1. Потенциальные и импульсные сигналы

Сигнал называется потенциальным, если интервал времени между соседними изменениями сигнала значительно больше времени реакции схемы, в которой он используется. Если длительность активного уровня сигнала того же порядка, что и время реакции схемы, то сигнал называют импульсным.

x t

T1 T2 T3 T4 T5

dx

t

d

t

x

t

Рис. 2.1

При аналитическом описании схем используется понятие абстрактного импульсного сигнала, длительность которого бесконечно мала, в отличие от реального импульсного сигнала, имеющего конечную длительность. Понятие абстрактного импульсного сигнала позволяет абстрагироваться от параметров конкретных схем. Импульсные сигналы порождаются изменениями потенциальных сигналов с 1 на 0 и наоборот.

Для описания изменений потенциальных сигналов и порождаемых ими импульсных сигналов удобно использовать математический аппарат, основанный на операторах перехода d, и . Импульсные сигналы dx, и x показаны на рис. 2.1.

Оператор переходов d определяется соотношением

(2.1)

где импульсный сигнал, порождаемый изменениями потенциального сигнала с 0 на 1;- значение потенциального сигнала в данный момент времени;- значение потенциального в предыдущий момент времени.

Очевидно, что только при изменении потенциального сигнала с 1 на 0.Абстрактный потенциальный сигнал имеет бесконечно крутые фронты, поэтому для абстрактного импульсного сигнала в соотношении (2.1) Введя для сигналов обозначенияполучим:

(2.2)

Соотношение (2.2) учитывает время в явной форме и может использоваться не только для потенциальных сигналов, но и для переключательных функций от потенциальных сигналов:

(2.3)

где- значения функции в данный момент времени,- значение функции в предыдущий момент времени. Из соотношения (2.3) следует, что импульсные сигналы, порождаемые переключательными функциями могут быть получены с помощью основных операций алгебры логики. Так, еслито

(2.4)

где только при изменении потенциального сигнала с 0 на 1.

Имеет тождество которое отражает тот факт, что потенциальный сигнал не может изменяться одновременно с 0 на 1 и с 1 на 0. Следует помнить, что сигналыс точки зрения алгебры логики являются переменными, но поскольку их значения совпадают со значениями одного и того же сигнала в различные моменты времени, то операторные соотношения учитывают время в явном виде.

Оператор переходов  определяется соотношением

(2.5.)

где при изменении потенциального сигналаx как с 0 на 1, так и с1 на 0.

Легко доказать основные операторные тождества:

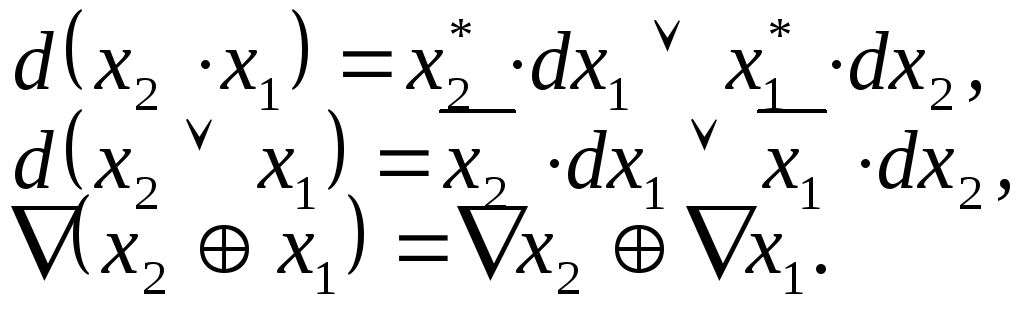
 (2.6)

Докажем первое тождество:

Тождества (2.6) поясняются временными диаграммами, изображенными на рис. 2.2.

x₂

t

x₁

t

x₂x₁

t

d(x₂x₁)

t

x₂+x₁

t

d(x₂+x₁)

t

x₂x₁ t

(x₂x₁)

t

Рис. 2.2

Как известно, для обычных тождеств алгебры логики справедлив принцип двойственности, устанавливающий правило, на основании которого для любого тождества можно получить двойственное ему тождество. Это утверждение справедливо и для операторных тождеств, что позволяет разбить их на пары: