
Задание №9.
Разложить рациональную функцию на простейшие дроби (коэффициенты не вычислять)
9.1
![]() ;
;
9.2
![]() ;
;
9.3
![]() ;
;
9.4
![]() ;
;
9.5
![]() ;
;
9.6
![]() ;
;
9.7
![]() ;
;
9.8
![]() ;
;
9.9
![]() ;
;
9.10
![]() ;
;
9.11
![]() ;
;
9.12
![]() ;
;
9.13.
![]() ;
;
9.14.
![]() ;
;
9.15
![]() ;
;
9.16
![]() ;
;
9.17
![]() ;
;
9.18
![]() ;
;
9.19
![]() ;
;
9.20
![]() ;
;
9.21
![]() ;
;
9.22
![]() ;
;
9.23
![]() ;
;
9.24
![]() ;
;
9.25
![]() ;
;
9.26
![]() ;
;
9.27![]() ;
;
9.28
![]() ;
;
9.29
![]() ;
;
9.30
![]() ;
;
Задание №10
Найти неопределенные интегралы. Результаты двух каких-нибудь интегрирований проверить дифференцированием. Под б) и в) найти интегралы двумя способами.
а)
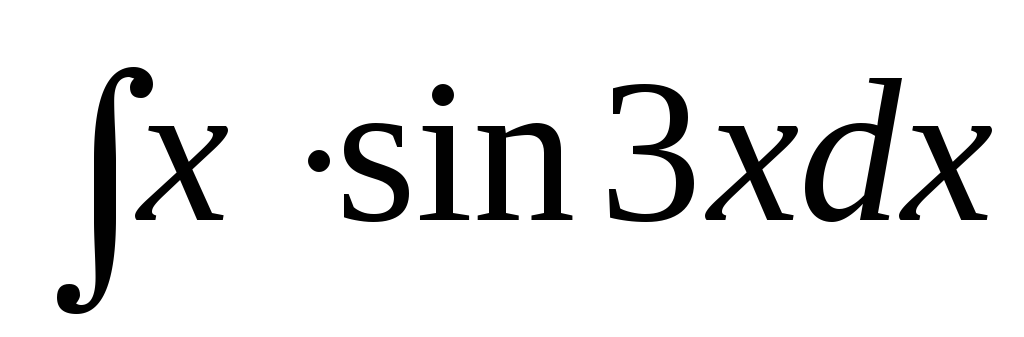 ; б)
; б) ; в)
; в) ;
;
г)![]() ;
д)
;
д)![]() .
.
а)
 ; б)
; б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ; в)
; в)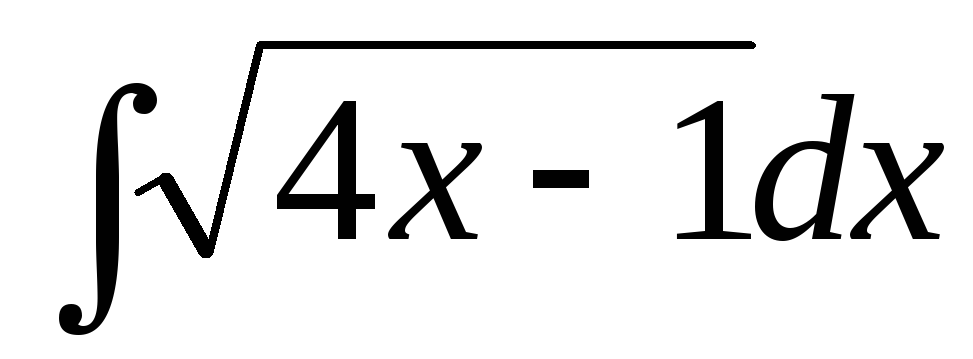 ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ;
в)
;
в)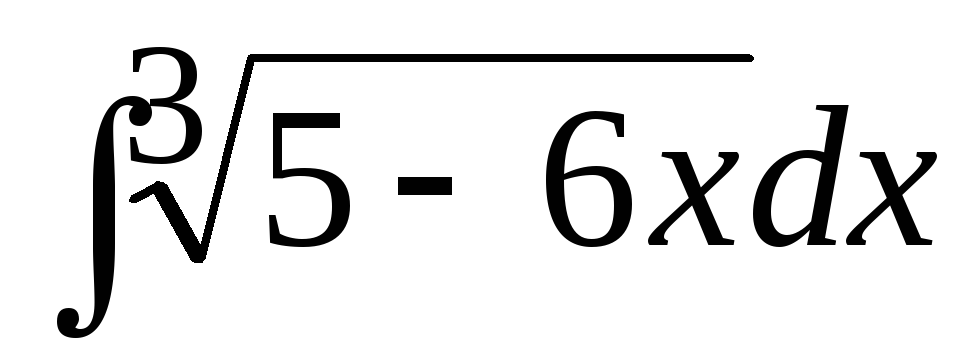 ;
;
г)![]() ;
д)
;
д)![]() .
.
а)
 ; б)
; б) ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б)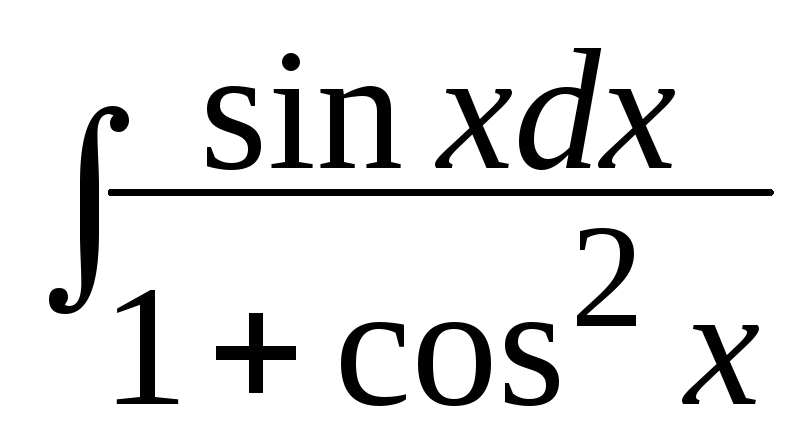 ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
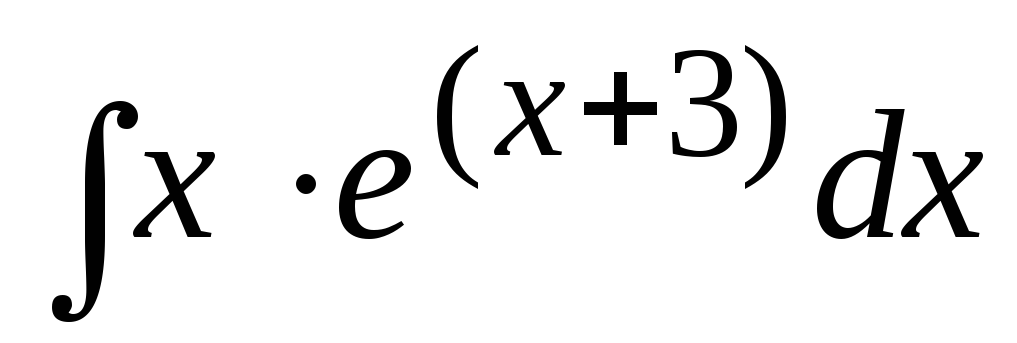 ; б)
; б)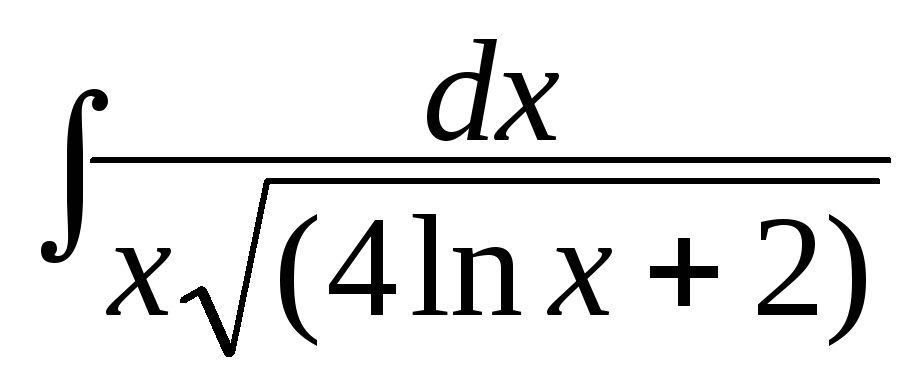 ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ; в)
; в) ;
;
г)![]() ; д)
; д)![]()
а)
 ; б)
; б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б)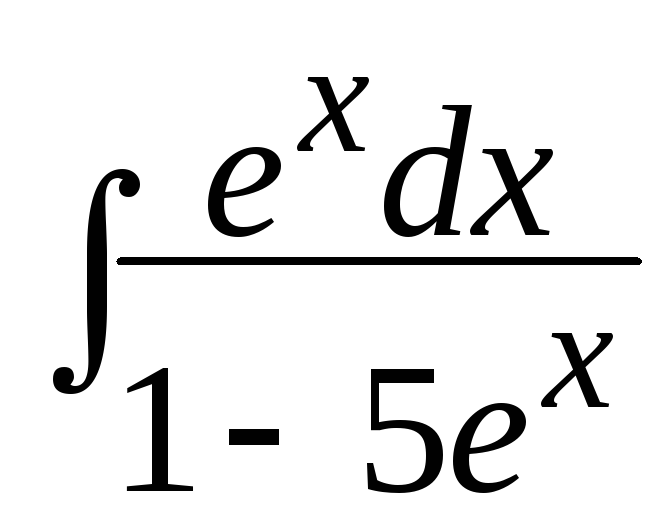 ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в)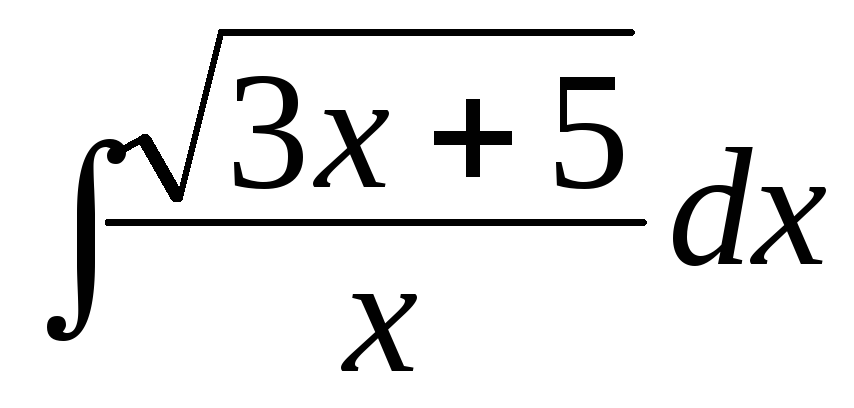 ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ; в)
; в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ; б)
; б) ; в)
; в)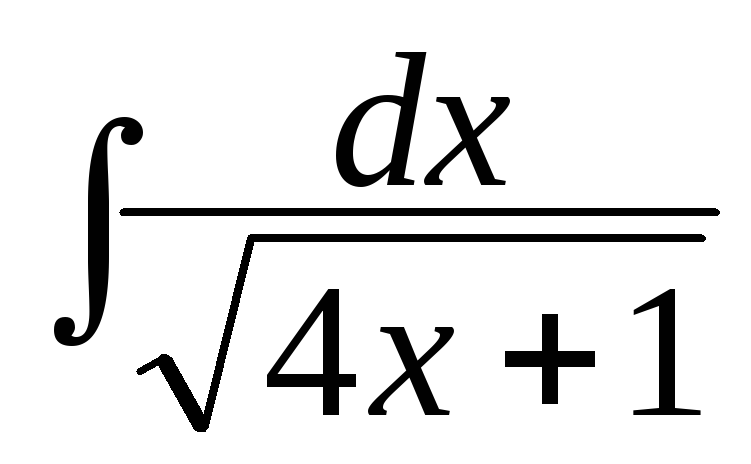 ;
;
г)![]() ; д)
; д)![]() .
.
а)
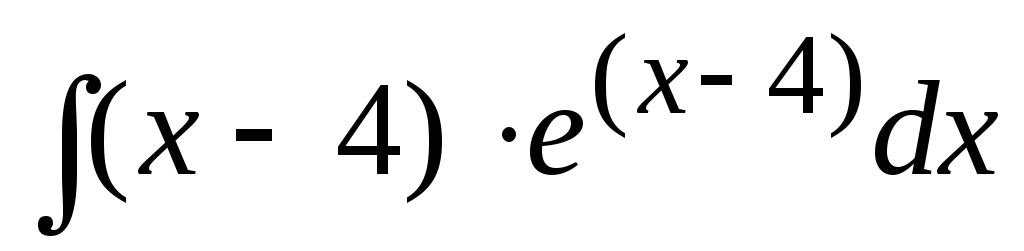 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
а)
 ;
б)
;
б) ;
в)
;
в) ;
;
г)![]() ; д)
; д)![]() .
.
Задание №11.
Вычислить площадь фигуры, ограниченной указанными линиями
11.1.![]() ,у
= 0, х
= 1, х
= е
11.2.
,у
= 0, х
= 1, х
= е
11.2.![]() ,х
= 0, y
= 0, x
= 2
,х
= 0, y
= 0, x
= 2![]() .
.
11.3. y
= x![]() ,
y
= 8, x
= 0. 11.4.
y
= ex,
y
= e–x,
x
= 1.
,
y
= 8, x
= 0. 11.4.
y
= ex,
y
= e–x,
x
= 1.
11.5. x
= tg x,
x
=
![]() ,x
= –
,x
= –
![]() ,y
= 0.
,y
= 0.![]() 11.6. xy
= 6, y
= 7 – x.
11.6. xy
= 6, y
= 7 – x.
11.7. y
=
![]() +
+![]() ,x
+ y=
2, x
= 2. 11.8. y
= 4 –
,x
+ y=
2, x
= 2. 11.8. y
= 4 –![]() ,
y
=
,
y
=
![]() –
2x.
–
2x.
11.9. y
= arccos x,
x
= 0, y
= 0. 11.10. y
=
![]() ,y
= 0, x
= 1.
,y
= 0, x
= 1.
11.11. y
=
![]() ,
y
=
,
y
=
![]() ,y
= 3x.
11.12. y
= 6x
–
,y
= 3x.
11.12. y
= 6x
–![]() ,y
= 0.
,y
= 0.
11.13.
![]() ,y
= 0, x
=
,y
= 0, x
=
![]() .
11.14.y
= 2x
+ 1, x
– y
– 1 = 0.
.
11.14.y
= 2x
+ 1, x
– y
– 1 = 0.
11.15. y
=![]() y
=
y
=![]() .
11.16.
.
11.16.![]() + 8x
= 16,
+ 8x
= 16,
![]() –
24x
= 48.
–
24x
= 48.
11.17. y
=![]() ,y
=
,y
=![]() . 11.18.
. 11.18.![]() +
+![]() =
8,y
=
=
8,y
=
![]() .
.
11.19.
![]() =
6x,
=
6x,
![]()
![]() +
+
![]() =
13. 11.20. y
=
=
13. 11.20. y
=![]() ,y
=
,y
=
![]() .
.
11.21. y
= x
(x
–![]() ),
y
= 0. 11.22. y
= x
–
),
y
= 0. 11.22. y
= x
–![]()
![]() ,
y
= 0.
,
y
= 0.
11.23. y
= ln x
,
![]() x.
11.24. y
= sin x
, y
= cos x,
x
= –
x.
11.24. y
= sin x
, y
= cos x,
x
= –![]() ,x
=
,x
=
![]() .
.
11.25. y
= 0, y
= arcsin x,
y
= arccos x.
11.26. y
= (![]() +
2x)
+
2x)![]() ,y
= 0.
,y
= 0.
11.27. x
=
![]() (t
– sin t),
y
=
(t
– sin t),
y
=
![]() (1
–cost),
y
= 0. 11.28. x
=
(1
–cost),
y
= 0. 11.28. x
=
![]()
![]() t,
y
=
t,
y
=
![]()
![]() t.
t.
11.29. x
= 3![]() ,y
= 3t
–
,y
= 3t
–![]() ,петля.
11.30. x
=
,петля.
11.30. x
=
![]() –
1,y
=
–
1,y
=
![]() –t,
петля.
–t,
петля.
Задание №12.
Исследовать сходимость несобственного интеграла 1-ого рода.
12.1.![]() . 12.2.
. 12.2.
![]() . 12.3.
. 12.3.
![]() .
.
12.4.
![]() . 12.5.
. 12.5.![]() . 12.6.
. 12.6.![]() .
.
12.7.
![]() . 12.8.
. 12.8.![]() . 12.9.
. 12.9.![]() .
.
12.10.
![]() . 12.11.
. 12.11.![]() . 12.12.
. 12.12.![]() .
.
12.13.
![]() . 12.14.
. 12.14.![]() . 12.15.
. 12.15.![]() .
.
12.16.
![]() . 12.17.
. 12.17.![]() . 12.18.
. 12.18.![]() .
.
12.19.![]() . 12.20.
. 12.20.![]() . 12.21.
. 12.21.![]() .
.
12.22.
![]() . 12.23.
. 12.23.![]() . 12.24.
. 12.24.
![]() .
.
12.25.
![]() . 12.26.
. 12.26.![]() . 12.27.
. 12.27.![]() .
.
12.28.
![]() . 12.29.
. 12.29.![]() . 12.30.
. 12.30.![]() .
.
Задания типового расчёта №2
Темы:
«Обыкновенные дифференциальные уравнения»
«Функции нескольких переменных»
