14. 7. 2. Теплоемкость и степени свободы.

Равнораспределение энергии по степеням свободы. Из уравнения состоя­ния и основного уравнения молекулярно-кинетической теории

,

(14.22)

следует, что среднее значение кинетической энергии поступательного движения молекул

.

(14.23)

Заметим, что при построении модели идеальный газ представляли как систему, состоящую из абсолютно твердых молекул-шариков, взаимодействием между которыми мы пренебрегали. В этой модели молекула-шарик может двигаться в любом из трех пространственных направлений в однородном изотропном пространстве. Здравый смысл подсказывает, что ни одно из этих направлений не имеет преимущества перед двумя другими. Поэтому нетрудно сообразить, что в среднемдвижению в каждом из этих направлений соответствует энергия, пропорциональная, что в сумме дает.

Рассмотрим теперь молекулу, обладающую более сложной структурой.

Предположим, что молекула состоит из двух жестко связанных между собой атомов (рис. 14.5). Центр масс такой молекулы, совершающей поступательное движение, может перемещаться в пространстве в 3-х независимых направлениях, задаваемых осями (рис. 14.5а).

а)	б)
Рисунок 14. 5.

В системе отсчета, начало которой связано с центром масс молекулы, пространственное положение оси молекулы полностью определяется двумя углами: и(рис. 14.5б).

Молекула может произвольно вращаться вокруг своего центра масс. При этом она приобретает дополнительную кинетическую энергию, связанную с вращательным движением, величина которой определяется совокупностью двух членов:

и .

(14.24)

где и- составляющие угловой скорости вращения молекулы.

В теоретической физике доказывается, что в среднем составляющие кинетической энергии

.

(14.25)

Полная энергия такой молекулы

.

(14.26)

Назовем числом степеней свободы число независимых координат, которые следует задать для определения положения молекулы в пространстве.

Для одноатомной и многоатомных молекул всегда ; для рассматриваемой молекулы добавляются еще вращательные степени свободы:.

Т.о., и средняя кинетическая энергия молекулы газа

.

(14.27)

Рассмотрим двухатомную молекулу (рис. 14.6), связь между атомами которой упругая (в предыдущем случае связь меду молекулами предпола-

	галась жесткой). Тогда наряду с 5-тью степенями свободы, определяющими кинетическую энергию двухатомной молекулы с жесткой недеформи­руемой связью, при наличии упругой связи следует задать ещё одну.
Рисунок 14. 6.

Однако колебательное движение характеризуется наряду с кинетической еще и потенциальной энергией. Это означает, что при подсчете степеней свободы двухатомной молекулы с упругой связью между атомами мы должны записать

.

(14.28)

Из теории колебаний известно, что для гармонического осциллятора средние значения кинетической и потенциальной энергии одинаковы. Поэтому, по-прежнему, считая, что на каждую степень свободы молекулы приходится энергия, равная , получаем

.

(14.29)

И, наконец, если молекула является многоатомной и имеет сложную пространственную конфигурацию, то для её описания следует ввести еще одну вращательную степень свободы, т.е. число вращательных степеней свободы становится равным трем: .

В общем случае число степеней свободы молекулы определяется выражением ():

,

где ,и, а среднее значение энергии молекулы в соответствии с принципом равнораспределения по степеням свободы равно

.

(14.30)

Это уравнение (14.30) выражает закон классической статистической физики, утверждающий, что на каждую степень свободы системы, находящейся в состоянии термодинамического равновесия, приходится в среднем энергия, равная (закон равнораспределения энергии по степеням свободы).
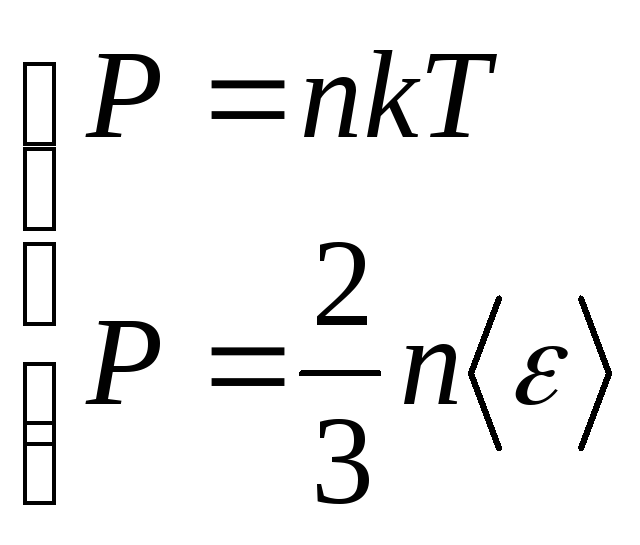