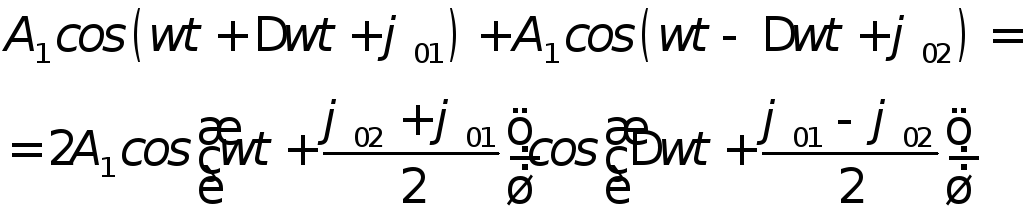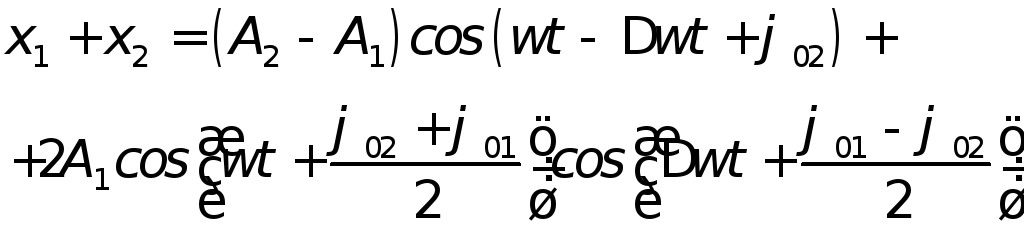- •Лекция 10.
- •9. 1. Сложение гармонических колебаний.
- •9.1. Сложение колебаний одного направления одинаковой частоты.
- •9. 1. 1. Сложение колебаний одного направления с близкими частотами. Биения.
- •9. 2. Сложение перпендикулярных колебаний.
- •9. 2. 1. Сложение перпендикулярных колебаний одинаковой частоты.
- •9. 2. 2. Сложение перпендикулярных колебаний кратных частот. Фигуры Лиссажу.
- •9. 3. Понятие о разложении колебаний в ряд Фурье.
- •9. 4. Затухающие колебания.
- •9. 4. 1 Добротность.
Федун В.И. Конспект лекций по физике Механические колебания и волны
Лекция 10.
9. 1. Сложение гармонических колебаний.
9.1. Сложение колебаний одного направления одинаковой частоты.
Наиболее простым примером является сложение двух одинаково направленных гармонических колебаний одинаковой частоты, каждое из которые можно представить в аналитическом виде
|
|
(9.1) |
|
и
|
(9.2) |
В векторном виде эти колебания представлены на рисунке 9.1.
|
A2 2-1 02 2 A1 011
x1 x2
|
Поскольку
оба слагаемых вектора вращаются с
одинаковой частотой, то суммарный
вектор также будет вращаться с этой
же частотой. Следовательно, результатом
суммы
| |
|
Рисунок 9. 1. | ||
|
|
(9.3) | |
Определим разность
начальных фаз
![]() из рисунка 9.1. Выразим тангенс начальной
фазы
из рисунка 9.1. Выразим тангенс начальной
фазы![]() результирующего колебания так:
результирующего колебания так:
|
|
(9.4) |
где
![]() и
и![]() -проекции амплитуды суммарного колебания
на оси
-проекции амплитуды суммарного колебания
на оси![]() и
и![]() ,
соответственно. Как следует из рисунка
5, значение
,
соответственно. Как следует из рисунка
5, значение![]() равно сумме проекций на ось
равно сумме проекций на ось![]() каждого из слагаемых колебаний:
каждого из слагаемых колебаний:
|
|
(9.5) |
Аналогичное
получаем выражение для суммарной
проекции на ось
![]()
|
|
(9.6) |
Тогда
|
|
(9.7) |
Таким образом, определены основные параметры суммарного колебания: амплитуда, частота и начальная фаза.
9. 1. 1. Сложение колебаний одного направления с близкими частотами. Биения.
Несколько сложнее найти сумму двух колебаний одного направления, если их частоты отличаются друг от друга. Практически интересным является случай, когда это различие незначительно, т.е.
|
|
и |
|
причем
![]() .
Получим аналитически результат такого
сложения.
.
Получим аналитически результат такого
сложения.
Биения.
Сначала рассмотрим достаточно простой
случай токого сложения, когда амплитуды
таких колебаний равны (![]() =
=![]() ).
Тогда имеем колебания
).
Тогда имеем колебания
|
|
(9.8) |
и
|
|
(9.9) |
Поскольку
![]() ,
то
,
то
|
|
(9.10) |
Здесь величину
![]() можно рассматривать как медленно
меняющуюся амплитуду. Пусть для простоты
начальные
можно рассматривать как медленно
меняющуюся амплитуду. Пусть для простоты
начальные
|
|
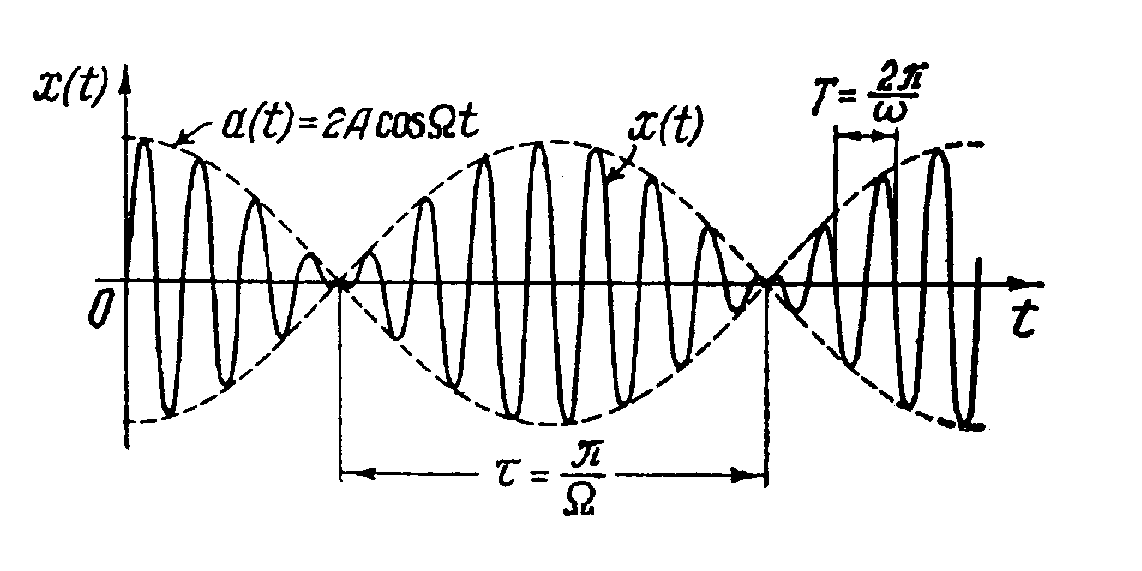
фазы обоих колебаний одинаковы. Результат суммы таких колебаний, представленный на рис. 9.2, называется биениями. Примером биений является известное «завывание» двигателей многомоторных самолетов. |
|
Рисунок 9. 2. |
Теперь рассмотрим более сложный случай, когда амплитуды слагаемых колебаний неодинаковы.
Пусть амплитуда
второго
![]() колебания больше амплитуды
колебания больше амплитуды![]() первого колебания. Тогда имеем колебания
первого колебания. Тогда имеем колебания
|
|
(9.11) |
и
|
|
(9.12) |
Поскольку
![]() ,
то
,
то
|
|
|
и
|
|
(9.13) |
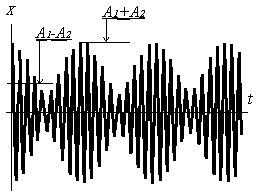
Получили достаточно сложное для восприятия аналитическое выражение. Результат приобретает более наглядный вид при построении графика такого сложения колебаний (см. рис. 9.3).
|
|
Картина
наблюдающихся биений отличается от
предыдущей, т.к. теперь суммарная
амплитуда изменяется от значения
|
|
Рисунок 9. 3. |