Лекции теплотехника часть 2

1 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1 Общие положения

Основной задачей расчета нагрева или охлаждения тел (процесса нестационарной теплопроводности) является нахождение изменения температур во времени по сечению тела. При нагреве* по сечению тела возникает перепад температур. В некоторых случаях разность температур по сечению получается таковой, что в данных условиях нагрева ей можно пренебречь. Такие тела называют термически “тонкими”. Если же пренебречь перепадом температур по сечению нельзя, то такие тела называют термически “массивными”.

Тепловая “массивность” тела определяется его размерами, теплофизическими свойствами и скоростью нагрева. Для установления границ “тонких” и “массивных” тел пользуются критерием (числом)

Био

где – коэффициент теплоотдачи от окружающей среды к поверхности тела при его нагреве, или от поверхности тела к окружающей среде при его охлаждении, Вт/(м2·К);

S – толщина прогрева (характерный размер), м;

– коэффициент теплопроводности тела, Вт/(м·К). Толщина прогрева определяется по формуле:

где – коэффициент несимметричности;

δ – размер тела в направлении действия теплового потока (например, для бесконечной пластины - ее толщина, для цилиндра бесконечной длины и шара - диаметр), м.

Значение коэффициента несимметричности зависит от условий подвода теплоты к поверхностям тел и может быть рассчитано по следующей формуле:

где q1 и q2 – тепловые потоки на противоположных поверхностях нагреваемого изделия.

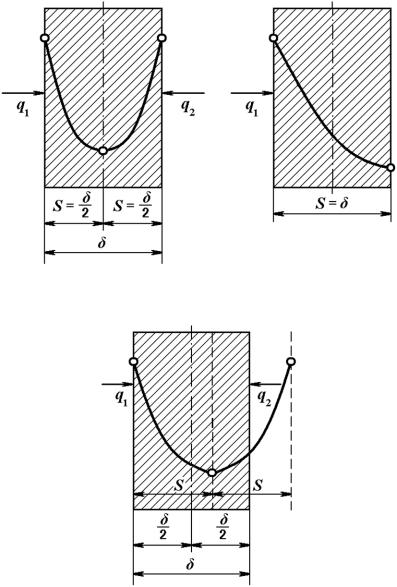
Так, например, при симметричном нагреве пластины (т.е. к обеим

* далее речь будет вестись о нагреве тел, но при этом все формулы справедливы и для процессов охлаждения

ее поверхностям подводятся одинаковые тепловые потоки: q1 = q2) распределение температуры по ее сечению будет параболическим, причем вершина параболы совпадает с геометрической осью пластины (рис. 1.1. а), следовательно, в этом случае = 0,5. При односто-

роннем нагреве тепловой поток подводится только к одной поверхности пластины, значит q2 = 0, а = 1 (рис. 1.1, б). При несимметричном

нагреве q1 ≠ q2, поэтому вершина параболы, изображающей распределение температур по сечению пластины, будет смещена относительно ее геометрической оси (рис. 1.1, в), а коэффициент несимметричности 0,5 < < 1.

Если рассчитанное по (1.1) значение критерия Bi < 0,25, тело считается термически “тонким”, при Bi > 0,5 – термически “массивным”. В пределах 0,25 < Bi < 0,5 находится переходная область. При расчете нагрева тел, попадающих в эту область, целесообразно рассматривать их как термически “массивные”.

В случае лучистого теплообмена тепловая “массивность” тел определяется по значению критерия Старка

где пр – приведенный коэффициент излучения, Вт/(м2·К4);

То.с. – температура окружающей среды, К.

Если значение Sk < 0,15, тело считается термически “тонким”.

Втех случаях, когда нагрев происходит одновременно конвекцией

иизлучением область “тонких” тел определяют из выражения:

При нагреве “массивных” тел в печах при условии адиабатности кладки в качестве параметра интенсивности внешнего теплообмена можно пользоваться понятием условного коэффициента теплоотдачи излучением, который определяется по формуле:

где Tпеч ( tпеч ) – температура печи, К (°С);

Tп ( tп ) – температура поверхности нагреваемого изделия, К (°С).

в)

Рис. 1.1 Распределение температуры по сечению пластины при различных условиях ее нагрева

1.2 Расчет нагрева термически “тонких” тел 1.2.1 Конвективный теплообмен при постоянной температуре

окружающей среды (граничные условия III рода)

Перепадом температуры по сечению “тонкого” тела пренебрегают, следовательно, отпадает необходимость рассматривать и решать задачу о распространении тепла внутри этого тела. Тогда вопрос об определении времени нагрева сводится к решению простого уравнения, показывающего, что все подведенное к поверхности нагреваемого “тонкого” тела тепло расходуется на изменение его энтальпии.

Количество тепла dQ, получаемое телом с тепловоспринимающей поверхностью F от среды с постоянной температурой tо.с. за время dτ в результате конвективной теплоотдачи к поверхности нагреваемого тела равно:

где c – удельная теплоемкость тела, Дж/(кг·К); M – масса тела, кг;

dt – изменение температуры тела.

Приравняв правые части равенств (1.7) и (1.8), разделив переменные и проинтегрировав от начального момента времени (τ = 0), когда температура тела равна tн, до момента времени τ, когда температура тела равна tк, получим:

tо.с. t Fd cMdt ;

Решение обратной задачи, т.е. значение температуры тела в момент времени τ, будет иметь вид:

Для тел простой формы (бесконечная пластина, цилиндр бесконечной длины*, шар) выражения (1.9) и (1.10) можно представить в виде:

где ρ – плотность тела, кг/м3;

k – коэффициент формы (для пластины k = 1, для цилиндра k = 2, для шара k = 3).

1.2.2 Теплообмен излучением при постоянной температуре окружающей среды (граничные условия III рода)

Рассуждаем аналогично п.1.2.1.

Количество тепла dQ, получаемое телом от среды с постоянной температурой Tо.с. за время dτ в результате теплообмена излучением равно:

следовательно, уравнение теплового баланса в данном случае будет иметь вид:

Разделяя переменные и интегрируя, найдем время нагрева тела τ от начальной Тн до конечной Тк температуры:

* если длина и ширина прямоугольной заготовки много больше толщины, то при расчетах ее можно считать бесконечной пластиной, аналогично, если длина цилиндрической заготовки много больше диаметра, то в расчетах ее принимают как цилиндр бесконечной длины

В полученной выше формуле члены в круглых скобках представляют собой одинаковые функции отношения температур, поэтому ее можно записать в следующем виде:

Для тел, имеющих форму пластины, цилиндра и шара выражение (1.16) можно представить в виде:

1.3 Расчет нагрева термически “массивных” тел 1.3.1 Дифференциальное уравнение теплопроводности

Дифференциальное уравнение теплопроводности, в основу вывода которого положены закон сохранения энергии и закон Фурье, выражает связь между изменением температуры во времени и ее распределением в пространстве. В декартовой системе координат при отсутствии внутренних источников теплоты дифференциальное уравнение теплопроводности имеет вид:

где a – коэффициент температуропроводности, м2/с.

Коэффициент температуропроводности является физическим параметром вещества. Он характеризует скорость изменения температуры и определяется соотношением:

где – коэффициент теплопроводности тела, Вт/(м·К); c – удельная теплоемкость тела, Дж/(кг·К);

– плотность тела, кг/м3.

Дифференциальное уравнение теплопроводности в цилиндрической системе координат r-φ-z при отсутствии внутренних источников теплоты таково:

где r – радиус-вектор; φ – полярный угол;

z – аппликата.

Задавая условия однозначности и интегрируя дифференциальное уравнение, можно получить распределение температуры в теле и ее изменение во времени для конкретного случая. Однако необходимо отметить, что аналитическое решение уравнений (1.18) и (1.20) возможно лишь для тел простой формы (бесконечная пластина, цилиндр бесконечной длины), но даже в этом случае формулы получаются весьма сложными, поэтому при технических расчетах процессов нагрева обычно пользуются специальными графиками и номограммами.