Лекція 12 Стійкість стиснутих стержнів

План лекції:

1. Типи конструкційної стійкості стержнів

2. Формула Ейлера для визначення критичної сили

3. Поняття про критичні напруження. Емпіричні залежності Ясинського

4. Основні типи розрахунків стержнів на стійкість

Література : [1] - ст. 491 - 508. [2] - ст. 619 - 644.

Стійка конструкція - це конструкція, яка зберігає під дією зовнішнього навантаження свою початкову форму пружної рівноваги.

Р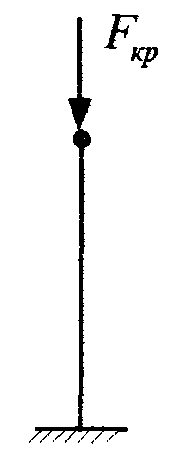озглянемо випадокстискання стержня поздовжнім зусиллям.

Існує три стани тіла в одному із яких воно може при цьому перебувати: - стійка рівновага – це коли при незначному відхиленні від стану рівноваги тіло намагається повернутися в своє початкове положення; – нестійка рівновага – коли тіло виведене з положення рівноваги зовнішнім зусиллям продовжує деформуватись в напрямку його дії, і в своє початкове положення не повертається; – байдужа, або критична рівновага – тіло при цьому стані знаходиться в початковій своїй формі, але навіть при незначному зростанні діючого зовнішнього зусилля може її втратити.

Сила, що відповідає даному стану називається критичною, позначається ().

Критичною – називається сила, найменше перевищення якої приводить до втрати стійкого положення рівноваги тіла, чи конструкції.

(1)

де – допустиме навантаження при розрахунку на стійкість.

–коефіцієнт запасу стійкості.

Для забезпечення запасу стійкості необхідно, щоб виконувалась основна умова:

(2)

чи так:

Зруйнування конструкції від втрати стійкості є одним із небезпечних видів руйнувань, адже відбувається при напруженнях значно менших за.

, (3)

де.

–для пластичних матеріалів;

–для анізотропних матеріалів (дерево і йому подібні);

–для крихких матеріалів (чавун, скло).

Формула Ейлера для визначення при визначенні стійкості

стиснутих стержнів.

Для визначення Ейлер домагався незначних відхилень стержня від його початкового положення, при цьому (пропорційності)-

Через те, що деформації при цьому були дуже малі, використовувалось ДР пружної лінії для балки:

, (4)

при цьому, для розрахунку приймається, що (ЕІ) мінімальна.

В правій частині ДР (4) завжди буде знак "–" оскільки знак прогину і знак другої похідної від нього, тобто моменту, що визвав цей прогин, будуть різні, при любому ().

При і навпаки,

, (6)

де. Перепишемо (6) так:

Позначимо:. Тоді:

(7)

Розв'язком цього рівняння буде вираз:

,

1. При:.

2. При:, а так як, то.

Відповідно:. Тоді:(8)

Ця формула вперше була отримана для шарнірно закріпленого стержня. При визначенні максимального прогину необхідно взяти першу похідну по від -,тобто визначити екстремум функції прогину.

Оскільки, то, то(9)

При тобто посередині стержня, от же – це число напівхвиль, що можуть бути розміщені по довжині стержня.

Поняття про приведену довжину стержня.

Коефіцієнт зведеної довжини.

Зведеною є така довжина стержня, на якій розміщується одна напівхвиля синусоїди.

Довжини, що показано пунктиром і є звееденими.

(10)

де – коефіцієнт зведення довжини. Відтак формула Ейлера при любих закріпленнях стержня буде виглядати так:

(11)

Поняття про критичні напруження.

Графік залежності від гнучкості.

Емпірічна формула Ясинського.

Критичне напруження – це напруження, що виникає в стержні від дії на нього.

, де

Як уже відомо, виведення формули Ейлера базується на використанні ДР пружної лінії бруса. Так як область її використання знаходиться не вище

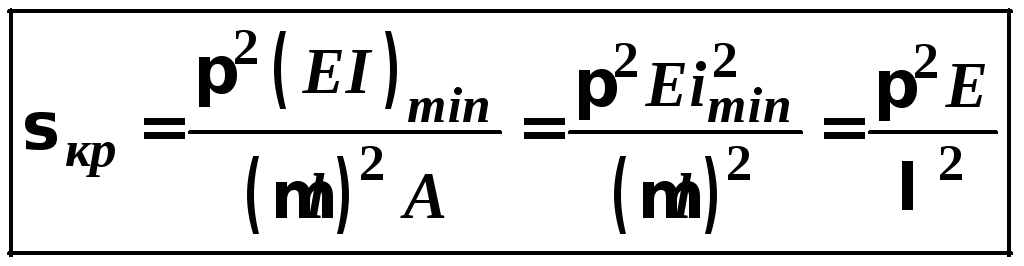, (12),

де – гнучкість стержня.– максимальна гнучкість стержня.

Гнучкість - це відношення зведеної довжини стержня до радіусу еліпса його інерції.

Визначити загрозливу гнучкість стержня за даних умов закріплення

;

;

.

Залежно від розмірів прямокутного перерізу таке його розміщення буде найраціональнішим. Раціональною конструкцією є система, у якої гнучкість в усіх площинах буде однаковою.

Повертаючись до вище сказаного, можемо констатувати, що формулою Ейлера можна користуватись тільки до тих пір, доки діюче напруження стискання не перевищує, тобто:

(12)

. (13)

Із формули (13) витікає, що границя та гранична гнучкість стержня починаючиз якої можна користуватись формулою Ейлера. Таким чином, при.

–для сталей

–для чавунів

–для дерева

Графік залежності критичних напружень від гнучкості

Формула Ясинського (15)

(16)

Коефіцієнти і – емпіричні; одиниця виміру – МПа.

Залежність (16) використовується виключно для визначення критичного напруження в чавунах.

Перша ділянка, на якій змінюється від "0" до "40" одиниць відповідає стержням малої кривизни і гнучкості. Це стержні, які ні при яких умовах не втратять стійкості і в яких визначається як при простому стиску;

Друга ділянка, на якій () змінюється від "40" до "100" одиницям для сталі, відповідає стержням середньої гнучкості. Критичні напруження визначаються тільки за формулою Ясинського;

Третя ділянка – це ділянка, на якій. Це ділянка, що відповідає стержнювеликої гнучкості. Критичні напруження визначаються для них за формулою Ейлера.

Розрахунок стиснутих стержнів на стійкість

При оцінці стійкості стиснутого стержня зустрічається два типи розрахунків:

а) перевірочний розрахунок

б) проектувальний розрахунок

Для проведення розрахунку необхідно отримати умову стійкості стиснутого стержня, аналогічну умові міцності при стиску: - при простому

стиску:

(17)

де, апри простому стиску.

Аналогічно:.

Для того, щоб поєднати івводять коефіцієнт, який називається коефіцієнтом зменшення осьового допустимого напруження при розрахунках на стійкість:

.

Він який показує в скільки разів допустиме напруження на стійкість менше. Коефіцієнтзалежить від гнучкості стержняі визначається за таблицею, маючи своє конкретне значення для кожного матеріалу.

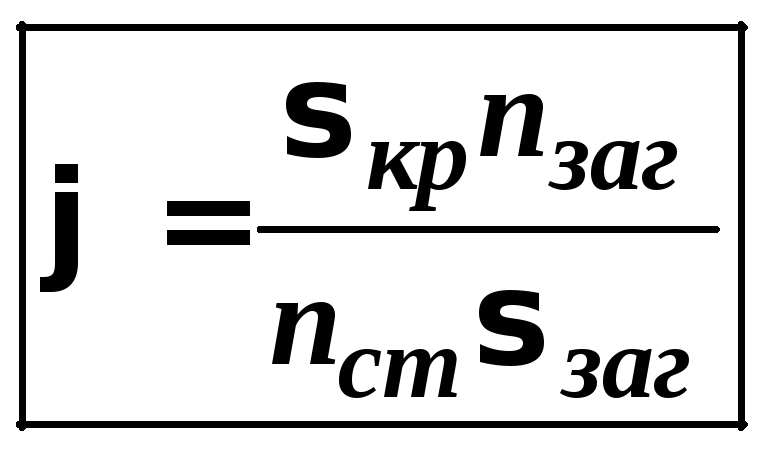(18)

1. Перевірочний розрахунок.

Перевірочні розрахунки можуть бути двох видів:

1.1. По відомим допустимим напруженням на стиск

Послідовність розрахунку:

– визначається реальне напруження на стиск, що діє в стержні, через відому величину діючого зовнішнього зусилля і площу поперечного перерізу стержня;

– ці реальні напруження порівнюють з допустимими напруженнями на стійкість, тобто аналізується умова стійкості;

(19)

– визначають через коефіцієнт;

– в свою чергу для визначення коефіцієнта необхідно визначити величину максимальної гнучкості. Потім за таблицею для даного матеріалу знаходиться коефіцієнт. Знайшовши таким чином порівнюємо його з. Якщоабо ж перевищує його на величину не більше ніж 1.5%, то умови стійкості для стержня виконуються.

1.2. За заданим допустимим коефіцієнтом стійкості

Розраховується реальний коефіцієнт стійкості. Він повинен бути:

.

– для визначення реального коефіцієнта необхідно:

.

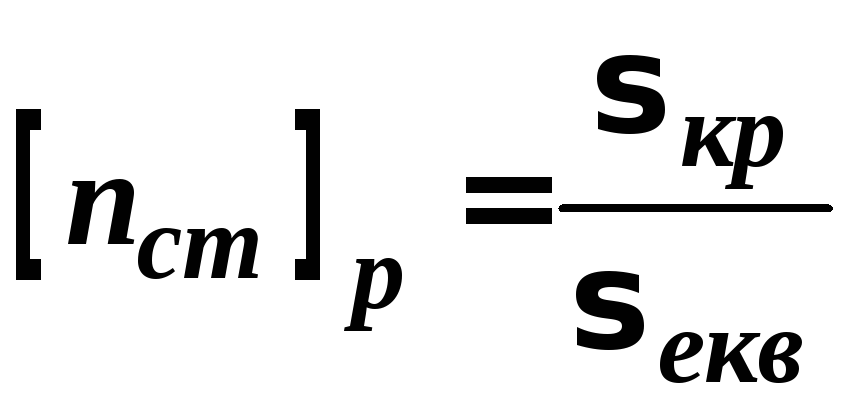– для визначення діючого напруження використовують формулу звідки, враховуючи, що, вибирають формулу для визначення

– якщо, то

– якщо, то, або ж.

2. Проектувальний розрахунок

Такий розрахунок проводиться на основі стійкості стержня:

, (1 9)

а, де величиназадана, арозраховується:

(20)

За методом послідовних наближень визначають величину.

– на першому етапі беруть рівним 0.5 чи 0.6 і підставляють у формулу (20).

.

За величиною визначають розміри поперечного перерізу;

– потім розраховують головні центральні моменти інерції і радіуси відносно головних центральних осей інерції;

– за їх значеннями визначають,;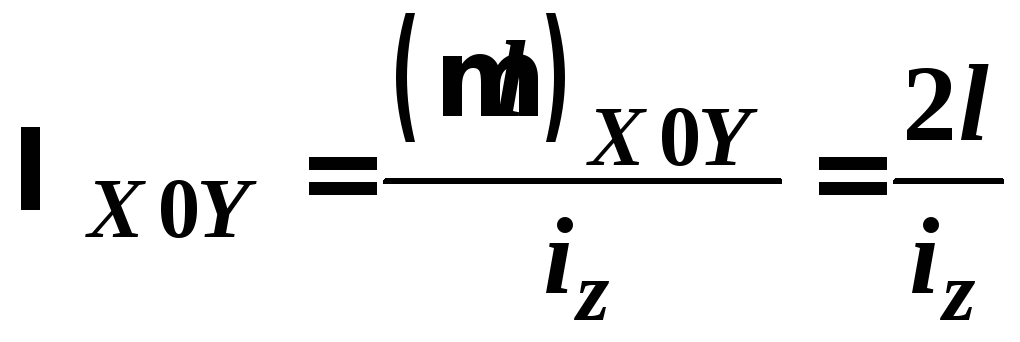

– за івибирають;

– за за таблицею, враховуючи матеріал, знаходятьза формулою:

,

де відповідає значенню, що є найближчим меншим доу таблиці;

відповідає значенню, що є найближчим більшим доу таблиці;

– найближче менше дозначення у таблиці.

Далі підставляють у формулу (20) тепер уже. Якщотана величину не більше 5%, або жна величину до 1.5%, то це напруження, а відповідно і коефіцієнтзалишають.

У противному разі, робиться наступне наближення коефіцієнта за формулою

Самостійно: (Писаренко ст. 507 - 508.) Про вибір матеріалу і раціональних форм поперечних перерізів для стиснутих стержнів.